以下、高周波に於ける伝送線路のパラメータ測定を考えますが、 高周波のケーブルの電気特性は非常に簡単で、 下記が成り立ちます。 v, Z0 は近似式ですが、極めて高い精度で成り立ちます。
v = 1/sqrt(L*C) (1) Z0 = sqrt(L/C) (2) β = ω/v (3) ここに、 v = ケーブルを伝搬する電磁波の位相速度 (m/s) = f*λ (4) Z0 = 特性インピーダンス (Ω) L = 伝送線路の単位長あたりインダクタンス (H/m) C = 伝送線路の単位長あたりキャパシタンス (F/m) Vr = 速度係数 (0 < Vr <= 1) = v/c (5) c = 299792458 (真空中の光速 m/s) γ = 伝搬定数 = α + j*β α = 減衰定数 (neper/m) β = 位相定数 (rad/m) ω = 角周波数 (rad/s) = 2*π*f f = 周波数 (Hz) λ = ケーブルを伝搬する電磁波の波長 (m)また、銅導体と高周波特性の良い誘電体で作られた高周波ケーブルでは 下記が成り立ちます。
α = a1 * sqrt(f) + a2 * f (6) ここに、 a1 = 導体構造と導電率で決まる定数 a2 = 誘電体構造と誘電体損率で決まる定数減衰の起因は導体中のジュール熱による発熱と、 電子レンジなどに応用される誘電体中の分子振動による発熱にありますが、 前者は表皮効果より周波数の平方根に比例し、 後者は ω*C*D ですから周波数に比例することになります。
ただ、ポリエチレンなど優れた誘電材料だと、 1 GHz 以上まで表皮効果による損失が圧倒的に大きく、 誘電体損失は無視できるのが普通です。
同調法(resonant method)では open-short 法の障害となる共振を積極的に利用します。 インピーダンス Zt で終端した伝送線路の入力インピーダンスは
Zin = (Zt/Z0 + tanh(γ*l)) / (1 + (Zt/Z0)*tanh(γ*l)) (7) ここに、 Zin = 伝送線路の入力インピーダンス (Ω) Zt = 伝送線路の終端インピーダンス (Ω)ですから、終端短絡線路と終端開放線路なら、それぞれ
Zsc = Z0*tanh(γ*l) Zoc = Z0/tanh(γ*l) γ = α + j*β β = ω/v tanh(γ*l) = tanh(α*l+j*β*l) = (tanh(α*l)+j*tan(β*l))/(1+j*tanh(α*l)tan(β*l)) ここに、 Zsc = 終端短絡線路のインピーダンス Zoc = 終端開放線路のインピーダンスですから、n = 0, 1, 2, .. として
Zsc は β = π/4*(2*n+1) で極大 1/tanh(α*l) (8)
β = π/4*(2*n) で極小 tanh(α*l) (9)
Zoc は β = π/4*(2*n+1) で極小 tanh(α*l) (8)
β = π/4*(2*n) で極大 1/tanh(α*l) (9)
となる(入力インピーダンス絶対値の)周期的変化をします。
極値から減衰定数が得られることに注意してください。
極値が純抵抗ですから、
インピーダンスアナライザで同調周波数を求める場合は、
リアクタンス分(偏角)が 0 になる周波数を二分法で探します。
絶対値しか得られないときは、
黄金分割法を使って極大、極小値を探します。
(注1)
この入力インピーダンスの周期的変化はネットワークアナライザ(VNA - Vector Network Anlyzer) による測定でよく見られる波打ちの原因で、 不勉強な技術者だと自分の測定ミスに気づかず、 試料の特性が悪いと思い込む陥穴の一つになりますが、 同調法ではこの入力インピーダンスが極大と極小になる周波数の測定値から出発します。
周波数測定は電気計測の中では極めて高い精度が容易に得られるのが特徴で、 その結果、同調法によるケーブルの測定も精度の高いものになりますが、 もう一つの利点は、open-short 法に於ける大きな誤差要因である、 試料の入力側浮遊インピーダンス、 終端側の浮遊インピーダンスの影響が少なく、 終端短絡試料と終端開放試料の長さの違いによる誤差を排除できることです。
共振周波数の測定にはインピーダンスアナライザ(impedance analzer) やネットワークアナライザ(Network Analyzer) のような現代の本格的試験機以外に、 古くからアマチュア無線で使われてきたディップメータ(dipmeter)や 古典的計測器のQメータ(Q meter)、 あるいは基本的計測機器である発信器と電圧計や オシロスコープ(Oscilloscope)の組み合わせなど、 多様な機器が使えます。 ディップメータや Qメータは今では市販品がなくなってしまいましたが、 極めて応用範囲の広いツールで、 平衡ケーブルでも使えるとか捨てがたいところがあります。
最も試料作成の容易な終端開放ケーブルの入力インピーダンスはケーブルの長さが 1/4 波長、3/4 波長、5/4 波長 .. で極小になりますが、 入力インピーダンスが極小になる周波数間隔は 1/2 波長ですから、 (4) 式を考慮して、 ケーブルの長さがわかればケーブルを伝わる電磁波の位相速度がわかって、 下記のようになります。
v = 2 * l * Δf (10) ここに、 v = ケーブルを伝わる電磁波の位相速度 (m/s) l = ケーブルの長さ (m) Δf = 共振周波数間隔 (Hz)つまり、電磁波の速度測定は実に簡単です。
共振周波数は 入力インピーダンスが極小になる場合と極大になる場合の二種類がありますが、 同種の共振周波数の差なら、どちらでもかまいません。 多くの計測器では極小値を使いますが、 Q メータの場合は極大値を使いますし、 インピーダンスアナライザの場合は偏角 0 の周波数を使うことになります。
速度係数は
Vr = v / c ここに、 Vr = 速度係数 (0 < Vr <= 1) c = 299792458 (真空中の光速 m/s)
になりますが、 周波数が低い場合は導体の内部インダクタンスが無視できず、 電磁波の位相速度が少し小さくなりますが、 1 MHz 以上になると、ほぼ一定になり、Δf も実用誤差の範囲内で一定になります。 逆に見れば、 Δf が一定していれば電磁波の位相速度も周波数に依存しないことになります。
(1), (2) 式から L を消去して
Z0 = 1/(v*C) (11)ですから、あとはキャパシタンスがわかれば特性インピーダンスがわかります。
高周波に於けるキャパシタンス測定は難しいのですが、 ポリエチレンなどの周波数特性の優れた誘電体であれば、 1 KHz から 100 kHz 程度の低周波で測定した値が GHz 帯域まで使える ことがわかっていますので、低周波に於ける測定値を使うことができますし、 インピーダンス測定機の測定可能な最低周波数が 1 MHz までしかないという場合は、 1 MHz から 1/4 波長の 80 % 程度までの周波数で 1 MHz 刻で測定した 入力インピーダンスから 低周波に於ける一次定数測定 で解説した分布定数補正係数 (β*l)/tan(β*l) を求め、 それを使って正しい値を決定することができます。 (注2)
インピーダンスアナライザのようにインピーダンス測定が可能な場合は、 (8), (9) により同調点のインピーダンスから
α = atanh(Z_min / Z0) / l
= 1 / (acoth(Z_max / Z0) * 1)
ここに、
Z_min = 終端開放または終端短絡線路の入力インピーダンスの極小値 (Ω)
Z_max = 終端開放または終端短絡線路の入力インピーダンスの極大値 (Ω)
α = Z_min の周波数における減衰定数 (neper/m)
Z0 = 試料の特性インピーダンス (Ω)
l = 試料長 (m)
で同調周波数に於ける減衰定数が得られます。
Z_min と Z_max は純抵抗であることに注意してください。
Z_max を使うよりZ_min を使うほうが高い精度が得られますが、
理由は同調点近くの入力インピーダンスの周波数による変化が
Z_max で極めて大きいため、測定誤差も大きくなるためです。
試料としては終端開放線路、終端短絡線路のいずれも使えますが、
より低い周波数まで測定できるのと、作成が簡単な点で終端開放線路に利点があります。
open-short法のように任意の周波数について測定できるわけではありませんが、 誘電体損失の少ない高周波のケーブルは 減衰定数が周波数の平方根に比例することがわかっていますから、 途中の周波数については補間できます。 また、測定したい周波数で共振する試料の長さを選べば、 事実上任意の周波数で測定できますが、 通常は得られた離散的測定値に (6) 式を 当てはめて、 係数 a, b を重回帰分析で求めれば充分です。
インピーダンスアナライザのようなベクトル測定ができず、 電圧計でインピーダンスに比例した電圧を読むとか Q メータのように、インピーダンスの絶対値しか得られない場合は 共振の鋭さから減衰定数がわかります。

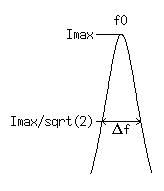
1図 共振の鋭さから減衰定数を求める
例えば、 ケーブルの始端に発信器とケーブルの特性インピーダンスより十分大きな 入力インピーダンスを持つ電圧計を接続し、 電流が最大になる中心周波数 f0 を探し、 次ぎにその中心周波数から上下に少し離れた周波数で、 ピーク電流の 1/sqrt(2) になる周波数 f1, f2 を見出し、 下記で中心周波数に於ける減衰定数を求めます。
α = π*Δf/v ここに、 α = 減衰定数 (neper/m) Δf = f2 - f1 (半電力周波数差 Hz)この方法はQ メータで古くから使われてきた手法と原理的に同じです。 (注3)
なお、ここでは同調法の伝送線路定数測定への応用に限定して解説しましたが、 複数の伝送線路の電気長を正確に合わせる場合とか、 いろいろな用途があって、 DipmeterとかQ-meterはこういった幅の広い用途を考慮した 設計になっています。
高周波の特性インピーダンスを求める方法として最も簡単なのは TDR(Time Domain Reflectmetry)です。 TDRは立上りの早いステップ電圧を試料に印加し、 試料の両端の電圧波形を広帯域オシロスコープで観測することで 試料のステップ応答を見ますが、 試料が伝送線路の場合は、 試料始端に於ける反射波の大きさから試料の特性インピーダンスが得られます。
Z0/Zs = (1 + r)/(1 - r) (12) ここに、 Zs = TDRのステップジェネレータ出力インピーダンス (通常 50Ω) r = 反射係数 = 反射波の電圧/入射波の電圧 (0 < r < 1)(注4)
TDR専用機では r や Z0 が直読できるようになっているのが普通ですが、 長いケーブルを扱う場合は、ケーブル始端以外では正しい Z0 は得られません。 (注5)
位相速度は 試料始端からの反射波と試料終端からの反射波の時間差から求めるkとができて、 TDR専用器の場合は直読できるように設計されています。
v = 2*l/Td ここに、 v = 試料を伝わる電磁波の位相速度 (m/s) l = 試料の長さ (m) Td = 試料始端からの反射波と試料終端からの反射波の時間差 (s)
TDRのマニュアルや解説書には書かれていませんが、 反射波の波形は試料の始端から終端までの往復分の減衰を受けていますから、 反射波の波形から試料の減衰を求めることができます。
反射波の波形とステップ波形のフーリエ変換から減衰を求めることもできますが、 Levenberg-Marquardt Methodなどの非線形最小二乗法で、 高周波ケーブルの理論的ステップ応答波形
h(t) = A * (1 - erf(B / sqrt(t - t0)) + C (t0 =< t)
= 0 (t < t0)
ここに、
h(t) = ステップ応答の電圧波形 (V)
t = 時間 (s)
erf(x) = 誤差関数
t0 = ステップ応答の先頭時間 (s)
A, B, C = 定数
を実測波形にあてはめ、
α = 2*sqrt(π*f)*B/l ここに、 α = 減衰定数 (neper/m) f = 周波数 (Hz) l - 試料の長さ (m)で減衰を求めることができます。
実際の計算ではgnuplotを使うと簡単ですが、 初期値をうまく選ばないと収束しないことがあります。
さらに簡単な方法としては、 ステップ波形の 50 % 立上り時間から、
erf((l/(2*sqrt(π*t))) * (α/sqrt(f))) = 0.5 ここに、 t = ステップ応答の50 % 立上り時間 (s) なお、 erf(0.476936..) = 0.5を解いて、α/sqrt(f) を求めることもできます。 非線形方程式ですから数値計算で解きますが、導体が軟銅なら
t50 = 0.35*(α*l)^2/f ここに、 t50 = ステップ応答の50 % 立上り時間 (s)になります。
TDR専用機は高価ですが、 10 m から数 10 m の試料を使ってケーブルの特性を認めるのであれば 高い分解能は要りませんから、 安価な方形波発信器(Function Generator)と安価なオシロスコープを使って、 オシロスコープの入力端子に BNC の T 分岐を付け、片側に発信器、 他の側に試料を接続したセットで充分間に合います。 一度は、こういったことをやっておくとTDRの原理が よくわかると思います。
50 % 立上時間を使う方法については パルスの立上り時間とケーブルの長さの関係 もご蘭ください。
ネットワークアナライザ (VNA - Vector Network Analyzer) は試料のS-parameterを求める装置ですが、
Z0 = Zs*sqrt((1+S11)^2-S21^2)/((1-S11)^2-S21^2)) γ*l = ((1+S11)^2-S21^2)*((a-S11)^2-S21^2)/(2*S21)^2 ここに、 Zs = 50 .. ネットワークアナライザのシステムインピーダンス l = ケーブルの長さ (m)で、二次定数を求めることができます。 (注7) ただし、 試料の長さが測定波長の 1/2 の整数倍のときは、 試料の入力インピーダンスが VNA のシステムインピーダンスと等しくなって、 Z0 の値は不定になりますから、 特性インピーダンスの測定はできないことに注意が必要です。
ケーブルの反射が小さくて S11 〜 S22 << 1 なら
Z0 〜 (1 + S11)/(1 - S11)*sqrt(Z1*Z2) 〜 (1 + S11)/(1 - S11)*Zs S21 〜 exp(-γ*l)ですから、Z0 の測定では S11 の誤差が拡大されて、 open-short 法に於ける困難が再現されます。 この誤差が小さくなるのはケーブルの電気長が半波長の整数倍のときで、 この場合、ケーブルの入力インピーダンスは
Zin = (Zs/Z0 + tanh(α*l))/(1 + Zs/Z0*tanh(α*l))ですから、ケーブルが長いか周波数が高くて 1 << α*l なら、
Z0 〜 Zinケーブル長が短いか周波数が低くて α*l << 1 なら
Z0 〜 Zin*Zsになって、反射の影響がなくなりますが、 最も安全な方法は試料端での反射を避けるか、逆に反射を最大限利用して、
Z0 は試料の 1/4 波長の奇数倍の周波数で測定する 減衰定数は試料の 1/2 波長の整数倍の周波数で測定することで、この場合、試料の特性インピーダンスは
Z0 = sqrt((1 + S11) / (1 - S11)) * Zs減衰定数は
α = S21で得られます。 ネットワークアナライザの S21 が dB 表示の場合は
log(10) / 20倍 (* 0.115) して neper 単位に変換します。
S21 については Z0 のように、誤差の拡大による不安定さはありませんから、 測定は容易です。
この他、 S21の波打ちがなくなるようにシステムインピーダンスを変換 し、変換したシステムインピーダンスから Z0 を求め、 変換した S12 から減衰定数を求めるといった方法もあります。 (注8)
位相速度はS21の位相の周波数特性と (3) 式から計算できますが、 測定器の表示は 2*π*n (n = 0, 1, 2, ..) を引いた値ですから、 誘電体の誘電率と試料の長さから概算した値から n を推測するといった処理が 必要です。
ネットワークアナライザを使った二次定数測定については Sパラメータの基礎を御覧ください。 また、フーリエ変換と線形システムの基礎 (1) - 解説 もお役にたつかもしれません。
VSWR bridgeは3辺を高周波まで使える純抵抗 R、 残り1辺を試料」に接続して、 アンバランスを測定するもので、 VSWR (Voltage Standing Wave Ratio)を高精度で測れますので、 VSWR から反射係数を求め、 そこから特性インピーダンスを計算することができます。
VSWR bridge には トラッキングジェネレータ付きスペクトラムアナライザと組み合わせて VSWR の周波数特性を見るとか、 いろいろな用途がありますが、 今の時代だと汎用測定部品とは言えないと思いますので、 興味を持たれたかたは他の資料を調べてください。
この他にも、実にたくさんの測定法があって、 高価な計測機器がなくても、できることはたくさんあります。
多量の計算をするわけではありませんし、測定には時間がかかりますから、 簡単なアルゴリズムが適しています。
いずれのプログラムも変数(周波数)は正の値であると仮定しています。 2分法は原始的ですが 2 の巾乗で精度が上がるため効率はよいです。 黄金分割法は測定回数を減らす工夫です。 実用化する場合は範囲の妥当正などをチェックするコードを追加するほうが よいと思います。 プログラム例の日本語文字コードは EUC です。ポリエチレンやテフロンの誘電率が低周波から高周波までの広い周波数にわたって 変化しないことは材料自体の電気特性測定により確認できますが、 同調法による共振周波数差が一定していることから L*C の値が一定していることがわかり、 L の値が導体の表皮効果により周波数による変化のない外部インダクタンスのみ で決まることが古典物理学の最高峰である電磁気学(Electro_magnetic Theory) によって保証されますから、 結局 C も周波数に関係なく一定値になることがわかります。同様に、 低周波測定の広域側限界でのインダクタンスも高周波領域に演繹できることが わかります。
従って、キャパシタンスの値は共振周波数から充分離れた、 例えば、100 kHz とか 1 MHz で測定すればよいのですが、 インピーダンス測定器で測定可能な周波数が 1 MHz 程度で、 低域の測定誤差が大きい場合は、 1 MHz から共振周波数の 80 % 程度の周波数まで、 1 MHz 間隔で終端開放線路の入力インピーダンスを測定し、 次式で計算する c の値が周波数に依存せず一定になるような (β*l) を探し、 キャパシタンスを決定することができます。
c = cm * (β*l) / tan(β*l) cm = -y / ω / (x * x + y * y) ここに、 cm = 終端開放線路のキャパシタンス測定値 (F/m) c = 終端開放線路のキャパシタンス補正値 (F/m) x + j * y = 終端開放線路の入力インピーダンス j = sqrt(-1) ω = 各周波数 (rad/s) = 2 * π * f f = 周波数 (Hz) β = 位相定数 (rad/m) = ω / (c * Vr) l = 試料の長さ (m) Vr = 速度係数 c = 2.99792458e8 (真空中の光速)真の(β*l) を探す方法としては、 周波数の関数としての c に「c = b」(b は定数)の回帰直線をあてはめて 誤差分散が極小になる (β*l) を求めるとか、 「c = a * f + b」i(a, b は定数)の回帰直線をあてはめて、 誤差分散が極小になるか、a = 0 になる (β*l) を求めるのが簡単です。 極小値を探す場合は黄金分割法が良いでしょう。 a = 0 を探すときは2分法で間に合います。
発信器に終端開放線路ないし終端短絡端線路を接続し、 接続点に入力インピーダンスの大きい電圧計を接続した測定系を考えます。 周波数を可変して電圧計の振れが最小になる周波数の近くでは 線路の入力インピーダンスは発信器の出力インピーダンスより十分小さいため、 測定器の出力インピーダンスと電圧計の表示値から線路に流れる電流がわかります。
発信器の周波数を変えて電圧計の表示値が最小になる周波数を f0、 そのときの電流を i0 として、 周波数を少し上げで電流が i0/sqrt(2) になる周波数を f2、 周波数を少し下げて電流が i0/sqrt(2) になる周波数を f1 とすると、
Zf0 = tanh(α*l) Zf2 = (tanh(α2*l)+j*tan(β2*l)/(1+j*tanh(α2*l)*tan(β2*l)) Zf2 = (tanh(α1*l)+j*tan(β1*l)/(1+j*tanh(α1*l)*tan(β1*l)) ここに、 Zf0 = 周波数 f0 に於ける線路の入力インピーダンス (Ω) Zf2 = 周波数 f2 に於ける線路の入力インピーダンス (Ω) Zf1 = 周波数 f1 に於ける線路の入力インピーダンス (Ω) α2 = 周波数 f2 に於ける線路の減衰定数 (neper/m) α1 = 周波数 f1 に於ける線路の減衰定数 (neper/m) β2 = 周波数 f2 に於ける線路の位相定数 (rad/m) β1 = 周波数 f1 に於ける線路の位相定数 (rad/m) l = 線路の長さ (m)になりますが、α*l << 1 なら f0, f1, f2 の差は僅かですから、 α〜α1〜α2、-β1〜β2 << 1 が成り立ち
abs(Zf2) = sqrt(2)*Zf0 abs(Zf1) = sqrt(2)*Zf0になります。従って
abs(tanh(α*l)+j*tan(β*l))/(1+j*tanh(α*l)*tan(β*l)) = sqr(2)*tanh(α*l)から
tan(β*l) = tanh(α*l)β*l << 1、α*l << 1 なら
+-β = αβ = ω/v, ω = 2*π*f を考慮すれば
α 〜 π*(f2-f1)/vが得られます。
特性インピーダンス Z0 の線路に負荷インピーダンス Zt を接続したとき、 反射係数 r は
r = (Zt - Z0)/(Zt + Z0)ですから、Z0 -> Zs, Zt -> Z0 で置き換えれば (12) 式が得られます。
5.5. 注5 - TDRによるケーブルの特性インピーダンス測定の注意
TDRのマニュアルや解説書を見ると、 試料の特性インピーダンスを測定しているように書いてありますが、 実際には試料の入力インピーダスの時間領域測定です。 プリント基板のようなサイズの小さな部品や短いケーブルなら大きな違いは出ませんが、 長いケーブルの場合は眼に見える違いを生じます。 例えば、 TDR によるケーブル測定の謎を見てください。
高周波ケーブルのステップ応答は下記で計算できます。
h(t) = 1 - erf(l*K/(4*R0*√t))
ここに、
t = 時間 (s)
R0 = 高周波の特性インピーダンス (Ω)
erf(x) = 誤差関数
x
= (2/√π)*∫e^(-t^2)*dt (10)
0
K = (1/(2*π*a)*√(μ/σ)
= 2.34e-8/a .. 電気銅導体の場合
a = 導体半径 (m)
μ = 導体の透磁率 (H/m) .. 軟銅なら 4e-7*π
σ = 導体の導電率 (S/m) .. 軟銅なら 5.80e7
σ = 導体の導電率 (S/m) .. 軟銅なら 5.80e7
導体半径は往復導体の損失を考慮した等価的な値を使います。
この式は
R.L.Wigington, N.S.Nahman,- Transient Analysis of Coaxial Cables
(Proc. IRE, pp 166-174, Feb 1957)
によります。
また、パルスの立上り時間とケーブルの長さの関係
でもこの問題に触れています。
Fパラメータ(四端子行列)とSパラメータの関係
Z0^2/Z1/Z2 = ((1+S11)*(1+S22)-S21*S12)/((1-S11)*(1-S22)-S21*S12) (sinh(γ*l))^2*Z1/Z2 = ((1+S11)*(1+S22)-S21*S12)*((1-S11)*(1-S22)-S21*S12) /(2*S21)^2 ネットワークアナライザの場合は Z1 = Z2 = 50 (映像用では 75 もある)とケーブルのFパラメータ
A = cosh(γ*l) B = Z0*sinh(γ*l) C= (1/Z0)*sinh(γ*l) D = cosh(γ*l)から得られます。
ケーブルのFパラメータについては
伝送線路理論の基礎
Fパラメータ(四端子行列)とSパラメータの関係については
を御覧ください。
ネットワークアナライザのシステムインピーダンスは 50 Ωが普通ですが、
他のシステムインピーダンスに変換する場合は、一旦
S パラメータをシステムインピーダンスに依存しない
F パラメータに変換してから、
目的とする他のシステムインピーダンスのS パラメータに変換します。
こういった変換については
Sパラメータの基礎をご覧ください。
この方法を利用して、
ネットワークアナライザで測定した S11 や S21 の波打ちがなくなるような
システムインピーダンスを探す方法で、
ネットワークアナライザでは苦手な特性インピーダンスを求めることもできます。
平林浩一, 2016-03-23
5.8. 注8 - S パラメータのシステムインピーダンス変換