ケーブルの二次定数測定 (4) - 平衡ケーブル測定

1. 平衡ケーブル特有の注意点

伝送ケーブルには同軸ケーブルのような 不平衡ケーブル(unbalanced cable)と、 LAN ケーブルのような 平衡ケーブル(blanced cable)の二種類があります。平衡というのは回路の個々の導体と大地ないしシールド間インピーダンスが等しいという意味ですが、この対地インピーダンスというのは通常キャパシタンスです。

一方、電子計測機器のほとんどは不平衡で、測定端子のいずれかが接地されています。

不平衡の電子計測機器で平衡ケーブルを測定すると、往復２導体間のインピーダンスと接地側でない導体の対地インピーダンスの並列回路を測定することになって、正しい値が得られません。

つまり、平衡ケーブルの測定では

Balunで平衡ケーブルを不平衡に変換してから不平衡計測機器で測定する
平衡型の計測機器を使う

のいずれかにしなければなりません。 Balun(バラン)は Balance と Unbalunce の合成語です。

2. Balun

平衡-不平衡変換を行うための代表的なBalunはトランス(electric transformer)ですが、伝送線路の位相差を利用したものとか、いろいろな種類があって、多くの場合 1:2 あるいは 1:4 の変圧比になります。

いずれも広帯域を得るのが困難で、高い周波数まで使えるものを作るのは至難の技です。入手可能な製品としては日本ではほとんど知られていませんが、 North Hills社の NH16447 が 5-1.2GHz という広い帯域幅を実現しています。この他PRODYN社の Balun にも高い周波数で使えるものがあります。

さらに高い周波数では、帯域が狭くなりますが、同軸ケーブルを使った1/2 波長バランの自作が良い選択です。

１図 1/2 波長バラン

1/2 波長バランは電気長 1/2 波長の同軸ケーブルを U 字型に曲げ、その一端の内部導体を任意の長さの同じ同軸ケーブルの一端の内部導体に接続したもので、 U 字型同軸ケーブルの両端と U 字型に接続した同軸ケーブルの外部導体外部導体は密着させて接続します。導線を何回か巻き付けて半田付けすると確実です。 U 字型でない同軸ケーブルの長さは自由です。

U 字型同軸ケーブルの長さが 1/2 波長だと両端の電流が逆方向になりますから、極めて正確な平衡伝送になりますが、そのインピーダンスは不平衡側のインピーダンスの 4 倍になります。また、トランスに比べれば帯域が狭くなりますので、測定帯域が広い場合は複数の 1/2 波長バランを用意することになります。

10 MHz 以下とか 100 MHz 程度までの低い周波数なら、トランス型BALUNの入手は用意で、自作も難しくはありません。

3. 平衡型の計測機器

特定分野の測定に特化した製品を除けば、市販の平衡型の計測機器はほとんどなくなって、かつては多量に使われていた Dip-meterやQ-meterも自作しかなくなってしました。測定に多少手間がかかりますが、他の測定機では得られない利点があって、できれば一つは用意しておきたいものの一つです。

完全な平衡型ではありませんが、 オペアンプ(OP Amp)の仮想接地機能を使った 自動平衡ブリッジ(automatic balance bridge)と呼ばれるインピーダンス測定器は短い平衡ケーブルでも誤差が少なく、使いやすいです。

4. BALUNの校正

インピーダンス測定機と試料の間にBALUNを挿入すると、正しい試料のインピーダンスが得られなくなりますが、この対策は二つあります。

インピーダンス測定機にBALUNを接続した状態で測定機を校正する
BALUNの影響を除去するための補正データを作っておく

いずれにしても、平衡型の標準試料が必要ですが、通常はOpen(インピーダンス無限大)、(インピーダンス 0)、 Load(通常 100Ω)の３つを用意します。

平衡型の標準試料の市販品はありませんので、自作するのが普通ですが、 Loadについては高周波特性の良い小型抵抗をたくさん購入して選別するか、 BALUNの校正データを用意する場合は、正確な抵抗値を測定して、その値をLoadとして使います。

インピーダンス測定機にBALUNを接続した状態で測定機を校正する場合は、平衡型の標準試料を使ってインピーダンス測定機に内蔵された校正操作をすれば済みますので、ここでは測定機に付属する標準試料を使って測定機は不平衡で校正したインピーダンス測定機で BALUNの校正データを作成する方法を解説します。

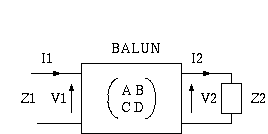
２図 BALUNの校正

２図のようにBALUNを４端子回路として見たとき、出力側にインピーダンス Zl の負荷を接続し、 Zl にOpen、Short、Loadの３つの標準試料を接続したときの BALUN入力側インピーダンス、 Zs, Zo, Zl を測定し、次ぎに Zl として未知インピーダンス Zx を接続したときの入力インピーダンスを Zm とすれば

  Zx = (1-Zo/Zl)/(1-Zm/Zo)*(Zm-Zs)/(Zl-Zs)*Zstd
  ここに、
	Zx = 未知インピーダンスの値
	Zo = の出力側ににOpen標準を接続したときの入力インピーダンス
	Zs = の出力側ににShort標準を接続したときの入力インピーダンス
	Zl = の出力側ににLoad標準を接続したときの入力インピーダンス
	Zstd = Load標準のインピーダンス

で未知インピーダンスの値がわかります。 (注１)

この校正はBALUN以外の任意の回路で使えますので、自作治具の校正にも利用できます。

Z0, Zs, Zl の値は周波数によって変わりますから、必要な周波数帯域で必要な精度の補間ができるだけの数だけ必要ですが、 BALUNとLoad標準に固有の値ですから、一度測定しておけば済みますので、校正データファイルとして格納し、次回からは測定開始時にそれを読み出して使うようにプログラミングするのが普通です。

5. TDRによる平衡ケーブル測定

TDRで平衡ケーブルを測定する場合は立上りの速いパルスに対応できるような広帯域のBALUNが存在しないため、平衡型ステップジェネレータと２チャンネルのオシロスコープを使うのが普通で、この場合は差動モード(differential mode)と コモンモード(common mode) の特性インピーダンスや速度係数、減衰を同時に求めることができます。

TDRだと高い精度は得られませんが、手軽で測定ミスが少ないのが利点で、使える環境があれば、他の測定法で得られた値の検証に使う習慣をつかるのが良いと思います。

6. ネットワークアナライザによる平衡ケーブル測定

ネットワークアナライザの場合は２つの測定ポートに各１個のBALUNを接続した状態で校正すれば平衡ケーブルの測定ができますが、測定周波数と帯域が広い場合は４ポートのネットワークアナライザを使うのが普通です。

２ポートのネットワークアナライザしかない場合は、測定機に接続しない試料端はすべて 50Ωで終端した状態で、すべての２ポートの組み合わせについて、Ｓパラメータを測定し、次式ですべてもモードに対するＳパラメータを計算します。 50Ωの終端抵抗はネットワークアナライザの校正用標準が使えます。

            | Sdd11  Sdd12 |   | S11-S12-S21+S22  S13-S14-S23+S24 |
  2 * Sdd = |              | = |                                  |
            | Sdd21  Sdd22 |   | S31-S32-S41+S42  S33-S34-S43+S44 |

            | Sdc11  Sdc12 |   | S11+S12-S21-S22  S13+S14-S23-S24 |
  2 * Sdc = |              | = |                                  |
            | Sdc21  Sdc22 |   | S31+S32-S41-S42  S33+S34-S43-S44 |

            | Scd11  Scd12 |   | S11-S12+S21-S22  S13-S14+S23-S24 |
  2 * Scd = |              | = |                                  |
            | Scd21  Scd22 |   | S31-S32+S41-S42  S33-S34+S43-S44 |

            | Scc11  Scc12 |   | S11+S12+S21+S22  S13+S14+S23+S24 |
  2 * Scc = |              | = |                                  |
            | Scc21  Scc22 |   | S31+S32+S41+S42  S33+S34+S43+S44 |

Sdd は両端が差動(differential)モードの場合、つまり、通常の平衡伝送で使うときのＳパラメータ、 Scc は両端がコモン(common)モードの場合のＳパラメータ、 Sdc と Scd は片端が差動モードで他の端がコモンモードで使うときのＳパラメータです。 Sdc と Scd を意図的に使うことはありませんが、意図しないノイズ経路などでできてしまうのが普通です。

Sdd からケーブルの二次定数を計算する方法は不平衡試料の場合と同じです。

２ポートのネットワーックアナライザだと６回の測定が必要ですから、かなりの手間がかかるわけで、絶えず測定しなければならない場合は４ポートのネットワークアナライザに投資するほうが良いと思います。

7. 注

7.1. 注１４端子回路網で記述可能な治具の補正

２図のを４端子回路網と見ると

  V1 = A*V2 + B*I2
  I1 = C*V2 + D*I2
  Z1 = V1/I1
  Z2 = V2/I2

から

  Zs =B/D                                 (a1)
  Zo = A/C                                (a2)
  Zl = (A*Zstd + B)/(C*Zstd + D)          (a3)
  Zm = (A*Zx + B)/(C*Zx + D)              (a4)

(a3) から

  Zl = (Zstd + B/A)/(Zstd _ D/C)*(A/C)
     = (Zstd + B/A)/(Zstd + B*Zo/(A*Zs))*Zo
  B/A = Zs*(Zo - Zl)/(Zo*(Zl - Zs)*Zstd
  D/C = (B/A)*(Zo/Zs) = (Zo - Zl)/(Zl - Zs)*Zstd

(a5) から

  Zx = (B - Zm*D)/(Zm*C - A) = (B/D - Zm)/(Zm - A/C)*(D/C)
     = (Zs - Zm0)/(Zm - Zo)*(D/C)
     = (Zo - Zl)/(Zo - Zm)*(Zm - Zs)/(Zl - Zs)*Zstd
     = (1 - Zl/Zo)/(1 - Zm/Zo)*(Zm - Zs)/(Zl - Zs)*Zstd

Zm,Zl >> Zs, Zm,Zs << Zo なら Zx ～ Zm/Zl*Zstd になります。この結果は A*D - B*C = 1 という自然回路条件を使っていませんから、任意の回路について成立します。

平林浩一, 2016-03-25