薄肉円筒導体内部の線電流による渦電流損失を誘導限となる線電流から見た 等価抵抗(equivalent resistance)と 薄肉円筒内部の電流分布を計算してみます。
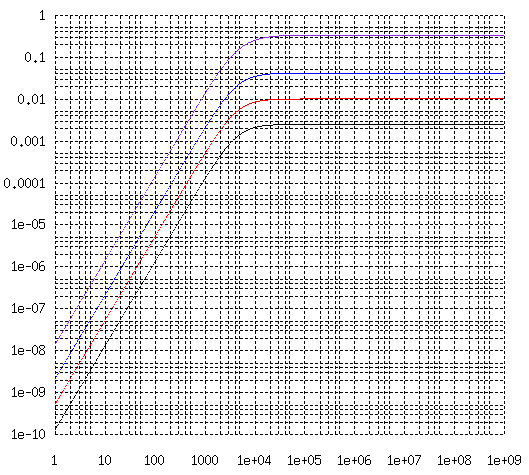
近接導体の渦電流問題 - 導体の渦電流問題 (6) の (2) 式 Rac/Rdc を 半径 a=5 mm 厚さ t=0.1 mm の円筒で、 s/a = 0.05 (黒), 0.10 (赤), 0.20 (青), 0.50 (紫) について計算した結果は下記のようになります。 横軸は周波数 (Hz) です。

1図 薄肉円筒導体内部の線電流による渦電流損失 Re(f)
内部線電流による薄肉円筒の渦電流による等価抵抗(equivalent registance)は 周波数が低いうちは周波数に自乗に比例して増えますが、 周波数が高くなると一定値になることと、 (s/a)^2 に比例することに注意してください。
周波数が低いうちは表皮効果と区別がつかず、 周波数が高くなると周波数特性のない損失、 つまり、直流抵抗が少し増えたように見えるということで、 伝送波形に大きな歪みを与える要因ではなくなります。
この曲線の意味は横軸を表皮深さで規格化した円筒の厚さ t/δ に変換するとよくわかります。
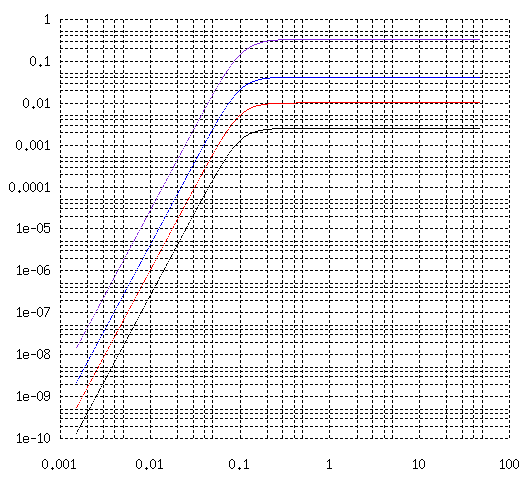
2図 薄肉円筒導体内部の線電流による渦電流損失 Re(t/δ)
侵入の深さに対して円筒の厚さが十分大きいときは、 円筒に流れる渦電流が線電流の大きさに比例しますから、 損失はその自乗に比例することになります。
しかし、円筒の厚さが侵入の深さに近付くにつれて、 円筒内部に電磁波が侵入できなくなって、 円筒内部の渦電流損失も極限値に収束します。
近接導体の渦電流問題 - 導体の渦電流問題 (5) の (1) 式 i(θ) を s/a = 0.05 (黒), 0.10 (赤), 0.20 (青), 0.50 (紫) について計算した結果は下記のようになります。
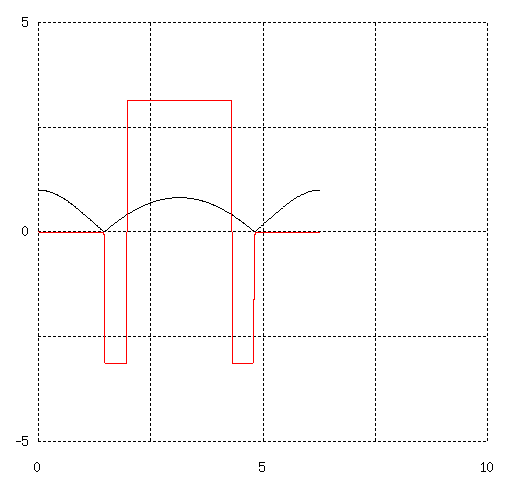
3図 薄肉円筒導体内部の線電流による渦電流の電流分布
黒線が渦電流の大きさ、赤線が渦電流の位相です。
0 <= θ < π と π <= θ < 2*π それぞれの領域で ∫i(θ)*dθ = 0 になり、 円筒の右側を流れる電流が左側から環流していることがわかります。 θ = +-π/2 では電流が流れません。
電流密度が最大になるのは θ=0 の場所ですから、 プログラムでは電流密度を、この最大値で規格化(割る)しています。
また、i(θ) の θ に関する一周積分は 0 になるはずで、 その検証を z3 で行えるようになっています。
平林 浩一, 2016-10