近接導体の渦電流問題 - 導体の渦電流問題 (6)

伝送線路の減衰と伝搬速度に与える渦電流には、 表皮効果と近接効果として知られる伝送に使われる導体自体に生ずるもの以外に、 シールドや隣接導体など、伝送にかかわる導体周辺のありとあらゆる導体に発生します。

1. 線電流による薄肉円筒の渦電流損失

近接導体に生ずる渦電流の理解には、 内側に存在する線電流による薄肉円筒の渦電流を考えるのが良いと思います。

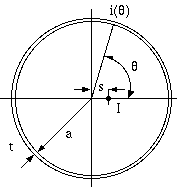
１図 薄肉円筒内部の線電流による渦電流損失

薄肉円筒の中心から s (s < a) 離れた場所に線電流 I が存在する状況を考えると、 下記の結果が得られます。 (注１)

薄肉というのは厚さ方向の電流密度が一定と見做せるという意味で、 電磁波の波長に対して厚さが十分小さいという状況です。 また、線電流というのは電流が流れている導体半径が円筒の半径に比べて 十分小さいという意味です。

                       ∞
  i(θ) = - I/(π*a*t)*Σ((s/a)^n*j*m/(n+j*m)*cos(n*θ))   (1)
                       n=1
                ∞
  Rac/Rdc = I^2*Σ(s/a)^(2*n)*m^2/(m^2+n^2))               (2)
                n=1

  ここに、
	i(θ) = 薄肉円筒の電流密度 (A)
	Rac = 電流 I から見た見掛けの交流抵抗増加量 (Ω)
	a = 円筒の半径 (m)
	t = 円筒の厚さ (m)
	s = 円筒中心から線電流中心までの距離 (m)
	m = 2*π*ω*μ*σ*a*t
	  = ω*μ*Rdc
	Rdc = 薄肉円筒の直流抵抗 (Ω/m)
	ω = 電流の角周波数 (rad/s)
	  = 2*π*f
	f = 電流の周波数 (Hz)
	μ = 透磁率 (H/m)
	σ = 導電率 (S/m)
	σ = 導電率 (S/m)

次に、(2) 式の渦電流損失は線電流 I から見ると、 Rac だけ電気抵抗が増加したように見えます。 この見掛けの電気抵抗は直流で 0、 周波数が大きくなるにつれて当初は周波数の自乗に比例して増加しますが、 その増加の程度は少しづつ減ってゆき、極限値(limit vlue)

  (s/a)^2/(1 - (a/s)^2)                (3)

電気回路として見ると、円筒内の渦電流は電流 I と円筒の相互インダクタンス M によって発生する起電力 j*ω*M*I によって発生するものですが、 周波数が高くなると表皮効果により、 電流が流れる断面積が sqrt(ω) に反比例して減り、 同時に円筒の電気抵抗が sqrt(ω) に比例して増加するため、 円筒の電力損失は周波数に関係なく一定値に収束します。

また、I が円筒中心に存在する場合は渦電流は存在せず、 中心から離れるにしたがって増加し、 増加の程度は (s/a)^2 に比例します。

以上は s < a の場合で、 シールド内部の導体が受けるシールドの影響の近似になりますが、 線電流が円筒の外側に存在する a < s の場合は下記のようになって、 これが高周波に於ける近接導体の影響を近似することになります。

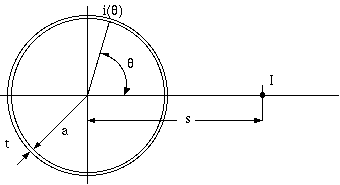
２図 薄肉円筒外部の線電流による渦電流損失

                       ∞
  i(θ) = - I/(π*a*t)*Σ((a/s)^n*j*m/(n+j*m)*cos(n*θ))   (3)
                       n=1
                ∞
  Rac/Rdc = I^2*Σ(a/s)^(2*n)*m^2/(m^2+n^2))         (4)
                n=1

なお、薄肉円筒内部に往復線電流が存在する

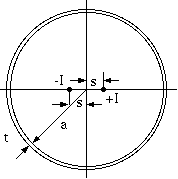
３図 薄肉円筒内部の同一円周上に等間隔の線電流が存在する場合

３図の場合は下記のようなります。

                  ∞
  Rac/Rdc = 4*I^2*Σ(s/a)^(2*n)*(sin(N*π/2))^2/(m^2+n^2))         (5)
                  n=1

また、３相電流だと

                  ∞
  Rac/Rdc = 6*I^2*Σ(s/a)^(2*n)*(sin(N*π/3))^2/(m^2+n^2))         (6)
                  n=1

2. 実験式の工夫

2.1. 密着シールド付き対燃ケーブル

広い周波数範囲で精度の良い近似式を作るのは難しいのですが、 Harold Hughes は下記の実験式を作り、 導体径 0.634 mm、絶縁体径 2,435 mm、シールド厚 0.05 mm の 密着シールド付き対燃ケーブル(close-screened pair)で、 0 - 100 MHz までの周波数による検証を行っています。

  Rac/Rdc = (1 + (3^6 + 8*u^6/(1 - a/(2*s)))^(1/6))/4 + Re       (7)
  Re = 0.8*(sqrt(u) - 0.5) * Rs       (8)
  ここに、
	Rac = シールド付き対燃ケーブルの交流抵抗 (Ω/m)
	Rdc = シールド付き対燃ケーブルの直流抵抗 (Ω/m)
	a = 導体半径 (m)
	s = 導体中心間距離 (m)
	u = a*sqrt(ω*μ*σ)
	ω = 2*π*f (rad/s)
	f = 周波数 (Hz)
	μ = 導体の透磁率 (H/m)
	σ = 導体の導電率 (S/m)
	σ = 導体の導電率 (S/m)
	Re = シールド内渦電流損失による等価抵抗 (Ω/m)
	Rs = シールドの交流抵抗

(8) 式はシールドの交流抵抗の周波数による増加を 若干ゆるやかにした形になっていますが、 近接効果特有の極限値が考慮できず、 周波数が高くなると過大評価になり、Re は無限に大きくなりますから、 利用する場合は極限値を超えていないことを確認すると良いでしょう。

2.2. 隣接導体の渦電流

少し荒っぽいのですが、 H.Hughes は同一円周上に存在する複数の隣接対を 同じ直流抵抗を持つ薄肉円筒で近似する手法を提案しています。 近接効果の渦電流がケーブルの軸方向であることを考えれば、 薄肉円筒を同一円周上の複数の細い導体群の集まりに置き換えても、 導体群のエネルギ損失と円筒のエネルギ損失はほぼ比例するはずで、 悪い方針ではありません。

例えば、中心の 1 対の外側に隣接する 6 対を考えると、 6 対に含まれる 12 本の導体群の直流抵抗に等しい抵抗値を持ち、 6 対の配列円と同じ半径の薄肉円筒を考えると

  b = 3*D .. 6 対の配列円半径は導体の絶縁体径の 3 倍
  t = 3*d^2/b
  ここに、
	d = 導体径 (m)
	D = 対燃コアの絶縁体径 (m)
	b = 等価薄肉円筒の半径 (m)
	t = 等価薄肉円筒の厚さ (m)

N.1. 注１ - 線電流による薄肉円筒の渦電流損失の解析

  H.B.Dwight,- Proximity Effect in Wires and Thin Tubes
	A.I.E.E. Trnas. vol 42, 1923

                ∞
  Rac/Rdc = 1 + Σ((a/s)^(2*n)*(2*m^2/(m^2+n^2))
                n=1

また、F.W.Carter は電力ケーブルのシース(sheaths)に生ずる電力損失を求めるために、 １図、２図のモデルを解析しました。

 F.W.Carter,- Eddy Currents in thin circular cylinders, etc.
	Proc. Cambridge Phil. Soc., 1925-27, 23, p901-906

この後も多くの人々の挑戦が続いて、 例えば、

  V.Belevitch,- Theory of the Proximity Effect in multiwaire cables
	Philips Res. Repts, 32, 16-43, 1977

  V.Belevitch,- Theory of the Proximity Effect in multiwaire cables Part II
	Philips Res. Repts, 32, 96-117, 1977

  G.C.Groenendaal, R.P.Wilson and V.Velevitch,-
	Calculation of the proximity effect in a screened pair and quad
	Philips Res. Repts. 32, 412-428, 1977

N.2. 注２ - 薄肉円筒導体インピーダンスの近似式

H.Hughes は (8) 式の薄肉円筒導体の交流抵抗を次式で求めています。

  Zac = b*v/(8*t)*(sinh(v)+sin(v))/(co0sh(v)-cos(v))-1/4) * π*b^2*σ
	+j*b*v/(8*t)*(sinh(v)-sin(v))/(co0sh(v)-cos(v))) * π*b^2*σ
  ここに、
	Zac = 薄肉円筒導体のインピーダンス (Ω/m)
	    = Rac + j*Xac
	Rac = 薄肉円筒導体の交流抵抗 (Ω/m)
	Xac = 薄肉円筒導体のリアクタンス (Ω/m)
	b = 薄肉円筒導体の内径 (m)
	t = 薄肉円筒導体の厚さ (m)
	v = t*sqrt(2*ω*μ*σ)
	ω = 2*π*f (rad/s)
	f = 周波数 (Hz)
	μ = 導体の透磁率 (H/m)
	σ = 導体の導電率 (S/m)
	σ = 導体の導電率 (S/m)

  S.A.Schelkunoff,- The Electromagnetic Theory of Coaxial Transmission Lines
	and Cylindrical Shields
	BELL SYST. TECH J. 13 Oct. 1934, p532-579

  Rbb = (1/2*b)*sqrt(μ*f/(π*g)*(sinh(u)+sin(u))/(cosh(u)-cos(u))
	+ (a+3*b)/(16*π*g*a*b^2)
  ω*Lbb = (1/(2*b)*sqrt(μ*d/(π*g)*(sinh(u)-sin(u))/(cosh(u)-cos(u))
  ここに、
	Rbb = 同軸ケーブル外部導体の交流抵抗 (Ω/m)
	Lbb = 同軸ケーブル外部導体の内部インダクタンス (H/m)
	a = 同軸ケーブル外部導体の外径 (m)
	b = 同軸ケーブル外部導体の内径 (m)
	u = t*sqrt(2*g*ω*&mul;)
	ω = 2*π*f (rad/s)
	f = 周波数 (Hz)
	μ = 同軸ケーブル外部導体の透磁率 (H/m)
	g = 同軸ケーブル外部導体の導電率 (S/m)
	g = 同軸ケーブル外部導体の導電率 (S/m)

  (a+3*b)/(16*π*g*a*b^2) = 1/4

この Schelkunoff の近似式は円筒導体の表皮効果の解析解に、 変形 Bessel 関数の漸近展開の２次の項までを適用したものですが、 広範囲の周波数領域で良い近似を与えます。