a/s, a/δ の全領域をカバーする近接効果補正係数の近似式を作るのは 非常に難しいのですが、 A.H.M.Arnold は平行円柱導体と平行円筒導体の両方に適用できる下記の近似式を見出しました。 (注1)
P = 1/sqrt(1-A1/(s/(2*a))^2+(A2/(a/(2*a))^4)/(1-A3(/s/(2*a)^2)) (1) ここに、 A1 = f1(sqrt(2)*at/δ)+(1-(at/a)^2-(at/a)(1-(at/a))*f7(sqrt(2)*at/δ))*f4(sqr(2)*at/δ) A2 = f2(sqrt(2)*at/δ)+(1-(at/a)^2)*f5(sqr(2)*at/δ) A3 = f3(sqrt(2)*at/δ)+(1-(at/a)^2)*f6(sqr(2)*at/δ) f7(sqrt(2)*at/δ) = (sqrt(2)at/δ)^3/(400+(sqrt(2)at/δ)^3) at = sqrt(2*a*t - t^2) .. 円柱のとき at = a a = 導体半径 (m) t = 導体厚 (m) s = 導体間隔(導体中心間距離) (m) δ = sqrt(2/(ω*μ*ρ)) .. 侵入の深さ (m) ω = 2*π*f .. 角周波数 (rad/s) f = 周波数 (Hz) μ = 透磁率 (H/m) σ = 導電率 (S/m) σ = 導電率 (S/m)f1(sqrt(2)*at/δ), fd2(sqrt(2)*at/δ), f3(sqrt(2)*at/δ), f4(sqrt(2)*at/δ), f5(sqrt(2)*at/δ), f6(sqrt(2)*at/δ) は小さくはない関数表になっています。
近接効果 - 導体の渦電流問題 (3) (7) 式を計算するのと比べれば遥かに楽ですが、 それでもコンピュータに任せるべき計算量にはなりますから、プログラムを書くべきで、 関数表の部分は プログラム のソースコードか Arnold の論文(注1)を見てください。
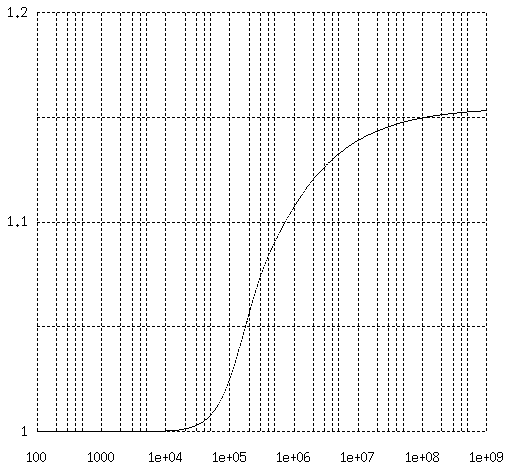
LAN ケーブルの直径 0.5 mm、導体間距離 1.0 mm という条件について P (近接効果補正係数) を 100 Hz から 1 GHz までの周波数について計算した結果は下図のようになります。
近接効果 - 導体の渦電流問題 (3) (2) 式による P の極限値は 1.155 です。

1図 a/s=0.25 軟銅平行線の近接効果補正係数 (A.H.M.Arnold)
Arnold の近似式は実用だけでなく、 Bessel 関数を使う複雑な計算プログラムの検算にも役立ちます。
H.B.Dwight の計算式(注2)、すなわち 近接効果 - 導体の渦電流問題 (3) (7) の プログラミングはかなり面倒です。
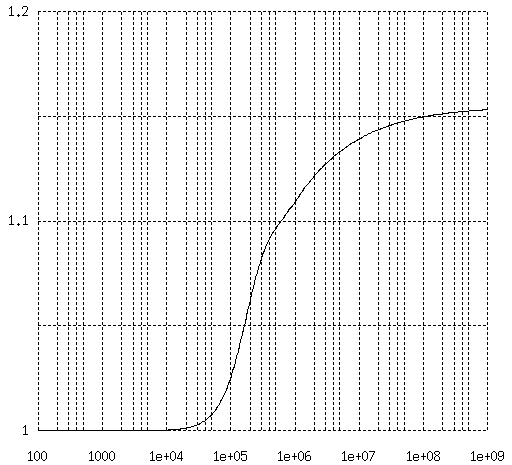
2図 a/s=0.25 軟銅平行線の近接効果補正係数 (H.B.Dwight)
この計算は多量の Bessel 関数の組み合わせを計算するため、 誤差の累積を防ぐのが難しくて、 Bessel 関数の多項式近似を使うと、単独では 1e-6 程度の誤差でも、 P の値になると、 変数が小さい場合の級数展開近似と、 変数が大きいときの漸近展開近似の切替え点で、 4 % 程度の誤差が出ます。
そのため、このプログラムでは、 かなり大きな値まで定義どおりの級数計算を行うようにしてみましたが、 Arnold の近似と若干の違いがでます。 Arnold の結果のほうが自然に見えますが、 古くから使われている DONALD E. AMOS の FORTRAN ライブラリでも同じでした。
級数近似を使う場合は Jns() を Jn() に書き換えてください。 計算が速くなります。 また、切替点より高い周波数では Arnold の結果に近い値が得られます。
A.H.M.Arnold,- Proxmity Effect in Solid and Hollow Round COnductors
Jour. I.E.E. vol 88 Part 2 P349-359, 1941
H.B.Dwight,- Proximity Effect in Wires and Thin Tubes
Tras. A.I.E.E., 1923, p850-859