近接効果 - 導体の渦電流問題 (3)

1. 近接効果の概要

ケーブルの減衰特性と位相歪に最大の影響を与えるのが導体の表皮効果ですが、 同軸ケーブル以外の導体系では、 近接する導体に流れる電流の影響も無視できないことが多く、 この近接導体電流による導体損失の増加を近接効果(proxinity effect) と呼んでいます。

最も典型的な近接効果は往復２導体から構成される平行線(twin lead)や 対撚線(twisted pair)で見られるもので、 歴史的に下記の近接効果補正係数(proximity effect correction factor)で表現されます。 (注１) 

  P = Rac / R0                            (1)
  ここに、
	P = 近接効果補正係数 (proximity effect corrction factor) (1 <= P)
	Rac = 往復円柱導体の交流抵抗 (Ω/m)
	R0 = 単独円柱導体の交流抵抗 (Ω/m) .. 表皮効果のみ
P の値は直流で 1、周波数が高くなるにつれて増加しますが、 表皮効果のように無限に増加するわけではなくて、 後で述べるように、幾何学的配置で決まる極限値に収束します。

定性的には全周波数範囲で、 a を導体半径、s を導体間中心距離、δ を侵入の深さ(skin depth)として、

になります。 導体間距離は導体径、導体径は侵入の深さで規格化されるわけです。

P の値は周波数が低いうちは周波数の自乗に比例して増加しますが、 無限に大きくなるわけではなく、下記の極限値に近付きます。 近接効果は導体外部に存在する電流による電磁誘導起電力による 導体内部のエネルギ損失ですから、 回路的には相互インダクタンス(mutual inductance)に起因するもので、 この起電力は周波数に比例しますが、 起電力が生まれるのは導体表面の侵入の深さの３倍程度の表皮部分だけで、 この表皮部分は周波数の平方根に反比例して薄くなります。 また、表皮部分の抵抗も周波数の平方根に比例して増えるため、 高い周波数では導体外部に存在する電流による発熱は増加しなくなるわけです。

この極限値の存在が近接効果の特徴で、 侵入の深さが円筒導体の厚さ、あるは半径の 1/100 倍以下なら P は周波数の自乗に比例して増加しますが、 1/10 倍程度になると急速に増加がゆるやかになり、 1 倍以下になるとほとんど増加しなくなります。

つまり、高い周波数では近接効果は伝送波形の歪みに関与しなくなります。 

  Phf = 1/sqrt(1 - 1/(s/(2*a)^2))          (2)
  ここに、
	Phf = 高周波の近接効果補正係数 (a/δ > 100)
	δ = sqrt(2/(ω*μ*ρ))  .. 侵入の深さ (m)
	ω = 2*π*f .. 角周波数 (rad/s)
	f = 周波数 (Hz)
	a = 導体半径 (m)
	s = 導体(中心)間距離 (m)
(2) 式が成り立つ条件というのは、軟銅(導電率 5.80e7)の侵入の深さが 
  δ = 6.61e-2/sqrt(f)                 (3)
ですから、LAN ケーブルの導体(a=2.5e-4)で 700 MHz 程度になります。

LAN ケーブルの対の場合はこの程度の周波数になると Phf = 1.155 ですから無視できない損失になりますが、 対間相互インダクタンスを減らすため、 かなり小さなピッチ(length of lay)で撚合わせていますから、 さらに螺旋形状による損失の増加(effect of spiraling)が加わります。

導体間距離が近付くと (2) 式は極めて大きくなって、 s = 2*a で無限大になりますが、この場合は回路的には短絡になって、 伝送路としては使えません。 また、伝送線路では往復導体間の電位差が不可欠ですから、 あまりに導体間距離が小さくなると、 誘電体の絶縁破壊や放電が起きますので物理的限界があります。

なお、(2) 式は厚さが侵入の深さの 3 倍を超えるような円筒導体にも適用可能です。 また、実務書で、よく見掛ける導体間距離が大きいときの高周波近似 

  Phf = 1 + 2*(a/s)^2   (s « a)                   (4)
は (2) 式の平方根を級数展開して高次の項を捨てたもので、 簡単ですが近接導体の影響が (a/s)^2 に比例するという性格を残しています。

(2) 式の条件が成り立たない低い周波数に於ける P の値を求めるのはかなりやっかいな仕事になりますが、 以下、J.R.Carson の方法より用途の広い H.B.Dwight の手法を解説します。

2. 往路が線電流となる円柱導体の渦電流

平行導体の表皮効果の解析に積分方程式を使うという新領域を見出した C. Mannebak は平行線の一方が線電流という状況での、 円柱導体の電流密度を求めました。 (注２)

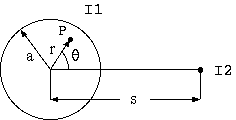
１図 線電流 I1 による円柱導体の渦電流

１図の左側は電流 I1 が流れる半径 a の円柱導体、 その中心から s 離れた場所に電流 I2 の線電流があると、 円柱導体内部の電流密度が (5) 式になることを明らかにしたのです。 

  i(r,θ) = I1/(π*a^2)*j*a*k/2*J0(j*k*r)/J1(j*k*a)
	                    ∞ 
	+ I2/(π*a2)*j*k*a*Σ(an/sn*Jn(j*k*r)/Jn-1(j*k*a)*cos(n*θ))    (5)
	                   n=1
  ここに、
	k = sqrt(j*ω*μ*σ)
	j = sqrt(-1)
	ω = 角周波数 (rad/s)
	   = 2*π*f
	f = 周波数 (Hz)
	μ = 透磁率 (H/m)
	σ = 導電率 (S/m)
	σ = 導電率 (S/m)
	J0(x) = ０階の第１種Bessel関数
	J1(x) = １階の第１種Bessel関数
これは極めて重要な成果で、 線電流に流れる交流電流によって生ずる磁場により円柱内部に渦電流 を生ずるのですが、この渦電流がいかなるものかが実によくわかります。

まず、(5) 式の第１項は既に説明した表皮効果です。 次の第２項が線電流の近接効果になりますが、 周波数 f、導体中心からの距離 r、導体中心と線電流を結ぶ直線との角度(θ) によって電流密度が決まります。

角度(θ)に依存する項は cos(n*θ) だけですから、 同じ半径 r なら

  1. ∫i(r,θ)*tθ の１周積分は 0 (∫02*π(n*θ)dθ = 0)
  2. r = 0 で i(r,θ) = 0
  3. I2 = -I1 なら渦電流は r = a, θ = 0 で最大, I2 = I1 なら θ = π で最大
になることがわかります。 つまり、渦電流は表皮効果で決まる導体独自の電流に重畳される、 円柱導体の軸方向に流れる循環電流なのです。 同じ円周上の -π/2 < θ < π/2 の領域と -π/2 < θ < π/2 の領域が往路と帰路になる循環電流ですから、 よく見掛ける円形の渦ではありません。

(a/s)^n*Jn(j*k*r)/Jn-1(j*k*n) は n の増加につれて小さくなりますので、この無限級数は収束します。

実際に (5) 式第２項を計算してみると、この性格がよく実感できます。

表皮効果や近接効果補正係数を求めるには交流抵抗 Rac を求めなければなりませんが、

の２つの方法があります。

正弦的に変化する量の１周期平均を求める場合は 複素ポインティングベクトル(complex Poynting vector)を使うと便利で、 近接効果補正係数の計算では Carson, Dwight, Butterworth のいずれも、 このやりかたで解いています。 (注３)

導体表面の電界の強さと磁界の強さを求め、 複素ポインティングベクトルを導体表面で一周積分することになりますから、 そう簡単でもないのですが、 １図の状況で、この計算を実効すると、近接効果補正係数は次のようになります。 

  Rac/R0 = 1 + 2*(u0'2+v0'2)/(u0*v0'-u0'*v0)
	 n=∞
	*Σ(a/s)^(2*n)*(un*vn'-un'*vn)/(un-1'^2+vn-1^2))  (6)
	 n=1
R0/Rdc は表皮効果で、後に述べる (8) 式と同じです。

3. 平行往復導体の近接効果

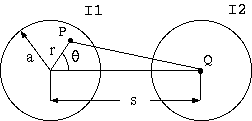
２図 ２本の円柱導体

平行線の場合は２図の I1 = -I2 の条件で (5) 式を両方の円柱断面について積分すれば良いのですが、 この積分は簡単ではありません。

計算の詳細はかなり長くなりますので、 Dwight の論文(注４)を参照していただくことにして、 結果だけ書くことにすると、下記にようになります。 

  Rac/R0 = 1 + 1/(2*abs(A0)^2*(u0*v0'-u0'*v0)
	 n=∞
	*Σabs(Nn)^2*(un*vn'-un'*vn)        (7)
	 n=1

  R0/Rdc = 2/b*abs(A0)^2*(u0*v0'-u0'*v0))   (8)

  j = sqrt(-1)
  j*sqrt(j) = -1/sqrt(2) + j/sqrt(2)
  A0 = b*j*sqrt(j)/(2*J1(b*j*sqrt(j))
  A1 = -a/s  * b*j*sqrt(j)/(2*J0(b*j*sqrt(j))
  A2 = -(a/s)^2  * b*j*sqrt(j)/(2*J1(b*j*sqrt(j))
  ..
  An = -(a/s)^2*a*j*sqrt(j)/Jn-1(b*j*sqrt(j))  (9)

       n=∞
  Bn = -Σ(Ak*(a/s)^(n+k)*(n+k-1)!/(n-1)!/k!*Kk+1(a*k)/Jn-1(b*j*sqrt(j))  (10)
       n=1

       n=∞
  Cn = -Σ(Bk*(a/s)^(n+k)*(n+k-1)!/(n-1)!/k!*Kk+1(a*k)/Jn-1(b*j*sqrt(j))  (11)
       n=1
  ..

  N1 = A1 + B1 + C1 + ..
  N2 = A2 + B2 + C2 + ..
  N3 = A3 + B3 + C3 + ..
  ..
  Nn = An + Bn + Cn + ..  (12)

  u0 + j*v0 = J0(b*j*sqrt(j))
  u0' = (d/db)(u0) .. u0 の b による微分
  un + j*vn = Jn(b*j*sqrt(j))
  un' = (d/db)(un) .. un の b による微分

  b*j*sqrt(j) = j*sqrt(j)*a*sqrt(ω*μ*σ)
  ω = 2*π*f .. 角周波数 (rad/s)
  f = 周波数 (Hz)
  a = 導体半径 (m)
  μ = 透磁率 (H/m) .. 非磁性体なら 4e-7*π
  σ = 導電率 (S/m) .. 軟銅なら 5.80e7
  σ = 導電率 (S/m) .. 軟銅なら 5.80e7
  Jn(x) = n 階の Bessel 関数

かなり複雑な式ですが、計算してみると実感が得られますので、 この後の解説にプログラム例を載せておきます。

なお、上記の B1, D1, .. の符号を反転する、つまり 

  Nn = An - Bn + Cn - Dn + ..
と書き換えると、 平行２線の導体に同方向の電流を流した場合の近接効果補正係数が得られます。

4. 多導体系の近接効果

Dwight は平行２線の解析を導体群に拡張し、 電力送電線に見られるいくつかの導体群の近接効果を計算しました。 (注５)

J.E.L.Tweeddale はこの結果を元に、 電線で多用される７芯導体系の近接効果を求め、 Kenneky の実験結果との一致を確認しました。 (注６)

導体数の増加とともに計算が複雑になりますが、 これらの計算は Dwight が作成した高次の Kelvin 関数表を使って行われました。 ７芯導体系の計算となると、かなりの労力が必要で、 Tweeddale の論文では 88.3 kHz に於ける s/a = 2 と s/a = 3.76 の２点についてのみ計算を実行し、 Kennelly の実験結果との一致を確認しています。

s/a = 2 というのは電線の撚線導体としては最もありふれた構造で、 素線同士が密着した７芯同芯撚線の交流抵抗が同じ面積の単線導体と等しいことは 表皮効果が無限小の電流素線の相互インダクタンスと抵抗の合成回路であるという 回路論的解釈ができる人には当然の結果ですし、 Kennelly も実験的に確認し、定性的な説明もしているのですが、 導体を細かく分割して絶縁すれば表皮効果を低減できると主張する人々はたくさん居て、 詐欺師の嘘に酔う被害者は永遠になくならないのかもしれません。 オーディオ市場特有の世界かもしれませんが。

5. Arnold の近似式と数表

Carson, Butterworth, Dwight らの努力によって平行導体の近接効果補正係数の計算方法はわかったわけでが、 実際の計算は簡単ではありません。

工学的には 根気よく多量の無限級数を数表片手に計算しなくて済む手段がほしいわけですが、 A.H.M.Arnold は 

  φn + j*ψn = Jn+1(x*j*sqrt(j))/Jn-1(x*j*sqrt(j))
を多項式の多項式で近似する手法で、 現時点では最も完成度の高い計算法と数表を作りました。 
  A.H.M.Arnold,- Proxmity Effect in Solid and Hollow Round COnductors
	Jour. I.E.E. vol 88 Part 2 P349-359, 1941

これで計算の努力は劇的に減りましたが、 それでも表を引けば終りというわけではなくて、 ６つの数表を元に、ある程度の計算をする必要があって、 これも次項のプログラミング編で解説します。

6. 近似式の工夫

平行線の表皮効果と近接効果をまとめた実験式として、 Levasseur の発見をもとにした、下記の結果が知られています。 

  Zac/Rdc = (1 + (3^6 + 8*u^6/(1 - a/(2*s)))^(1/6))/4
	+ j*0.455*u^2/(1 + (3^6 + 8*u^6)*(1/6))/sqrt(1 - (a/(2*s))^2)))    (13)
  ここに、
	a = 導体半径 (m)
	s = 導体中心間距離 (m)
	u = a*sqrt(ω*μ*σ)

N. 注

ここで引用する論文はすべて Gauss 単位時代のものですから注意してください。 単位系が変わると数式も変わることを忘れてはなりません。 例えば、相互インダクタンスによる電圧低下なら 

  j*ω*2*I*log(D/B) .. Gauss <-> j*ω*μ/(2*π)log(D/B) .. MKS
といった具合です。 Gauss単位系は真空の誘電率(ε0)と透磁率(μ0)が 1 を基本にしていますから、 当時の式をSI単位系に書き換えるとき、 これらの存在を見失わないように注意しなければなりません。 もちろん、基本単位がCGS(cm, gram, sec)ですから、 MKS(m, kg, sec)への換算も必要です。

なお、Gauss単位系は対応する電気量と磁気量を対等に扱うため、 表現式が対称的になり、 電気量と磁気量とを関連する式に c (光速)が入ってきてますが、 この c は磁気量が電気量の相対論的効果であることの反映です。

最後までGauss単位系で頑張っていた、 J.D.Jackson の Classical Electrodynamics も Third edition でSIに切替え、 E.M.Purcell の Electricity and Magnetism も Third edition でSIに変わりましたが、 学部レベル以上の文献を見るときはGauss単位系の理解が不可欠です。

N.1. 注１ - 平行線の近接効果解析

平行線(parallel wires)の近接効果(proximity effect)の計算を最初に行ったのは 

  J.R.Carson,- Wave Propergation over Parallel Wires: The Proximity Effect
	Phil. Kag., April, 1921, p607-633
です。Carson は (1) 式を R = C*R0 と書いていて、 C は Bessel 関数の商を主役とする、かなり複雑な無限級数になります。

平行２線の伝送線路では電流が相手側導体寄りに偏移しますから、 導体の実効抵抗の増加以外に内部インダクタンスの減少もありますが、 現代のように広帯域のパルス伝送(base band transmission)がなかった時代ですから、 信号の伝搬速度にしか興味がありませんでした。 この時代は挟帯域の変調波による伝送が実用化され始めた時期で、 Carson も変調理論の研究をしています。

なお、同年代にイギリスでも Butterworth が同じ問題に取り組んでいて、 Bessel 関数の組み合わせの無限級数解を得ています。 

  S.Butterworth,- Eddy-Current Losses in Cylindrical Conductors,
    with Special Applications to the Alternating Current Resitance of Shirt Coils
	Philosofical Transactions of the Royal Society, 1921, 222, p.57-100

N.2. 注２ 平行線の積分方程式による解法

  C. Manneback,- An Integral Equation for Skin Effect in Parallel Conductors
	Jour. Math. Phys., April 1922
積分方程式の利点は微分方程式と違って、境界条件が要らないため、 開領域の問題に適していることです。

N.3. 注３ - 複素ポインティングベクトル

正弦的に変化する電場 E と磁場 H のベクトル積 
  S = E X H
をポインティングベクトル(Poynting vector)と呼び、下記の関係があります。 
  -∫sNn*dS = W + dU/dt

  ここに、
	∫s..dS = 閉領域表面の面積分
	Sn = 複素ポインティングベクトルの法線方向成分
	∫v..dv = 閉領域の体積積分
	W = ∫v(i*E)*dv = ∫vσ*E2*dv .. Joule 熱
	U = ∫v1/2*(ε*E2+μH2)*dv .. 電磁エネルギ
	i = 電流密度
	E = 電界の強さ
	ε = 誘電率
	σ = 導電率
	μ = 透磁率
また、共役複素数を使って電場 E と磁場の共役複素数 H* のスカラー積を 複素ポインティングベクトル 
  N = (1/2)*(E·H*)
  ここに、
	N = 複素ポインティングベクトル
	H* = H の共役複素数
を定義すると、下記の関係が得られます。 
  -∫sNn*dS = W + 2*j*ω(Um - Ue)
  ここに、
	Nn = 複素ポインティングベクトルの法線方向成分
	W = Joule 熱の時間平均
	Um = 磁気エネルギの時間平均
	Ue = 電気エネルギの時間平均
こうして、ポインティングベクトルに交流理論を組み合わせることで、 W と全電流から Rac を求めることができます。

内部インダクタンス Li を求める場合は、Ue << Um に注意すれば、 Li = Um/2 が得られます。

N.4. 注４ - 平行２線の近接効果

  H.B.Dwight,- Proximity Effect in Wires and Thin Tubes
	Tras. A.I.E.E., 1923, p850-859
この論文を読むとき、多くの人々が 
  log(D/s) = -(a/s*coa(θ) + (a/s)^2/2*cos(2*θ) + .. (a/s)^n/n*cos(n*θ) + ..)
といった級数展開に首を傾げると思いますが、これは三角形 D,a,s に余弦定理(raw of cosines)を適用して D を消去し、 フーリエ級数(Fourier Series) 
  log(1 - 2*a*cos(x) + a^2) = -2*(a*cos(x) + a^2/2*cos(2*x) + a^3/3(cos(3*x) + ..), -π < x < π, abs(a) < 1
に展開したものです。

これが積分を実効するときの鍵になりますが、 Carson も前記の論文で同じ手法を使っています。

この論文では、 送電線に見られる２導体系と３相３線の三角配置と平行配置などの計算を行っていて、 電力分野への応用を意図していたことがわかります。

なお、この種の論文のコピーを入手するには IEEE Xploreが便利です。

(2), (3), (4) 式の log(d/a), log(b/a), log(D/s) の級数展開については Reference 13, Note 1 を見よとなっていますが、 今は Curtis, H. L.,- An integration method of deriving the alternating-current resistance and inductance of conductors で読めます。

N.5. 注５ - 導体群の近接効果

  H.B.Dwight,- Proximity Effect in group of round wires
	Gen. El. Rev., November 1927, p531-536

N.6. 注６ - ７芯導体系の近接効果

  J.E.L.Tweeddale,- Proximity effect in seven-strand cable
	Trans. Am. I.E.E. 46, 1927, p1148-1152

平林 浩一, 2016-09