近接導体の渦電流問題(プログラミング) - 往復平行線路 (4)

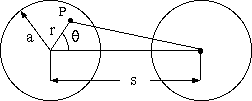
昔のアナログ電話回線から LAN ケーブルなど最近のデジタル伝送路まで、 広範囲で使われる往復平行線路(Two Wires in Return Circuit)は電気・電子技術で重要な役割を果たしますが、 近接効果(proximity effect)と呼ばれる 隣接導体の影響で発生する渦電流(eddy current)の計算 がやっかいで、 ここでは

  H.B.Dwight,- Proximity Effect in Wires and Thin Tubes
	A.I.E.E. Trans., vol 42, 1923, p.850-859

原論文では、最初にMaxwellからKennely、 Carson、Mannebackに至る簡潔な歴史を説明した後、まず、 電流密度の半径方向の変化を考えなくて済む、 薄肉チューブ(thin tube)と線電流(infinitesimal wire)による渦電流問題を解きます。 ここでは log(b/a) のFourier展開が鍵で、 これがこの後の半径方向の積分を可能にするわけですが、この手法は

  H.L.Curtis,- Science Paper No. 374
	Beureau of Srandards, WAshington, D.C., 1920

次いで薄肉円筒による往復平行導体の計算を行い、 単相回路と３相回路のシース(sheath)渦電流を計算した後、 充実円筒での単線往復平行導体の計算を実行、 最後に３角配置と平行配置の単線３相導体の計算を実行しますが、 これらの積分では導体表面の磁界が cos(n*θ) (0<=θ<=2*π)に比例するため、 Poyntingベクタの円周に沿った１周積分は簡単です。

そして最後にBessel関数の要約と簡単な数表があって、 電線に関係する技術者なら、 一度は見ておくべき文献のひとつですが、 この論文の計算手法については、なかなか入手できない 実際に動くプログラムを見ながら原論文を読むと理解しやすいと思います。 疑問が生まれたときは、プログラムを部分的に書き換えて、 個々の数式を計算してみると、意味がよくわかります。

1. 往復平行線路のインピーダンス計算

１図 往復平行線路

H.B.Dwight による計算手順は次ぎのとおりです。 (注２)

  Zac/Rdc = 2/b*A0^2*j*sqrt(j)*J0/J1
                ∞
	+ (1/b)*Σ(abs(Nn)^2*Jn*conj(j*Jn')                           (1)
               n=0
  A0 = b*j*sqrt(j)/(2*J1)
  A1 = -(a/s)*b*j*sqrt(j)/J0
  A2 = -(a/s)^2*b*j*sqrt(j)/J1
  ..
  An = -(a/s)^n*b*j*sqrt(j)/Jn-1                (n != 0)
       ∞
  Bn = Σ(-Ak(a/s)^(n+k)*(n+k-1)!/(n-1)!/k!*Jk+1/Jn-1)
       k=1
       ∞
  Cn = Σ(-Bk(a/s)^(n+k)*(n+k-1)!/(n-1)!/k!*Jk+1/Jn-1)
       k=1
  ..
  N1 = A1 + B1 + C1 + ..
  N2 = A2 + B2 + C2 + ..
  ..
  Nn = An + Bn + Cn + ..

  ここに、
	Zac = 往復平行線路のインピーダンス (Ω)
	Rdc = 往復平行線路の直流抵抗 (Ω)
	  = 1/(π*a^2*σ)
	J0, J1, J2, .. Jn は j*α*a を引数とするBessel関数
	Jn' = (d/dx)Jn(x) .. Jn の微分
	α = sqrt(j*ω*μ*σ)
	j = sqrt(-1)
	ω = 角周波数 (rad)
	  = 2*π*f
	f = 周波数 (Hz)
	μ = 透磁率 (H/m)
	σ = 導電率 (siemens/m)
	a = 導体半径 (m)
	s = 導体中心間距離 (m) (2*a <= s)
	conj(z) = 複素数 z の共役複素数

なお、N1, N2, .. を

  N1 = A1 - B1 + C1 - D1 + ..
  N2 = A2 - B2 + C2 - D2 + ..
  ..
  Nn = An - Bn + Cn - Dn + ..

(1) 式の最初の項が単独円柱導体の表皮効果で、 表皮効果 - 導体の渦電流問題 (1) の (13) 式と同じものです。 次ぎの項が近接効果で、 共役複素数が出てくるのは、 導体表面から導体内部に移動する電場と磁場のエネルギを 複素Poyntingベクトル

  N = EΧH
  ここに、
	N = 複素Poyntingベクトル
	E - 交番電界 (V/m)
	H = 交番磁界 (A-turn/m)
	Χ = ベクトル積

この実部が導体内部でJoul熱として消費されるエネルギ、 虚部が導体内部に蓄積される磁気エネルギで、 内部インダクタンス(internal inductance)の起源となります。

もちろん、Curson や Dwight は実数のPontingベクタで

                2*π 
  W = (a/(4*π))∫Eg*Hθ*dθ
                0
  ここに、
	W = 導体内部で発生するJoul熱
	Eg = 導体の軸方向電界
	Hθ = 導体の円周方向磁界
	θ = 導体中心を極座標原点にしたときの偏角 (rad)
		(相手の導体中心方向が θ=0)

なお、導体内部 P 点の電流密度(current density)は次ぎのようになります。

                     ∞ 
  I/(π*a*a)*A0*J0 + Σ(Nn*Jn*cos(n*θ))
                     n=1
  ここに、
	A0, J0, Nn, Jn は (1) 式の a を 半径 r (0<=r<=a) に置き換えて計算する

1.1. Zac/Rdc の例

例えば、典型的な LAN cable (a=0.25mm, s=1 mm) で 1 kHz から 1 GHz までの Zac/Rdc を計算すると次ぎのようになります。

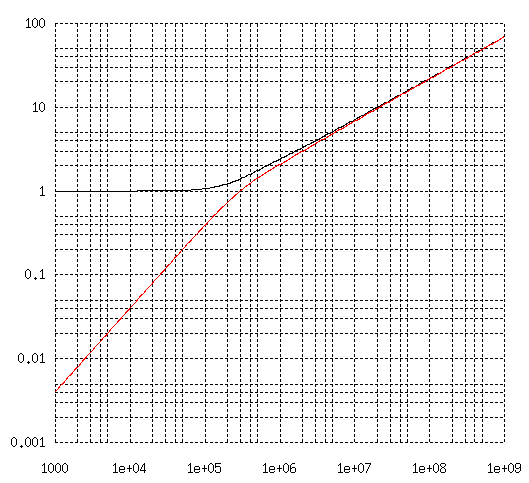
２図 LAN cable の Zac = Rac/Rdc + J*Xac/Rdc

Zac/Rdc の虚部、すなわち、リアクタンスは周波数が小さいうちは周波数に比例、 高周波になると周波数の平方根に比例することに注意してください。 内部インダクタンスは低周波で一定、 高周波になると周波数の平方根に反比例して減少しますが、 これは導体の渦電流すべてに共通した性格です。

1.2. 近接効果係数の計算

Zac/Rdc が得られれば、Zac/Rdc の実部を 単独円筒導体の表皮効果を表す

  Zac_s/Rdc = 2/b*A0^2*j*sqrt(j)*J0/J1

  P = Re(Zac/Rdc) / Re(Zac_s/Rdc)
  ここに、
	P = 近接効果係数
	Re(z) = 複素数 z の実部

  Phf = 1 / sqrt(1 - 1 / (s/(2*a))^2)

1.3. 近接効果係数の例

例えば、前記の LAN cable (a=0.25mm, s=1 mm) で 0.1 kHz から 1 GHz までの P を計算すると次ぎのようになります。 Phf = 1.16 の極限値と比べてみてください。

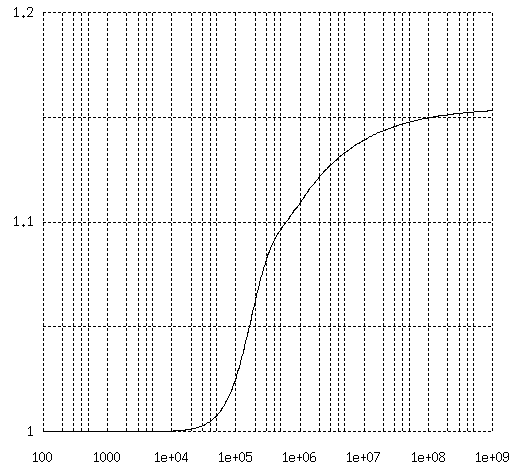
３図 LAN cable の近接効果係数 (縦軸が P、横軸が周波数 Hz)

1.4. 導体内部インダクタンスの計算

Zac の虚部を ω で割れば導体内部インダクタンスが得られます。

  Li = Im(Zac/Rdc) * Rdc
  ここに、
	Li = 導体内部インダクタンス (H/m)
	Im(z) = 複素数 z の虚部

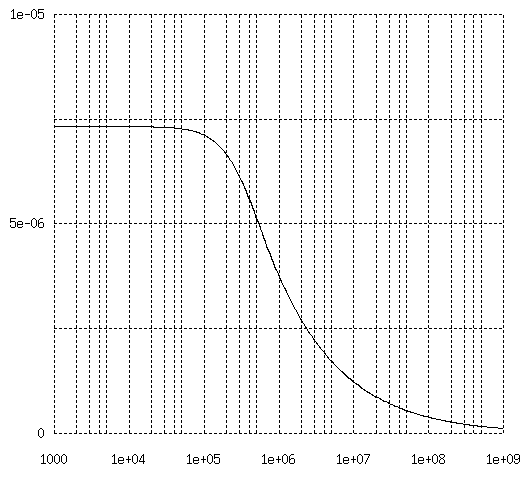
４図 導体内部インダクタンス例

2. プログラム

プログラムはc99以降の複素数をサポートしたc言語で書いてあって、 動作確認は FreeBSD-8.4 (gcc 4.2.1 + gfortran 4.6.3) と FreeBSD-10.3 (clang 3.4.1 + gfortran 4.8.5) で行っています。

複素 Bessel 関数の計算に使われている -lamos (amos.a) は

  http://www.intex.tokyo/unix/cbes/cbes.html

Compile は「make」を実行するだけですが、 プログラムの内容や実行結果の理解には原論文が不可欠で、 この解説は原論文を理解するための障害を少しでも減らすことを目的にしています。

ソースコード

  zac(double f1, double f2) - 往復平行線路のインピーダンス
  proximity(double f1, double f2) - 近接効果係数
  inductance(double f1, double f2) - 往復平行線路の内部インダクタンス
  COMPLEX Idensity(a, s, g, u, f, t) -  １図 P 点の電流密度
        double a - 導体半径 (m)
        double s - 導体間隔 (m)
        double g - 導電率 (S/m)
        double g - 導電率 (S/m)
        double u - 透磁率 (H/m)
        double f - 周波数 (Hz)
        double t - 偏角 (rad)
  f1 は計算する 周波数の下限 f2 は上限です。

近接効果による電流密度は表皮効果に比べて小さいので、 Irt() 関数の

  A0 = 0.5 * b * I * csqrt(I) / Jn(1, A);

を

  A0 = 0;

にして、近接効果による電流単独で見るほうがよくわかります。

3. 注

3.1. 往復平行導体の渦電流(近接効果)解析

最初の往復平行導体の交流抵抗の完全な解析は

  J.R.Carson,- Wave Propergation over Parallel Wires: The Proximity Effect
	Phil. Mag., April, 1921, p.607-633

この別解となる H.B.Dwight の手法は

  Chas. Manneback,- An Integral Equation for Skin Effect in Parallel Conductors
	Journal pf Math. and Physics, April, 1922

3.2. 計算式の注意

原論文では (1) 式が次ぎのようになっています。

  Rac/Rdc = 2/b*A0^2*(u0*v0'-u0'*v0)
                ∞
	+ (1/b)*Σ(abs(Nn)^2*(un*vn'-un'*vn)                       (2.1)
               n=0
  ここに、
	Rac = 往復平行線路の交流抵抗
	un + j*vn = Jn(b*j*sqrt(j))
	un' + j*vn' = (d/db)(Jn(b*j*sqrt(j))
	b = sqrt(4*w/Rdc)

J.R.Carson や Dwight の論文を含めて、この時代はコンピュータが使えませんから、 複素変数 i*sqrt(I)*xのBessel関数は Kelvin関数の数表による実数関数を使う、 かなり手間のかかる仕事になって、 その都度計算するのはたいへんですから、 前もって数表やグラフを作成し、 それを使って概算することになります。

また、当時の伝送波形は狭帯域のアナログ伝送ですから、 線路の高周波抵抗による減衰が興味の対象で、 パルス波形の位相歪に興味がなかったこともあって、 導体の交流抵抗(導体損失)の計算が目標で、 内部リアクタンスは研究の対象外だったのですが、 今はコンピュータが気軽に使える時代ですから、 私が Dwight の結果を拡張して、 交流抵抗だけでなく、導体の内部インダクタンスを含めた 交流インピーダンスを計算するようにしたのが (1) 式です。

なお、当時の単位系はGauss単位系ですから、 変数の単位以外に数式自体も変わってしまうことに注意してください。 例えば、Maxwell-Heaviside方程式なども、まるで違ってきます。 当時の文献の式を使う場合は、 数式自体をSI単位系に書き換えるか、 現在のSI単位の変数をGauss単位に変換して計算し、 得られた結果をSI単位に戻すかすることになりますが、 ここでは前者を使いました。

磁気は電気の相対論的効果だということが知られていなかった時代の Gauss単位系は、 お互いに影響を与えつつも、 それぞれ独立した世界と見られていた電気と磁気を対等に扱い、 真空の誘電率と透磁率を 1 にしていますので、 式中では省略するのが普通で、 SIへの変換作業では見落としがちです。

あと、この論文に出て来る ∠ は階乗(factorial)関数で、 交流理論の偏角ではありません。 例えば、∠n は n! = 1*2*3* .. *n です。 後の Dwight の著作では階乗に ! を使うようになっています。

3.3. Zac の計算法

導体内部で発生するJoul熱の計算に複素Poyintingベクタを使ったのは Carson で、Dwight もそれを踏襲していますが、 往復平行導体の場合は単位長あたりの軸方向電圧と電流から 直接 Zac を求めることもできます。

ただ、複数の導体群から構成される複合導体の場合は、 個々の素線の電流分布がわからないため、拡張性がなく、 複素Poyintingベクタを使う手法が優れています。