ケーブル(electrical cable)の電気特性として重要なのは、 単位長あたりの抵抗(resistance)、キャパシタンス(Capacitance)、 インダクタンス(inductance)、コンダクタンス(conductance)ですが、 ポリエチレンなどの無極性の 優れた絶縁材料を使えば コンダクタンスを無視できることが多く、 キャパシタンスも測定や計算が容易で周波数特性がありません。
しかし、導体の抵抗と導体の内部インダクタンスは 原理的に避けることのできない周波数依存性(frequency dependency)を持ち、 その計算も簡単とは言えず、 ここでは、この導体内部インピーダンス計算の基本を解説します。
導体内部には導体内部を流れる電流自体に起因する交番磁場(alternating magnetic field)と他の導体に流れる電流に起因する交番磁場が発生し、 それがまた渦電流(eddy current)と呼ばれる電流を生成することになりますが、 これら全てを考慮に入れた導体内部の交番電磁場は 下記の3次元の偏微分方程式により高い精度で計算することができます。 (注1)
∇²E = j*ω*σ*μ*E (1) ∇²i = j*ω*σ*μ*i (2) ここに、 E = 電界の強さ (V/m) i = 電流密度 (A/m²) j = sqrt(-1) μ = 導体の透磁率 (H/m) σ = 導体の導電率 (S/m) σ = 導体の導電率 (S/m) ω = 角周波数 (rad/s) = 2*π*f f = 周波数 (Hz)ここでは導体の内部インピーダンスを考えていますから、 電磁場とその工学的解釈である電圧、 電流はすべて正弦波(sine wave)であることを忘れないでください。 インピーダンスは正弦波の電圧電流を前提とした概念です。
交流波形としての正弦波は振幅(amplitude)と位相(phase - タイミング)の二つで記述できますから、 電気工学の交流理論(Alternate Current theory)で発明された 複素表現(phasor)を使うと簡潔に表現できて、 すべての計算は複素演算(complex arithmatic)になります。
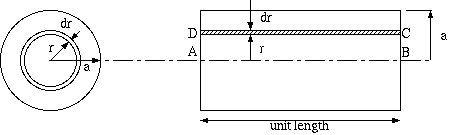
以下、 軸対象になる円形断面の直線導体という簡単で実用的な場合を考えます。

1図 軸対称導体の断面
円形断面の軸対称導体の場合は交流電流の向きが軸方向で、 その電流による磁場が円周方向になり、 電流の大きさは中心軸からの距離だけで決まることになって、 中心軸を原点にした円筒座標を使うと、 1図の半径 r に於ける電流の大きさ i(r) は下記の微分方程式で記述できます。 (注2)
(d/dr)^2(i(r)) + (1/r)(d/dr)(i(r)) = j*ω*μ*σ*i(r) (3) ここに、 r = 半径 (m) i(r) = 導体内半径 r の円周上の電流 (A) (d/dr)(f) = 関数 f の r による1次微分 (d/dr)^2(f) = 関数 f の r による2次微分この方程式はBesselの微分方程式として知られるもので、 Helmholtz方程式(特殊な場合としてLaplace方程式を含む)を 円筒座標で解くときに出てきますが、 その一般解は下記のようになることが知られています。 (注3)
i(r) = C*I0(k*r) + D*K0(k*r) (4) ここに、 k = sqrt(j*ω*μ*σ) j = sqrt(-1) = (1/sqrt(2) + j/sqrt(2))^2 C, D = 定数 (複素数) I0() = 零階の第1種変形ベッセル関数 (modified Bessel function of the first kind of order 0) K0() = 零階の第2種変形ベッセル関数 (modified Bessel function of the second kind of order 0)他の導体の影響を受けない円形断面の渦電流問題は すべてこの式で表現できるわけですが、 以下、ケーブルの問題で最も重要な円筒導体について、 境界条件を考慮した解を求めてみましょう。
円筒内部には電流が存在しない状況での、 2図の外径 a、内径 b の円筒導体について (3) 式を解いてみます。 つまり、単独の円筒導体になりますが、 同軸ケーブルの内部導体として使う場合とか、 他の導電物体から十分に離れた円筒導体の近似になります。
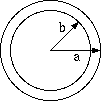
2図 円筒導体
この場合は二つの境界条件
∂i(b)/∂r = 0 (5) i(a) = i0 (6) ここに、 i0 = 導体外表面の電流密度 (観測可能)を (4) に代入して (注4)
0 = C*I1(k*b) + K1(k*b) i0 = C*I0(k*a) + K0(k*a) ここに、 I1(x) = 1階の第1種変形Bessel関数 K1(x) = 1階の第2種変形Bessel関数この2つから
C = K1(k*b)*i0 / (I0(k*a)*K1(k*b) + I1(k*b)*K0(k*a)) * i0 (7) D = I1(k*b)*i0 / (I0(k*a)*K1(k*b) + I1(k*b)*K0(k*a)) * i0 (8)定数 C, D が決まって、 (4) 式から導体内部の電流分布 i(r)/i0 がわかります。
i(r)/i0 = K1(k*b)*i0 / (I0(k*a)*K1(k*b) + I1(k*b)*K0(k*a)) * I0(k*r) + I1(k*b)*i0 / (I0(k*a)*K1(k*b) + I1(k*b)*K0(k*a)) * K0(k*r) (9)導体の内部インピーダンスを求めるには導体内部を流れる 全電流(total current)が必要ですから、 (9) 式を導体断面の全領域で積分すると、
a
I = 2*π*∫i(r)*r*dr
0
= 2*πi0*A/k*(I1(A)*K1(B)-I1(B)*K1(A))/(I0(A)*K1(B)+I1(B)*K0(A)) (10)
ここに、
A = a*k = a*sqrt(ω*μ*ρ) (10a)
B = b*k = b*sqrt(ω*μ*ρ) (10b)
この後、絶えず出てくる sqrt(ω*μ*ρ)
の意味については無限平板の項で説明します。
導体断面方向の電流が存在しない以上 導体断面の電位はどこでも同じで、 導体表面の長さ方向の電位傾度は i0/σ ですから、 単位長あたりの電位差(電圧)を V とすれば
V = i0/σ導体の内部インピーダンスと導体の直流抵抗との比は
Zac/Rdc = (Rac + j*ω*Li)/Rdc = V/I/(π(a*a - b*b))
= (1 - (b/a)^2)
* A/2*((I0(A)*K1(B)+K0(A)*I1(B))/(I1(A)*K1(B)-K1(A)*I1(B)) (11)
ここに、
Rac = 交流抵抗 (Ω/m)
Li = 導体内部インダクタンス (H/m)
ω≈0 と ω=∞ の場合を考えると
I0(A) -> 1 (ω -> 0)
I1(A) -> 0 (ω -> 0)
K0(A)*I1(B) -> 0 (ω -> ∞)
K1(A)*I1(B) -> 0 (ω -> ∞)
Zac/Rdc ≈ (1 - (b/a)^2) (ω -> 0)
≈ (1 - (b/a)^2)*A/2 (ω -> ∞)
b = 0 とすると、この後で述べる円柱導体の場合と同じです。
数値計算の場合は、下記の関係を頭においておくとよいと思います。
I0(0) = 1 I1(0) = 0 K0(∞)*I1(∞) -> 0 I0(∞)/I1(∞) -> 1 K0(∞)/K1(∞) -> 1
同軸ケーブルの内部導体など、 最も一般的な導体は円柱導体(単線)ですが、 この場合は、(11) 式で B = 0 の場合を考えれば、
i(r)/i0 = I0(k*r)/I0(k*a) (12) Zac/Rdc = (A/2)*I0(A)/I1(A) (13)が得られます。 あるいは、(4) 式の一般解で、 K0(0) = ∞ と K0 が導体中心で発散しますから、 D が 0 になることから計算してもかまいません。
簡単ですが、i(r)/i0 を含めて複素数であることを忘れないでください。 電流密度は場所によって大きさが変わるだけでなく、 位相も変わります。 条件によっては表面電流と逆向きに流れるところもあるということです。
よく必要になる低周波と高周波の近似式を求めておくと、
Zac/Rdc ∼ 1 + a^4*(ω*ρ*σ)^2/192
+ j*a^2*ω*ρ*σ/8 * (1 - 1 + a^4/8*(ω*ρ*σ)^2/384)
(a*sqrt(ω*ρ*σ) <= 2 で誤差 0.5 % 以下)
Zac/Rdc ∼ sqrt(2)/4*a*sqrt(ω*ρ*σ) + 1/4
+ 3*sqrt(2)/32/(a*sqrt(ω*ρ*σ)
+ j * (sqrt(2)/4*sqrt(a*sqrt(ω*ρ*σ)/4 - 3*sqrt(2)/32/sqrt(ω*ρ*σ))
(6 <= a*sqrt(ω*ρ*σ) で誤差 0.1 % 以下)
周波数が低いときは Rac は周波数の自乗に比例して増え、
Li は周波数の自乗に比例して減りますが、
周波数が高くなると Rac は周波数の平方根に比例して増え、
Li は周波数の平方根に反比例して減ります。
こういった周波数特性はケーブル伝送独特のもので、
他の電子部品では実現できず、
この性格がケーブルの伝送特性の補償を困難にします。
ここで、直流抵抗が
Rdc = 1 / (π*a^2*σ)であるこを考慮すれば、 表皮効果を決定する要因 a*sqrt(ω*ρ*σ) は
a*sqrt(ω*ρ*σ) = sqrt(2*f*u/Rdc)ですから、非磁性材料の導体であれば、 Zac/Rdc は f/Rdc と導体構造で決まり、 Rdc が小さいほど表皮効果が大きくなることがわかります。 つまり、f/Rdc から Zac/Rdc を求めるための汎用グラフが作れるわけですが、 この関係は円柱導体だけでなく、円筒導体や平板導体、角柱導体などでも成立し、 H.B.Dwightは工学的に有用なグラフをたくさん作成しました。 また、電子回路では高周波で問題になる表皮効果が、 導体サイズが大きい、つまり、 導体抵抗の小さい電力ケーブルでは低い周波数でも表皮効果が問題になる ことが分かります。
なお、 直流に於ける円柱導体の内部インダクタンスは良く知られた μ/(8*π) になることに注意してください。
同軸ケーブルの外部導体は円筒導体になりますが、 円筒外部で電磁場が 0 になりますから、 形状は2図と同じでも、1.1. の解析とは境界条件が逆になります。 つまり、
∂i(a)/∂r = 0 (14) i(b) = i0 (15) ここに、 i0 = 導体内表面の電流密度という境界条件で (3), (4) 式を解かなければなりません。 この条件は円筒中心に円筒に流れる電流と等しい電流が逆向きに流れる場合でしか 実現できないことに注意してください。
この条件で計算をやりなおすと、
C = i0*K1(A)/(I1(A)*K0(B)+I0(B)*K1(A)) (16)
D = i0*I1(A)/(I1(A)*K0(B)+I0(B)*K1(A)) (17)
i1/i0 = (I0(A)*K1(A)+I1(A)*K0(A))/(I1(A)*K0(B)+I0(B)*K1(A) (18)
I/i0 = 2*π*b*b/B*(I0(A)+I1(A)*K0(A)/K1(A))/(I0(B)+I1(A)*K0(B)/K1(A)) (19)
Zac/Rdc = (Rac + j*ω*Li)/Rdc
= ((a/b)^2 - 1)*B/2*(I0(B)*K1(A)+K0(B)*I1(A))/(I1(B)*K1(A)-K1(B)*I1(A)) (20)
ここに、
i1 = 円筒導体内表面の電流密度 (A/m^2)
この結果を 1.1. のケースを比べてみると、
すべての式で a と b が入れ替わっているのに気づきます。
唯一の違いは Zac/Rdc の符号が逆になることですが、
この境界条件を満たすには
円筒中心に円筒の全電流と同じ大きさで逆向きの電流の存在が必要で、
円筒内表面の電圧がその中心電流の向きとは逆になるためです。
同軸ケーブルはHeltzとともにMaxwellの電磁気学の開拓を引継いだ天才 Heavisideの発明ですが、 外部世界とは電磁場がほぼ完全に切り離された独立宇宙が実現できる構造で、 唯一の外部世界との接点が外部導体表面になって、 ここに他の回路が共通インピーダンス(common impedance)で結合すると、 外部回路とのクロストーク(cross-talk 漏話)を発生します。
しかし、 周波数が高くなるにつれて表皮効果によりクロストークの電流は分離します。 同軸ケーブル内部の電流は外部導体内側に集まり、 外部世界のノイズ電流は外部導体の外側に集まるためです。
クロストークは電気回路の大敵ですから、 これは実に優れた構造で、 この表皮効果による一種の遮蔽効果を 伝達インピーダンス(transfer impedance)と呼んでいます。
Zt = Vt/I (21) ここに、 Zt = 伝達インピーダンス (transfer impedance) (Ω) Vt = 同軸ケーブル外部導体外表面の単位長あたり電位差 (V) I = 同軸ケーブルの電流 (A)この値は直流のとき外部導体の直流抵抗に等しく、 周波数が高くなるに従って減ってゆきます。
現実のケーブルの場合は外部導体に編組(braid)構造を採用することが多く、 この場合はどうしても隙間ができますので、 ある程度周波数が高くなると、 隙間を通した外部世界(外部導体表面)とのキャパシタンス結合により Zt は大きくなってゆきます。 この対策としては編組に銅箔やアルミ箔を併用する手法 がよく使われますが、 柔軟性と繰り返し曲げに対する強度が犠牲になります。 外部導体に銅管を使った半硬質(semi-rigid)同軸ケーブルの場合は 極めて完全な遮蔽ができます。
Zt は (16), (17) から次のように計算することができます。
Zt = i(a)/σ/I = (i(b)/I)*(i(a)/i(b)/σ (22)
= (I0(A)*K1(A)+I1(A)*K0(A))/(I1(A)*K0(B)+I0(B)*K1(A)
/ (2*π*b*b/B*(I0(A)*K1(A)+I1(A)*K0(A))/(I0(B)*K1(A)+I1(A)*K0(B)))
細径同軸ケーブルで使われる銅覆鋼線(copper-covered steel) (注5)とか 銅線や銀線に異種金属をメッキ(plating)した導体は 異種金属を同芯円状に接合した バイメタル導体(bimetallic conductor)になります。
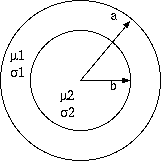
3図 バイメタル導体
この場合は被覆材と芯材それぞれに (4) 式を用意し、
i1(r) = C1*I0(k1*r) + D1*K0(k1*r) (b <= r <= a) i2(r) = C2*I0(k2*r) + D2*K0(k2*r) (0 <= r <= b) ここに、 i1(r) = 被覆材内部の電流密度 i2(r) = 芯覆材内部の電流密度 k1 = b*sqrt(ω*mu;1*σ1) k2 = b*sqrt(ω*mu;2*σ2) mu;1, sigma;1 = 被覆材の mu;, sigma; mu;2, sigma;2 = 芯覆材の mu;, sigma;境界条件
r = 0 で i(r) は有限 (K0, K1 項を含まない) r = b で i(r)/σ が連続 r = b で (1/(μσ)*(d/dr)(i(r)) が連続を考慮して i1(r), i2(r) を求め、
b a
I = 2*π*∫i1(r)*r*dr + 2*π*∫i2(r)*r*dr
0 b
で全電流を求め、
Zac = (i2(a)/σ1)/Iでバイメタル導体の内部インピーダンスが得られます。
この計算は面倒ですが、本質的に円筒導体の計算と同じで、 結果は下記のようになります。
Zac/Rdc = (1 - (b/a)^2)*(1 - σ2/σ1))*A/2*N/D (23) N = I0(A)+I1(B)*K0(A)/K1(B) + sqrt(μ1*σ2/(μ2*σ1)) *I1(C)/I0(C)*((I0(A)*K0(B)-I0(B)*K0(A)/K1(B)) D = I1(A)+I1(B)*K1(A)/K1(B) + sqrt(μ1*σ2/(μ2*σ1)) *I1(C)/I0(C)*((I1(A)*K0(B)-I0(B)*K1(A)/K1(B)) ここに、 A = a*sqrt(j*ω*μ1*σ1) B = b*sqrt(j*ω*μ1*σ1) C = b*sqrt(j*ω*μ2*σ2) a = 導体の外径 (m) b = 導体の芯径 (m) σ1 = 被覆材の導電率 (S/m) σ1 = 被覆材の導電率 (S/m) μ1 = 被覆材の透磁率 (H/m) σ2 = 芯材の導電率 (S/m) σ2 = 芯材の導電率 (S/m) μ2 = 芯材の透磁率 (H/m)なお、
I0(z)*K1(z)+I1(z)*K0(z) = 1/z (24)に注意して、A = B = C の場合を考えれば 円柱導体の結果と一致することを確認できます。
(24) 式の結果は 1943 年に B.R.Tear,Jr と J.R.Webb が求めたもので、 元論文は下記になります。
B.R.Tear,Jr and J.R.Webb,- Skin Effect in Bimetallic Conductors Electrical Engineering, Trans. June 1943, Volune 62, pp 297-302 B.R.Tear,Jr and J.R.Webb,- Copper-Covered Steel Wire at Radio Frequencies Proceedings of the I.R.E, July 1944, pp397-403
円形断面導体の表皮効果に対する良い近似式を作るのは難しいのですが、 Levasseur は円柱導体の表皮効果について、 全周波数領域で +-1% 誤差に収まる面白い近似式を発見しました。 (注6)
次項で解説する無限平板の結果から、 高周波では Rac/Rdc と Xac/Rdc が等しいという結果が得られますので、 Levasseur の結果を内部インピーダンスにも応用できそうですが、 後に Harold Hues が 1 < u で +-7% の誤差で収まる Xac の近似式を作り、 この二つをまとめた結果が次式です。
Zac/Rdc = (1 + (3^6 + 8*u^6)^(1/6))/4
+ j*0.538*u^2/(1 + (3^6 + 8*u^6)^(1/6)) (25)
(25)
ここに、
u = a*sqrt(ω*μ*σ)
a = 導体半径 (m)
ω = 2*π*f (rad/m)
f = 周波数 (Hz)
μ = 透磁率 (H/m) .. 非磁性体なら 4e-7*π
&sigmal; = 導電率 (S/m) .. 軟銅なら 5.8e7
&sigmal; = 導電率 (S/m) .. 軟銅なら 5.8e7
円筒導体については、円筒の内径を基準とした、下記の結果が知られています。
Zac/Rs = sqrt(2)*u/4 - 1/4 + 3*sqrt(2)/(32*u) j*(sqrt(2)*u/4 - 3*sqrt(2)/(32*u)) (6<=u) (26a) ここに、 Rs = 1/(&pi*a^2*&sigma) a = 円筒内径 (m)Rs, a 以外は (25) 式と同じです。
薄肉円筒の場合は、次式が知られています。
Zac/Rdc = u/2*(sinh(u) + sin(u))/(cosh(u) - cos(u)) - t/r +j*(sinh(u) - sin(u))/(cosh(u) - cos(u)) (26b) ここに、 u = t*sqrt(ω*μ*σ) r = 円筒外径 (m) t = 円筒の厚さ (m)現実の導体材料としての円筒は、ほとんど薄肉ですから、 概算には十分な数値が得られます。
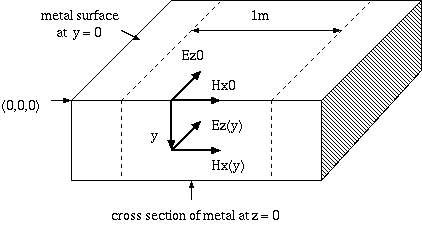
4図 無限平板導体
幅と長さが無限大で厚さが半無限大の平板導体 の内部インピーダンスを考えます。 ちょっと現実離れしていると思われるかもしれませんが、 実際には極めて現実的かつ普遍的で、 しかも高周波に於ける導体の特性を非常によく理解できる条件なのです。
電磁場のサイズ(size 大きさ)は その波長との比較で大小がきまりますから、 高周波の場合は滑らかな曲面である限り、 表皮効果と同じ仕組みで末端に電流が集中する edge effectが問題になるところ以外は 事実上無限平板になります。 同軸ケーブルの内部導体も外部導体も、 その他一見不規則な形状の導体も、 高周波になると、いずれ無限平板と見做せるようになります。
(1) 式の ∇ を直交座標に書き換えると、
(∂/∂x)^2(Ez) + (∂/∂x)^2(Ez) + (∂/∂x)^2(Ez) = j*ω*μ*σ*Ez (27)無限平版の場合は
(∂/∂y)^2(Ez) = j*ω*μ*σ (28)この解は素直な指数関数で表現できて
Ez(y) = Ez0*exp(+-γy) (29)
= Ez0*exp(-y/δ*exp(-j*y/δ) (30)
ここに、
γ = sqrt(j*ω*μ*σ)
= (1 + j)/δ
δ = sqrt(2/(ω*μ*σ))
ω = 角周波数 (rad/s)
= 2*π*f
f = 周波数 (Hz)
μ = 導体の透磁率 (H/m)
σ = 導体の導電率 (S/m)
σ = 導体の導電率 (S/m)
δ は表皮深さ(skin depth) と呼ばれる重要な指標で、
(28) 式は表面から δ 深くなる度に電磁場が 1 neper 減衰し、
1 radian 位相が遅れることを意味します。
(注7)
この減衰はかなり大きなもので、表面から表皮深さ(skin depth)の3倍までの部分にほぼ全電流が集中しますから、 高周波では導体表面の極めて僅かな厚さしか利用できないことになります。
δ の値を求めるには導電率 μ と透磁率 σ の具体的な値が必要ですが、 注8に一般的な金属の値をまとめてあります。
ケーブルの導体として一般的な軟銅(soft annealed copper)だと
δ = 6.61e-2/sqrt(f) ここに、 δ = 表皮深さ (skin depth) (m) f = 周波数 (Hz)ですから、10kHz で 0.66 mm、100 kHz で 0.21 mm、1 MHz で 66 um、 100 MHz で 6.6um、1GHz で 2.1um といった大きさですから、 1 MHz でも表面の 0.2 mm 程度にしか電流が存在しないことになります。
このように高周波電流が導体表面の極めて薄い層に集中する現象は 表皮効果(skin effect)と呼ばれ、 導体形状に関係なく内部インピーダンスのほとんどを決定します。
幅 1 m あたりの全電流は
∞
Iz = ∫σ*Ez(y)*dy = σ*Ez0*δ/(1+j)
0
従って、インピーダンスは
Zac = R + j*X = (1 + j)/(σ * δ) (31)
= Rs * (1 + j) (32)
ここに、
Rs = 1 / (σ*δ) (Ω) (33)
Rs は表面抵抗(surface registance)と呼ばれ、
導体の厚さが表皮深さの 3 倍を超える条件で
高周波抵抗を求めるとき、極めて有効な概念です。
(注9)
例えば、高周波の同軸ケーブルなら、
内部導体表面と外部導体内表面の表面抵抗を使って
Rac = Rs/(2*π*b)*(1 + b/a) ここに、 Rac = 高周波の同軸ケーブルの交流抵抗 (Ω/m) a = 内部導体半径 (m) b = 外部導体半径 (m)中心間距離が大きく近接効果が無視できるような平行往復導体なら、 往復2導体の表面抵抗を使って
Rac = 2*Rs/(2*π*a) ここに、 Rac = 平行往復導体の交流抵抗 (Ω/m) a = 導体半径 (m)といった計算ができます。
なお、(3) 式で純抵抗とリアクタンスが等しいことに注意してください。
Zac = R + j*ω*Lという抵抗とインダクタンスの直列回路モデルとして解釈すると、
R = ω*Lつまり、 電流が抵抗に流れる電流とインダクタに流れる電流が等しくなるように分布する ということで、 高周波であればあらゆる状況で成立します。
この性質から下記の考察により高周波ケーブルの位相歪が減衰と等しいという 重要な結果が得られます。
高周波ケーブルの基本的関係
Z0 = sqrt(L/C) α = Rac/(2*Z0) β = ω*sqrt(L*C) ここに、 α = 減衰定数 (neper/m) β = 位相定数 (rad/m) Rac = ケーブル導体の交流抵抗 (&Ohm;/m) Z0 = ケーブルの特性インピーダンス (Ω) C = ケーブルのキャパシタンス (F/m) L = ケーブルのインダクタンス (H/m)で L を外部インダクランスと内部インダクタンスに分解し
L = Le + Li ここに、 Le = ケーブルの外部インダクタンス (H/m) Li = ケーブルの内部インダクタンス (H/m)β を外部インダクタンスと内部インダクタンスに依存する部分に分けると
β = ω*sqrt(L*C) = ω*sqrt(Le*C*(1 + Li/Le))高周波では表皮効果により Li << Le になることに注意して
β ≈ ω*sqrt(Le*C * (1 + Li/(2*Le))
≈ ω*sqrt(Le*C) + (ω*Li/2)*sqrt(C/Le)
= ω*sqrt(Le*C) + (ω*Li)/(2*Z0)
= ω*sqrt(Le*C) + Rac/(2*Z0)
= ω*sqrt(Le*C) + α (34)
(32) 式の第1項が信号の位相遅れ、すなわち遅延を生む原因で、
位相定数の圧倒的部分を占め、
オシロスコープやネットワークアナライザなど
多くの測定機で容易に測定できます。
一方、第2項は周波数軸測定のネットワークアナライザによる測定は無理ですが、 時間軸測定のオシロスコープでパルス波形の立上りの歪として容易に観察できます。 第1項に比べて極めて僅かな第2項がオシロスコープで容易に認識できるのは、 第1項が信号波形の遅延として機能するため、 オシロスコープではタイミングの違いとして認識され、 波形自体が変わらないのに、 第2項は波形そのものを変えてしまうためです。
つまり、この減衰と同じ大きさの第2項が位相歪を与え、 パルス波形伝送で重要な役割を果たすことになります。 このメカニズムはまた「減衰が歪を生む」とか「減衰を減らすと歪が減る」 といった誤解を生む原因ともなります。
以上の解析結果を見ると、 Zac/Rdc が
Zac = Σf(Ai * sqrt(ω * μ * σ))
i
ここに
Ai = 空間の幾何学的構造と電気的特性で決まる定数
になっていることに気づきます。
これは渦電流が表皮深さと空間構造で決まるためですが、
直流抵抗 Rdc は 1/σ に比例しますから、
非磁性体で構成される通常の伝送路では、
Zac/Rdc = F(f/Rdc) ここに f = 周波数 (Hz) Rdc = 直流抵抗 (&Ohm;/m)の関係があって、 幾何学的電磁的に相似なら Zac/Rdc が変わらないことがわかります。 つまり、同一構造な上記の関係を数表かグラフにしておけば、 いちいち面倒な計算をしなくて済みます。 (注10)
Dwight は多くの構造について、このグラフを作成しましたが、 現代の数値計算でも、 解析対象を誤差の少ないサイズに変換するために利用することができます。 例えば、寸法を k 倍した場合は、 周波数を 1/k^2 倍すれば同じ結果が得られるわけです。
(1), (2) 式はHeaviside表現によるMaxwell方程式
(3) 式を求める方法はいくつかありますが、
軸対称円筒座標の場合はLaplace演算子が
この他、古くから知られている電磁気学の初歩的方法としては、
電流と磁場の関係を与えるAmpereの法則と
電磁誘導のFaradayの法則を使うもので、
1図の半径 r の円筒内を流れる電流と半径 r の磁場の強さの関係
もっと一般的に扱う場合はベクトルポテンシャル(vector potential)
を使うのが普通で、最近は、こちらが普通になっています。
例えば、
Maxwell方程式を時間のみに依存する部分と場所のみに依存する部分に
変数分離するHelmholtz方程式から出発すると、
さらにすっきりします。
Bessel関数は理工学の広範な分野で重要な役割を果たしますので、
文献も非常に多いのですが、私が楽しく読めたものをあげておきます。
Bessel関数の微積分には、
多くの公式が知られていますが、
ここでは下記の関係が使われています。
これらの関係は無限個の多項式で定義されるBessel関数の定義から
一眼でわかります。
Bessel関数にはいろいろな変種があって、
本来のBessel関数 J(), Y() が使われることも多いのですが、
今はコンピュータで簡単に計算できますので、
ここでは簡潔な数式表現ができる変形 Bessel関数を使いました。
コンピュータが実用化されるまでは、数表で関数値を求めながら、
長い時間と多量の紙を消費しながらの計算ですから、
複素数のBessel関数計算ではKelvin関数と呼ばれる
今では昔の人々の苦労をコンピュータが引き受けてくれますので、
何の苦労もなく、瞬時に計算を済ませることができますが、
プログラミングの技術が不可欠ですから、
これについては後述します。
銅覆鋼線(copper-covered steel)は小径同軸ケーブルの抗張力(機械的強度)
を高めるために使われます。
B.R.Tear,Jr and J.R.Webb の論文で検証に使われた導体は
Copperweld Steel Company製の 40 % 導電率 10 AWG で、
その物性は次のとおりです。
4.1. 注1 - 導体内の交流電磁場の偏微分方程式
rotH = i + ∂D/∂t
rotE = -∂B/∂t
divD = ρ, divB = 0, i = σE
に於いて、導体中で ∂D/∂t << i が成り立つことを利用して、
∂D/∂t を無視し、
交流理論による微分演算子変換
∂/∂t → j*ω
を行った結果です。
4.2. 注2 - 円形断面導体の交流電流偏微分方程式
∇²(V) = (1/r)*(∂/∂r)(r*(∂V/∂r))
になりますから、(2) 式の ∇² を軸対称円筒座標に書き換えるだけで
(3) が得られます。
r
2*π*r*H = ∫i*2*πr*dr
0
を r で微分して
∂i/∂r + H/r = i (n.1.1)
次に1図の中心軸に流れる電流を i0 として、
中心軸と半径 r の円筒を通る閉回路 A->B->C->D->A の誘導起電力の関係
r
(i0 - i)/σ = -∂/∂t∫μH*dr (n.1.2)
0
を r で微分して
∂i/∂r = μσ*∂H/∂t
あとは (x.1.2) に r を掛けて r で微分し、(x.1.1) を使うと (3) 式が得られます。
この発想だと、内側の円筒状部分ほど錯交磁束が増えますから電流が流れにくくなって、
外側を流れるはずという理解で、表皮効果に馴染むことができます。
∇²A = -μ*J
J = σ*E = -σ*∂A/∂t
ここに、
A = ベクトルポテンシャル (weber/m)
J = 電流密度 (A/m^2)
から、
ベクトルポテンシャルAの方向がが電流の方向と一致していることに注意して、
1次元なら
∇²Ax = μσdAx/dt
交流なら
A = j*ω*μ*σ*A0*exp(j*ω*t)
として、
∇²Ax = (1/r)((d/dr)(r*dAx/dr)
円筒座標に変換すれば
(d/dr)^2(Ar) + (1/r)*(d/dr)(Ar) = j*ω*μ*σAr
このBessel方程式の解は r = 0 に於ける A の値を A(0) として、
A(r) = A(0)*I0(sqrt(j*ω*μ*σ)*r)
になります。
4.3. 注3 - Bessel関数の参考書
N.W.McLachlan,- Bessel Functions for engineers
(Oxford Engineering Science Series), 1955
Frank Bowman,- Introduction to Bessel Function
(Dover Publications Inc.), 1958 ISBN 0-486-60462-4
Dover には良い本が多いのですが、これは和訳もあります。
フランク・ボウマン,- ベッセル関数入門
(日新出版) ISBN4--8173-0033-7
円筒導体の表皮効果は典型的な応用の一つなので、
このいずれでも触れていますが、
当時は Gauss 単位系(CGS)だったため、
式自体も現在の SI(MKS) 単位系とは違っていて、
係数や単位の違いに注意して読んでください。数式自体も違ってきます。
電気工学の渦電流問題に関する論文は極めて多いのですが、
解析的手法による優れた論文が書かれた時代はGauss(CGS)単位系ですから、
この単位系の違いに注意して読む必要があります。
例えば、Gauss単位系では真空の誘電率と透磁率が 1 ですから、
数式では省略されるのが普通で、
SI(MKS)単位系に書き換えるとき、
見落としがちです。
4.4. 注4 - Bessel関数の微積分
(d/dx)(I0(x) = I1(x)
(d/dx)(K0(x) = -K1(x)
(d/dx)(x*I1(x)) = x*I0(x)
(d/dx)(x*K1(x)) = -x*K0(x)
∫x*I0(k*x)*dx = (x/k)*I1(k*x)
∫x*K0(k*x)*dx = -(x/k)*K1(k*x)
bern(x) + j*bein(x) = Jn(x*j*sqrt(j)) = In(x*sqrt(j))
kern(x) + j*kein(x) = jn*Kn(x*sqrt(j))
ここに、
j = sqrt(-1)
Jn(x) = n 階の第1種 Bessel 関数
In(x) = n 階の第1種変形 Bessel 関数
Kn(x) = n 階の第2種変形 Bessel 関数
で定義される実数関数 ber, bei, ker, kei が唯一の計算手段でした。
4.5. 注5 - 銅覆鋼線
a = 0.1303e-3 (m)
b = 0.1024e-3 (m)
σ1 = 3.583e5 (S/m)
σ1 = 3.583e5 (S/m)
σ2 = 5.464e7 (S/m)
σ2 = 5.464e7 (S/m)
μ1 = 1.0*4*πe-7 (H/m)
μ2 = 7.88*4*πe-7 (H/m)
Rac/Rdc = (1 + (3^6 + 8*u^6)^(1/6))/4
という全周波数領域で +-1% 誤差で収まる近似式を見つけたという
短い論文です。
Levasseur A.,- Calcul rapide de l'effect Kelvin par une nouvelle formule
valable en toutes circumstances
(Revne generale de l'Electricite, dec 1929)
| Metal | Conductibity (S/m) | Temperature Coefficient |
|---|---|---|
| Metal | Conductibity (S/m) | Temperature Coefficient |
| Alminium | 3.54e7 | 0.0039 |
| Brass (somewha variable) | 1.4e7 | 0.002 |
| Copper (annealed) | 5.80e7 | 0.00393 |
| Copper (hard drawn) | 5.65e7 | 0.00382 |
| Constantan | 2.04e6 | 0.000008 |
| Gold (pure) | 4.10e7 | 0.0034 |
| Iron (pure) | 1.00e7 | 0.0050 |
| Lead | 4.54e6 | 0.0039 |
| Mercury | 1.04e6 | 0.00089 |
| Nickel | 1.28e7 | 0.0006 |
| Silver | 6.15e7 | 0.0038 |
| Tin | 8.67e6 | 0.0042 |
| Zinc | 1.76e7 | 0.0037 |
導電率の温度係数はすべて負で、温度が高くなると導電率は下がります。
透磁率は非磁性体なら 4e-7*π (H/m) ですが、 鉄とニッケルのような磁性体は組成や加工方法で大きく変わり、 実際に使用する素材と条件で実測するしかありません。
無限平板の場合は幅と深さ(断面積)が限大ですから、直流抵抗が 0 になって、 Zac/Rdc が使えず、観測可能なのは表面の電位差だけですが、 理論的に全電流がわかりますから、 表面の電位傾度と全電流の比としてのインピーダンスが定義できて、 それが表面インピーダンスになります。
幾何学的電磁的相似な非磁性体の伝送路で Zac/Rdc が sqrt(f/Rdc) で決まってしまうという性格は、 Maneback の積分方程式から一般的に成立することがわかりますので、 あらゆる構造の伝送路で使えます。
導体材料が磁性体の場合は、 例えば、円柱なら半径 a、円筒なら導体の等価半径
at = sqrt(2*a*t - t^2/)/δ ここに a = 円筒外径 (m) t = 円筒の厚さ (m) δ = 表皮深さ (m) at = 等価半径 (m)などの導体の構造を決定するパラメータを使って、 a/δ とか at/δ を使うとスケーリング可能になります。
平林 浩一, 2016-09,2017-08-09