TDR(Time Domain Reflectmetry)は伝送線路の時間領域での電磁波の反射波、 TDT(Time Domain Transmission)は伝送線路の時間領域での電磁波の透過波 (こちらは受端の反射波も加わったもの)を観測する手法ですが、 前者はVNA(Vector Netwark Analyzer)のS11 後者はS21をFourier 変換で時間領域に変換したもので、 物理的には同じ内容です。 ただ、観測者にとっても測定原理としても、 広帯域のパルス波形を考える場合はTDR/TDT、 狭帯域の場合はVNAに利点があります。
TDR/TDTのシミュレーション技法としては SPICEのように時間領域で数値積分を行う方法と、 時間軸テータとしての入力波形をFourier変換で周波数領域に変換して、 伝送システムのシステム関数(周波数特性)を乗算したうえで、 Fourier逆変換して時間軸波形に戻す方法があって、 ケーブルのようにインダクタンスと導体抵抗の周波数特性を無視できない場合は、 周波数領域で解析するほうが精度の高い結果が得られますし、 L(インダクタンス)、C(キャパシタンス)、R(抵抗)、G(コンダクタンス)といった 回路理論の世界を越えた解析ができますので、 ここでは後者の方法を説明します。 (注1)

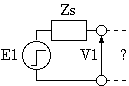
1図 TDR
TDRの目的は未知回路のステップ応答(Step Response を求めることですが、 測定システムとしては立上りが速く周期の長い方形波と 広帯域のオシロスコープの組み合わせを使うのがふつうです。 周期が短いとステップ応答でなく方形波応答になってしまいます。
オシロスコープで観測するのは1図の V1 ですが、 この電圧は電源 E1 から入射した電磁波と未知回路のどこかから反射してきた電磁波の和になります。 反射波が観測されない場合は、 未知回路の入力インピーダンスが Zs に等しい場合、 反射波が1つしか観測されない場合は未知回路の中で入射電磁波が完全に吸収される、 例えば、伝送線路が無限に長いか、 伝送線路の特性インピーダンスに等しい負荷で終端されているか、 伝送線路の損失が極めて大きくて反射波があっても減衰してしまうといった場合です。
未知回路の周波数特性を時間軸特性から理論的に把握する場合は、 インパルス応答を使うのが素直ですが、 測定システムとしては幅の狭いパルスを発生する回路の実現は極端に難しいので、 ステップ応答を使うことになって、 立上り時間 9 ps といったものも市販されています。
測定機としてのTDRは電圧 V1 を入射波に対する比で表示したり、 未知回路のインピーダンスで表示したりするのが普通ですが、 後者が正しいインピーダンスと一致するのは最初の反射波だけですから、 注意が必要です。例えば、 TDR によるケーブル測定の謎 を見てください。
TDRのシミュレーションを周波数領域で行う場合の手順は 下記のようになります。
g(t) が V1(t) になります。
コンピュータの場合、フーリエ変換は離散フーリエ変換になりますが、 計算量が多く時間がかかりますので、 Fast Fourie Transform(高速フーリエ変換)と呼ばれるアルゴリズムを使います。 馴染みのないかたは私の解説でよければ フーリエ変換と線形システムの基礎を見てください。
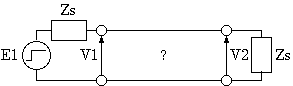
2図 TDT
TDTはTDRに接続した試料終端側の波形を観測しますが、 この場合は試料終端に入射した波形、 つまり、試料始端の透過波形が試料中で減衰したり歪んだ電磁波と、 その電磁波が試料終端の Zs で反射した反射波の合計を観測することになります。
このシミュレーション手順は下記のようになります。
3C-2V程度の同軸ケーブルをTDRで観測する場合を想定しています。
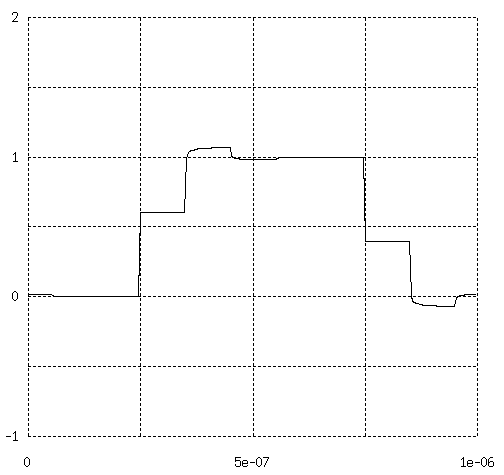
3図 下記 script の実行結果
この script で使われているfftコマンドは フーリエ変換と線形システムの基礎に添付してあります。
実際にシミュレーションを行う場合は、 上記解説にあるように、 グラフ作成を行うプログラムにパイプラインで接続してグラフ化するのが Unix的な使いかたになります。
このプログラムをそのまま動かすとTDRのシミュレーションになりますが、
.. TDR() # TDT() ..を
# TDR() TDT()と書き換えればTDTのシミュレーションになります。
この直前にある RC() は R-C 直列回路のTDR、 RL() は R-L 直列回路のTDRシミュレーションになります。
scriot を少し書き換えると、 いろいろな状況をシミュレートできますので、 実験してみてください。
なお、この例では見やすいように方形波応答になっていますが、 実際のTDR/TDTに近付けるには、 方形波の周期を長くして、FFT のデータ数も増やし、 最後の表示部分で立上りに近い部分だけを表示するようにします。
#! /bin/sh
# TDR, TDT simoulation
_Z0=75 # 試料の特性インピーダンス (Ohm)
_a=1.373e-6 # 減衰定数 = _a * sqrt(f) + _b * f (neper/m)
_b=8.385e-12
_eps=2.3 # 誘電体の比誘電率
_r=1e-3 # 試料の導体抵抗 (Ohm)
_len=50 # 試料長 (m)
_Nr=256 # FFT のデータ数 (2^N)
_Fr=1e6 # 方形波の周波数 (Hz)
_Tr=1e-9 # 方形波の立上り時間 (s)
/usr/bin/awk '
BEGIN {
N = '$_Nr'
Fr = '$_Fr'
Tr = '$_Tr'
PI = atan2(0, -1)
square_wave(N, Tr, Fr)
for (i = 0; i < N; i++) {
t = i / N / Fr
print t, x[i], y[i]
}
exit 0
}
# tr = 10% - 90% rise time
function square_wave(n, tr, f, i, n1, n2, n3, n4, n5, n6, dn) {
dn = int(0.8 * tr * f * n / 2)
if (dn % 2)
dn++; # to pass 0 (fft needs this)
if (dn > n / 4)
dn = n / 4
n1 = n / 4;
n2 = (3 * n) / 4
n3 = n1 - dn
n4 = n1 + dn
n5 = n2 - dn
n6 = n2 + dn
for (i = 0; i < n3; i++) {
x[i] = -1.0
y[i] = 0.0
}
for ( ; i < n4; i++) {
x[i] = (i - n3)/dn - 1
y[i] = 0.0
}
for ( ; i < n5; i++) {
x[i] = 1.0
y[i] = 0.0
}
for ( ; i < n6; i++) {
x[i] = 1 - (i - n5)/dn
y[i] = 0.0
}
for ( ; i < n; i++) {
x[i] = -1.0
y[i] = 0.0
}
}
' | fft | /usr/bin/awk '
BEGIN {
_Z0 = '$_Z0'
_a = '$_a'
_b = '$_b'
_v = 1 / sqrt('$_eps')
_r = '$_r'
len = '$_len'
Fr = '$_Fr'
PI= atan2(0, -1)
K = 0
}
{
F[K] = $1
X[K] = $2
Y[K++] = $3
}
END {
# normalize(K)
# RC()
# RL()
TDR()
# TDT()
for (i = 0; i < K; i++)
print F[i], X[i], Y[i]
}
function normalize(n, i) {
for (i = 0; i < n; i++) {
X[i] /= n
Y[i] /= -n
}
}
function TDT( a, b, w) {
for (i = 0; i < K; i++) {
if (i == 0) { # DC
x = 50 / (50 + 50 + _r * len)
y = 0
}
else {
w = 2 * PI * F[i]
a = _a * sqrt(F[i]) + _b * F[i]
b = w / 2.99792458e8 * sqrt(2.3) + a
V2(50, 0, 50, 0, _Z0, a, b, len)
}
Mul(x, y, 2, 0)
Mul(X[i], Y[i], x, y)
X[i] = x; Y[i] = y
}
}
function TDR( i, a, b, w) {
len = 10
for (i = 0; i < K; i++) {
w = 2 * PI * F[i]
a = _a * sqrt(F[i]) + _b * F[i]
b = w / 2.99792458e8 * sqrt(2.3) + a
if (i == 0) { # DC
x = 1e-6; y = 0
}
else
Zoc(_Z0, a, b, len)
Div(x, y, x + 50, y)
Mul(X[i], Y[i], x, y)
X[i] = x; Y[i] = y
}
}
function RC( i, R, C, w) {
R = 1e3; C = 1e-10
for (i = 0; i < K; i++) {
w = 2 * PI * F[i]
Div(1, 0, 1, w*C*R)
Mul(X[i], Y[i], x, y)
X[i] = x; Y[i] = y
}
}
function RL( i, R, L, w) {
R = 1e3; L = 1e-3
for (i = 0; i < K; i++) {
w = 2 * PI * F[i]
Div(0, w*L, R, w*L)
Mul(X[i], Y[i], x, y)
X[i] = x; Y[i] = y
}
}
# Zoc = Z0 * coth((α + j * β) * l)
function Zoc(z0, x1, y1, l) {
Tanh(x1 * l, y1 * l)
Div(1, 0, x, y)
x *= z0
y *= z0
}
# Zin = (Zt/Z0 + tanh(γ*l) / (1 + (Zt/Z0)*tanh(γ*l)) * Z0
function Zin(z0, x1, y1, l, x2, y2, x3, y3, x4, y4) {
Tanh(x1 * l, y1 * l)
x3 = x
y3 = y
Mul(x, y, x2 / z0, y2 / z0)
x4 = x + 1
y4 = y
Add(x3, y3, x2 / z0, y2 / z0)
Div(x, y, x4, y4)
x *= z0
y *= z0
}
# V2 = ケーブル受端電圧
# V2 = 1/2 * 1/(cosh(γ*l) + z0/(Zs+Zt)*(1+(Zs*Zt/z0^2))*sinh(γ*l))
# Zs = xs + j*ys, Zt = xt + j*yt
function V2(xs, ys, xt, yt, z0, x1, y1, l, a, x2, y2, x3, y3) {
Cosh(x1 * l, y1 * l)
x2 = x; y2 = y
Sinh(x1 * l, y1 * l)
x3 = x; y3 = y
coef(_Z0, 50, 0, 50, 0)
Mul(x, y, x3, y3)
Add(x, y, x2, y2)
Div(1, 0, x, y)
Mul(x, y, 50, 0)
Div(x, y, 50 + 50, 0)
}
function coef(z0, xs, ys, xt, yt, z2) {
z2 = z0 * z0
Mul(xs, ys, xt, yt)
x /= z2; y /= z2
x += 1
Div(z0 * x, z0 * y, xs + xt, ys + yt)
}
function atanh(x) {
return 0.5 * log((1 + x) / (1 - x))
}
# 復素数演算
function Tanh(x1, y1, e, f, d) {
e = exp(2 * x1)
f = 1 / e
d = 0.5 * (e + f) + cos(2 * y1)
if (d == 0) {
e = exp(x1)
f = 1 / e
x = 0
y = (e + f) * sin(y1)
}
else {
x = 0.5 * (e - f) / d
y = sin(2 * y1) / d
}
}
function Add(x1, y1, x2, y2) {
x = x1 + x2
y = y1 + y2
}
function Mul(x1, y1, x2, y2) {
x = x1 * x2 - y1 * y2
y = x1 * y2 + y1 * x2
}
function Div(x1, y1, x2, y2, r2) {
r2 = x2 * x2 + y2 * y2
x = (x1 * x2 + y1 * y2) / r2
y = (y1 * x2 - x1 * y2) / r2
}
function Sinh(x1, y1, e, f) {
e = exp(x1)
f = 1 / e
x = 0.5 * (e - f) * cos(y1)
y = 0.5 * (e + f) * sin(y1)
}
function Cosh(x1, y1, e, f) {
e = exp(x1)
f = 1 / e
x = 0.5 * (e + f) * cos(y1)
y = 0.5 * (e - f) * sin(y1)
}
function Arg(x, y) {
return atan2(y, x)
}
' | fft -i | /usr/bin/awk '
{
print $1, ($2 + 1) * 0.5, ($3 + 1) * 0.5, 0.6 # scaling
}'
ケーブルの減衰が無視できる場合は簡単で、 例えば下記のようなSPICEシミュレーションができます。
TDR RS1 1 2 50 T1 2 0 3 0 Z0=50 TD=2NS T2 3 0 4 0 Z0=75 TD=10NS RL 3 0 100MEG VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 10MS 100MS) .CONTROL tran 1N 100N plot v(2) .ENDC .END
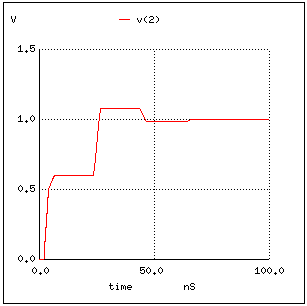
4図 上記SPICEのシミュレーション結果
SPICEには導体抵抗を考慮したLTRAモデルもありますが、 R(抵抗)の周波数特性を考慮していないため、 現実のケーブル伝送による歪を再現できません。
TDR RS1 1 2 50 T1 2 0 3 0 Z0=50 TD=2NS O1 3 0 4 0 TLINE RL 4 0 100MEG VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 10MS 100MS) .MODEL TLINE LTRA(LEN=6 L=3.79e-7 C=6.74e-11 R=5) .CONTROL tran 1N 100N plot v(2) .ENDC .END 例えば、上記のシミュレーションを実行すると、 下記の結果になります。
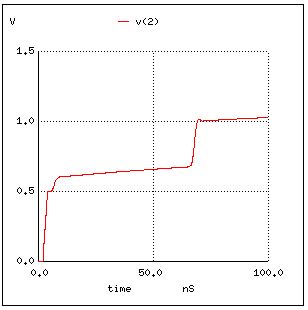
5図 SPICEのLTRAモデルではケーブルの伝送歪を再現できない
平林浩一, 2016-05