伝送特性測定シミュレーションの基礎 (6) - プログラム例 (5)

1. ネットワークアナライザ

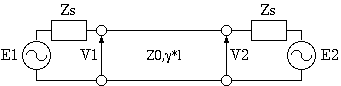
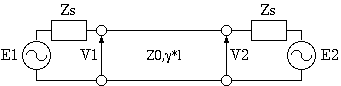
ケーブルのような対称(始端と終端を逆にしても特性が変わらない)回路では S11 = S22, S21 = S12 ですから、 S11 と S21 を計算すればよいのですが、

  S11 = (Zin1 - Zs) / (Zin + Zs)
  S21 = 2 * V2 / E1

ネットワークアナライザを使うときの 最も重要な注意点は反射波と透過波の解釈が TDRや分布定数理論のそれとはまったく違うことです。

TDRや分布定数理論に於ける反射波は 伝搬する電磁波の反射そのものですが、 ネットワークアナライザのS11は 電源から試料に入射した反射波だけでなく、 それが試料終端に進んで、そこで反射した電磁波や、 それがまた試料始端で反射して試料終端で反射し、再度試料始端に戻るという、 無限の入射波と反射波の合計です。 回路的にはネットワークアナライザは 無限の時間が経過したあとの交流理論の世界、 TDRは有限時間の過渡現象理論の世界になります。

同様にS21も無限の時間が経過した後の、 透過波と反射波の合計ですから、 ネットワークアナライザのS パラメータでは 透過波と反射波が分離できません。 この点の誤解はインタネットや宣伝試料、実務書に至るまで、 実に広く存在していますので、 手痛い失敗をしないように注意してください。

こういった誤解を解くためにも、 シミュレーションは有効な手段となります。

2. プログラム例

以下、システムインピーダンス 50 Ωのネットワークアナライザに 3C-2V程度の同軸ケーブルを接続したときの シミュレーションプログラム例です。

ネットワークアナライザの場合も測定機の校正面と試料端接続部分の

• 接続インダクタンス
• 接続キョパシタンス
• ポート延長

また、実務では S11とS21からケーブルの二次定数を求めるプログラムを書いたり することも多いです。

/usr/bin/awk '
BEGIN {
  _Z0 = 75.0		# 特性インピーダンス (Ω)
  _a = 1.373e-6		# 減衰定数 = _a * sqrt(f) + _b * f
  _b = 8.385e-12
  _v = 1/sqrt(2.3)	# 速度係数 (ポリエチレン絶縁)
  _R = 0.0914		# 直流抵抗 (Ω/m)
  _C = 69e-12		# キャパシタンス (F/m)
  l = 5			# 試料長 (m)
  PI = atan2(0, -1)
  Vr = _v
  rs = 50		# ネットワークアナライザのシステムインピーダンス (Ω)
  z0 = _Z0		# 試料の特性インピーダンス (Ω)
  for (i = 1; i <= 100; i += 0.5) {
	f = i * 1e6	# 周波数 (Hz)
	F[i] = f
	w = 2 * PI * f
	a = _a * sqrt(f) + _b * f
	b = w / (2.99792458e8 * Vr) + a
	S11(rs, z0, a, b, l)
	AbsS11[i] = Abs(x, y)
	ArgS11[i] = Arg(x, y)
	S12(rs, z0, a, b, l)
	AbsS21[i] = Abs(x, y)
	ArgS21[i] = Arg(x, y)
  }
  N = i
  exit 0
}
END {
  data = ".1 .45 .6 .90:.6 .95 .6 .90:.1 .45 .1 .40:.6 .95 .1 .40"
  split(data, v, ":")
  data = "abs(S11):arg(S11):Abs(S21):Arg(S21)"
  split(data, yl, ":")
  for (i = 1; i <= 4; i++) {
	print "v", v[i]
	print "x freq. MHz"
	print "y", yl[i]
	for (j = 1; j < N; j++) {
		if (i == 1)
			print F[j], AbsS11[j]
		else if (i == 2)
			print F[j], ArgS11[j]
		else if (i == 3)
			print F[j], AbsS21[j]
		else if (i == 4)
			print F[j], ArgS21[j]
	}
  }
  exit 0
}
# S11 = (Zt - Zs) / (Zt + Zs)
# Zs = z0 = 50 + j*0
function S11(rs, z0, x1, y1, l,  x2, y2) {
  Zin(z0, x1, y1, l, rs, 0)
  x2 = x; y2 = y
  Div(x2 - rs, y2, x2 + rs, y2)
}
# S21 = 2 * V2 / E1
function S12(rs, z0, x1, y1, l,  x2, y2, x3, y3) {
  V2(rs, 0, rs, 0, z0, x1, y1, l)
  x *= 2; y *= 2
}
function coef(z0, xs, ys, xt, yt,  z2) {
  z2 = z0 * z0
  Mul(xs, ys, xt, yt)
  x /= z2; y /= z2
  x += 1
  Div(z0 * x, z0 * y, xs + xt, ys + yt)
}
# V1 = ケーブル送端電圧
# γ = x1 * j*y1
function V1(rs, z0, x1, y1, l,  x2, y2) {
  Zin(z0, x1, y1, l, rs, 0)
  x2 = x; y2 = y
  Div(x2, y2, x2 + rs, y2)
}
# V2 = ケーブル受端電圧
# V2 = 1/2 * 1/(cosh(γ*l) + z0/(Zs+Zt)*(1+(Zs*Zt/z0^2))*sinh(γ*l))
# Zs = xs + j*ys, Zt = xt + j*yt
function V2(xs, ys, xt, yt, z0, x1, y1, l,  a, x2, y2, x3, y3) {
  Cosh(x1 * l, y1 * l)
  x2 = x; y2 = y
  Sinh(x1 * l, y1 * l)
  x3 = x; y3 = y
  coef(z0, xs, ys, xt, yt)
  Mul(x, y, x3, y3)
  Add(x, y, x2, y2)
  Div(1, 0, x, y)
  Mul(x, y, xt, yt)
  Div(x, y, xs + xt, ys + yt)
}
# Zin = (Zt/Z0 + tanh(γ*l) / (1 + (Zt/Z0)*tanh(γ*l)) * Z0
# γ = x1 * j*y1, Zt = x2 + j*y2
function Zin(z0, x1, y1, l, x2, y2,  x3, y3, x4, y4) {
  Tanh(x1 * l, y1 * l)
  x3 = x
  y3 = y
  Mul(x, y, x2 / z0, y2 / z0)
  x4 = x + 1
  y4 = y
  Add(x3, y3, x2 / z0, y2 / z0)
  Div(x, y, x4, y4)
  x *= z0
  y *= z0
}
# Zsc = Z0 * tanh((α + j * β) * l)
function Zsc(z0, x1, y1, l) {
  Tanh(x1 * l, y1 * l)
  x *= z0
  y *= z0
}
# Zoc = Z0 * coth((α + j * β) * l)
function Zoc(z0, x1, y1, l, w) {
  Tanh(x1 * l, y1 * l)
  Div(1, 0, x, y)
  x *= z0
  y *= z0
  error(z0, x1, y1, l, w)
#print " ", y
}
# complex functions
function Add(x1, y1, x2, y2) {
  x = x1 + x2
  y = y1 + y2
}
function Sub(x1, y1, x2, y2) {
  x = x1 - x2
  y = y1 - y2
}
function Mul(x1, y1, x2, y2) {
  x = x1 * x2 - y1 * y2
  y = x1 * y2 + y1 * x2
}
function Div(x1, y1, x2, y2,  r2) {
  r2 = x2 * x2 + y2 * y2
  x = (x1 * x2 + y1 * y2) / r2
  y = (y1 * x2 - x1 * y2) / r2
}
function Exp(x1, y1,  a) {
  a = exp(x1)
  x = a * cos(y1)
  y = a * sin(y1)
}
function Log(x1, y1) {
  x = 0.5 * log(x1 * x1 + y1 * y1)
  y = atan2(y1, x1)
}
function Sqrt(x1, y1,  r, w) {
  x = 0.5 * log(x1 * x1 + y1 * y1) * 0.5
  y = atan2(y1, x1) * 0.5
  a = exp(x)
  x = a * cos(y)
  y = a * sin(y)
}
function Pow(x1, y1, x2, y2,  x3, y3) {
  Log(x1, y1)
  x3 = x
  y3 = y
  Mul(x3, y3, x2, y2)
  Exp(x, y)
}
function Sin(x1, y1,  e, f) {
  e = exp(y1)
  f = 1 / e
  x = 0.5 * cos(x1) * (e - f)
  y = 0.5 * sin(x1) * (e + f)
}
function Cos(x1, y1,  e, f) {
  e = exp(y1)
  f = 1 / e
  x = 0.5 * cos(x1) * (f + e)
  y = 0.5 * sin(x1) * (f - e)
}
function Tan(x1, y1,  e, f, d) {
  e = exp(2 * y1)
  f = 1 / e
  d = cos(2 * x1) + 0.5 * (e + f)
  x = sin(2 * x1) / d
  y = 0.5 * (e - f) / d
}
function Sinh(x1, y1,  e, f) {
  e = exp(x1)
  f = 1 / e
  x = 0.5 * (e - f) * cos(y1)
  y = 0.5 * (e + f) * sin(y1)
}
function Cosh(x1, y1,  e, f) {
  e = exp(x1)
  f = 1 / e
  x = 0.5 * (e + f) * cos(y1)
  y = 0.5 * (e - f) * sin(y1)
}
function Tanh(x1, y1,  e, f, d) {
  e = exp(2 * x1)
  f = 1 / e
  d = 0.5 * (e + f) + cos(2 * y1)
  if (d == 0) {
	e = exp(x1)
	f = 1 / e
	x = 0
	y = (e + f) * sin(y1)
  }
  else {
	x = 0.5 * (e - f) / d
	y = sin(2 * y1) / d
  }
}
function Atanh(x1, y1) {
  Div(1 + x1, y1, 1 - x1, -y1)
  Log(x, y)
  x *= 0.5
  y *= 0.5
}
function Abs(x, y) {
  return sqrt(x * x + y * y)
}
function Arg(x, y) {
  return atan2(y, x)
}
'

3. 注

3.1. 注１-

平林浩一, 2016-05