集合より線の外径

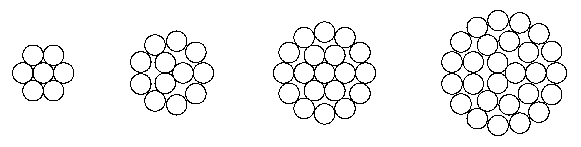
電線の導体には単線(solid wire)を呼ばれる１本の銅線と より線(stranded wire)と呼ばれる 複数の銅線をより合わせたものが使われますが、 より線については、１図のように素線を同心円上に配列した同心より線と、 素線の位置が不規則な集合より線(bunch strand)があります。 より線に使われる銅線の断面は曲げ方法の自由度が高く、 引き抜き加工に使われるダイス(wire drawing dies)が作りやすい円形が普通です。

１図 同心より線の例

同心より線の利点は外周が円に近く、 絶縁体が最低限の厚さで済むことですが、 その代償は１層づつ撚機でより合わせるため工程が増えることです。 一方、集合より線は全素線をまとめて一度にねじり合わせるもので、 安価で素線本数も自由に選べるという利点もあって、 柔軟性を必要とする電線で多用されています。

むろん、強引にねじってしまう以上、 素線の材料が銅など塑性変形できるである必要があって、 バネ性のある鋼線などで集合より線を作ることはできません。

比較項目	同心撚	集合撚
断面外周形状	円形	非円形
撚方向	層毎に逆	全素線同方向
工程数	層数と同じ	１工程
素線数	制限がある	自由
コスト	高価	安価

1. 集合より線の外径近似値

集合線の素線の位置や外径がどうなるかは運任せで、 しかも、長さ方向にそって一様になる保証もありません。 それでも、集合工程や絶縁被覆の押出工程の治具の選定や 電気特性の概算値を求める場合など、 その外径を知らなければならない場合が多く、 下記の近似式がよく知られています。 (* は乗算記号、/ は除算記号、sqrt(n) は n の平方根 (square root)の意味で、 プログラミング言語の記述で良く使われます。)

  D = 1.155 * d * sqrt(n)          (1)
  ここに、
	D = 集合線の外径
	d = 素線径
	n = 素線数

この式の用途としては、 例えば、集合より線を作る集合機で使われるダイス(dies)とか、 集合より線に絶縁体を被覆する押出機のニップル(nipple)の内径などは、 素線のより繋ぎによる外径の増加を考慮して (1) 式で得られた値に素線１本分を加えた値を使うといった使いかた をするわけです。

以下、この近似式がどうやって求められたのかを考えてみますが、 私自身は、この式が業界に定着した事情を知りませんので、 (1) 式の妥当性を考えてみることにして、それには、 まず、集合線の外径とは何かを考えなければなりません。

集合線の外径の定義として最も素直なのは、 集合線が入る最小の円の直径です。 ただ、これは素線の配列の仕方によって変化しますから、 数学的には「n 個の単位円盤を詰め込むことのできる最小の円の半径は何か？」 といった円の円への詰め込み問題になって、 そう簡単ではありません。(注１)

つまり、集合線の外径の最小値は 集合素線径に等しい円を詰め込むことができる最小の円になりますが、 これまでに知られている結果については

The best known packings of equal circles in a circle (complete up to N = 2600)

によくまとめられています。

一般の集合線の外径はこの値より大きくなりますが、 １図の同心より線の場合は、各層間の素線数に

  Mm+1 = Mm + 6           (2)
  ここに、
	Mm = 第 m 層の素線数
	Mm+1 = 第 m+1 層の素線数
	m = 2, 3, 4, ..

  N = M0 + M + (M + 6) + (M + 12) + (M+ 18) + .. + (M + 6*(k - 1))
    = M0 + k * (M + 3 * (k - 1))                          (3)
  ここに、
	N = 全素線数
	M0 = １層目(中心)素線数 (1, 2, 3, .. 5)
	M = ２層目の素線数 (6 <= M <= 12, M0 依存)
	k = 層数 - 1

  D = D0 + 2 * d * (k - 1)
  ここに、
	D = 外径
	D0 = １層目の外径 (d <= D0 <= 3 * d, １層目(中心)素線数依存)
	   = d * (1 + 1 / sin(π / M0))                    (4)
	   ∼ d * (1 + M0 / π)  .. (1 << M0)               (5)

  N ∼ 3 * k^2
  D ∼ 2 * d * k

  D ∼ 2 / sqrt(3) * d * sqrt(N) ∼ 1.155 * sqrt(N) * d      (6)

一方、 n 個の直径 d の円を直径 D の円に詰め込んだときの d 円の密度を ρ とすれば

  ρ = N * d^2 / D^2

  D = d * sqrt(N / ρ)

直径 d の円を無限平面に敷き詰める場合、 密度が最大になるのは、３つの円をお互いに接触させた場合で、 左図の３つの円の中心を結ぶ三角形の面積 d^2*sqrt(3)/4 に占める 斜線部分の面積 π/2/sqrt(3) の比ですから、

ρmax = π / (2 * sqrt(3)) ∼ 0.90690..

になります。

直径 d の円を直径 D の円に詰め込む場合の密度はこの値 0.90690.. を越えることができませんが、 D が無限に大きくなったときの極限値が ρmax になります。

以下、 この極限値と(組み合せ論数学)的最小値、通常使われる近似値の比較図を用意しました。

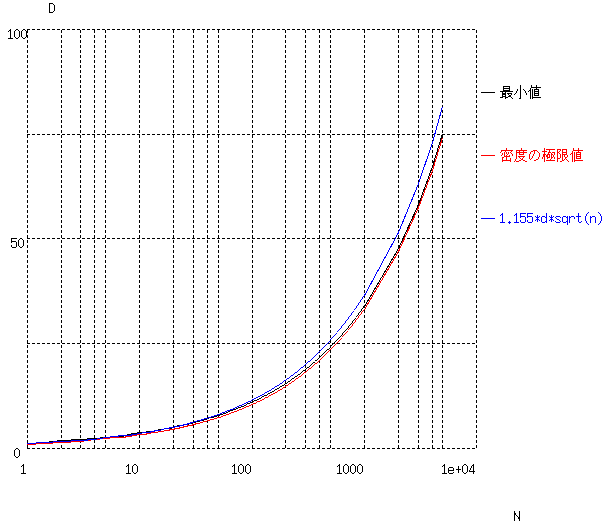
(1) 式は素線数が大きくなるにつれて、過大評価になることがわかります。

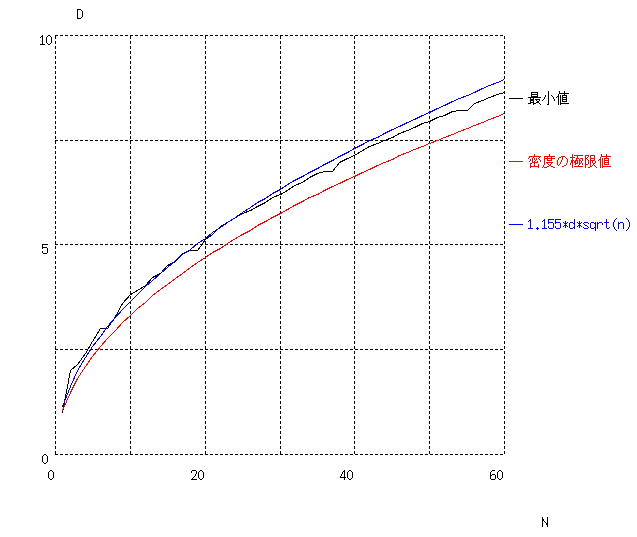
素線数が小さい場合は (1) 式と実際の最小値が良い近似になっていて、 素線数が大きい場合と比べて無駄な空間が増えることがわかります。

注１ - 円の円への詰め込み問題

数学的には Math. Mag.40(1967)65-71, Math. Mag.44(1971)134-139) など古くからの研究対象です。

注２ - 同心より線の層間素線数差

隣接する２層の素線数の差は

  N(m+1) - N(m) = d / sin(π/(n + 6) - d / (π / n)
	∼ 6 * d / π ∼ 2 D - 0.090 * d

  D(n+6) - D(n) ∼ 2 * d - 0.090 * d

層間素線数差を直接計算する場合は、

同心より線の外径の (1) 式から

  dN = π * (1 / asin(d/D) - 1 / asin((d/D) / (1 + 2 * (d/D))))
  ここに、
	dN = 層間素線数増加量 (素線本数差)
	d = 素線径
	D = 層心径
	asin(x) = atan(x / sqrt(1 - x * x))

  dN ∼ 2 * π ∼ 6.29