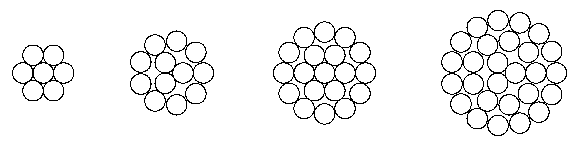
断面が円形の導体や絶縁電線の中心を何層かの同心円上に配置して 撚合わせた同心より構造は多くの導体やケーブルで使われていますが、 こういった同心より線の幾何学的性質について、 より合わせる素線の外径がすべて同じ場合を考えます。 (注0)

1図 同心より線の例
1図は典型的な同心より構造の例ですが、 完成したより線の外径(外接円直径)が最小になるような素線の層配分を選ぶのが普通で、 下表ような層構成がよく使われています。中心層が 6 本未満なのは、6 本になると、 その中に素線が 1 つ入ってしまうためです。
線心数 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ---------------------------------------------------------------- 第1層 1 1 1 2 2 3 3 4 4 5 5 6 1 1 1 1 1 2 2 第2層 6 7 8 8 9 9 10 10 11 11 12 12 6 6 7 7 8 8 8 第3層 12 13 13 14 14 14 15 線心数 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 ---------------------------------------------------------------- 第1層 2 2 3 3 4 4 4 5 5 5 6 1 1 1 1 1 1 1 2 第2層 9 9 9 10 10 10 11 11 11 12 12 6 6 6 7 7 7 8 8 第3層 15 16 16 16 16 17 17 17 18 18 18 12 12 13 13 14 14 14 14 第4層 18 19 19 19 19 20 20 20以下、この標準線心配列が出来た理由の根拠にも関係する話題になりますが、 素線径で量子化される組み合わせ問題ですから、 無駄な隙間が生ずる線心数もあって、 その場合は中心に近い層の外径を増やすように 繊維などの介在(filler)を入れます。
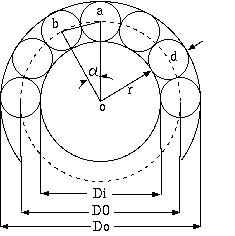
2図 素線断面の円近似による素線径、素線数、層径の関係
撚ピッチが大きいときは、 素線の中心軸と撚の中心軸が平行に近く、 撚の断面に於ける素線断面がほぼ円形になりますから、 2図のように、直径 d の素線 N 本を隙間なく並べる場合は、 次式が古くから使われてきました。(注1)
D0 = d / sin(π / N) (1) ここに、 D0 = 層心径 (pich diamter) d = 素線径 N = 素線数 π = 3.1415..層外径と層内径は
Do = D0 + d = d * (1 + d / sin(π / N)) Di = D0 - d ここに D = 層外径 Di = 層内径
sin(x) の級数展開
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + .. (-∞ < x < ∞)の最初の項だけを使えば
Do ∼ d * (1 + N / π) .. (1 << N) (2)の近似式が得られ、これは層の ピッチ円を直線に伸ばして、 外径 d の素線を N 本並べた場合になりますが、 素線数が 10 を越えると誤差 1 % 以下、 わずか 3 本でも誤差 10 % を切ります。
(1) 式は素線を撚合わせない場合ですが、 撚合わせると素線断面が円ではなくなって、 隣接素線間の距離が増加し、 D の値はもっと大きくなりますから、 例えば、素線 1 本の周囲に素線 6 本という配置では中心の 1 本が周囲の 6 本と密着できず、 7 心同心より線が成立するはずがないということに気づきます。 つまり、素線断面の円近似はごく限られた条件でしか使えません。
円柱を斜めに切断すると断面は楕円になりますから、 撚ピッチがあまり小さくなければ、素線の断面を楕円で近似できて、 より精度の高い近似式が得られます。
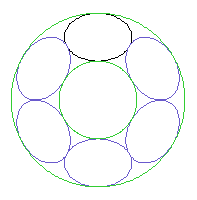
3図 素線断面の楕円近似による素線 6 本の配置例
素線断面を楕円で近似したときの、 素線径、素線数、層径の関係は次式のようになります。 (注2)
r = √((a * m)^2 + b^2) (3) ここに、 r = 層心円(素線中心の配置円)の半径 b = d / 2 = 楕円の短径/2 (素線配置円の円周と直行方向) a = k * b = 楕円の長径/2 (素線配置円の円周方向) ψ = π / N α = π / 2 - ψ m = tan(α) d = 素線径 N = 素線数 k = 撚込係数 (1 <= k) = 1 ピッチあたりの素線長 / 1 ピッチの長さ
k は素線長を撚の長さで規格化した値で、 単位長の撚線を作るのに必要な素線の長さになり、 撚構造では重要な役割を果たします。 私は撚込係数と呼んできましたが、 ロープ分野ではより込み率(in-out ratio)と呼び、 長さ 1 (m) の撚線を作るには、長さ k (m) の素線を必要とするという意味です。 微分幾何学的には撚の 1 ピッチあたり 1/k 回転の捻れを生ずることになります。
層心円の半径がわかれば、層外径と層内径は簡単に得られます。 撚合わせても層の厚さは変化しないことに注意してください。
Di = (r - b) * 2 Do = (Di + b) * 2 ここに、 Di = 撚素線の内接円直径 (層内径) D2 = 撚素線の外接円直径 (層外径)
k = 1 だと素線断面が円になって (1) 式と一致し、 k が 1 に近いとき、Do, Di, r の値は k に比例して増加します。
通常の撚構造の撚ピッチは層心径の 10 倍以上で、 15 倍程度を選ぶことが多いのですが、 3図は d = 1, N = 6, k = 1.1 の場合で、 撚ピッチが層心径の 15 倍(撚の角度 65 度、)ですから、 通常の撚構造でも (1) 式の誤差が無視できず (3) 式が必要になることがあります。
なお、軟銅線とか柔軟な絶縁体を使った絶縁導体では、 塑性変形しますから、ごまかせるケースもあります。
撚の角度が 45 度 (撚込係数が √2) 以上だと素線をより合わせる感覚、 45 度未満だと素線を巻き付ける感覚になりますが、 素線断面の形状も撚角 45 度あたりを堺にして、 楕円近似が使えず、微分幾何学的計算が必要になります。 (注3)
計算自体はかなり面倒ですが、 撚線の場合は撚素線の中心線の形状が 常螺旋(helix)になるため、 幾何学量が三角関数だけで表現できて、 半径 a の素線 N 本の中心を同一円周上に密接配置したときの 層心円半径は次ぎのようになります。
r = a / √(1 + (cos(ψ))^2 * (k^2 - 1)) / sin(ψ) (4)
sin(2*ψ) = 2/(k^2 - 1)*(π/N - ψ) (5)
ここに
a = 素線半径
k = 素線の撚込係数
N = 撚素線数
r = 撚の層心半径 (ピッチ半径)
最初に (5) 式から ψ を求めて、
次ぎに (4) 式から層心半径を求めることになりますが、
(5) 式は解析的に解けませんので、
数値解法を使います。
層心半径がわかれば、層の厚さは 2 * a ですから、 撚層の外径と内径(コア径)がわかります。
Di = (r - a) * 2 Do = (r + a) * 2 ここに、 Di = 内接円外径 (層内径) Do = 外接円外径 (層外径)
以下、外径 1 mm の素線 6 本を例に、 撚ピッチを小さくしていったときの素線断面の形状変化、 撚の外径変化計算してみた結果です。 (注4)
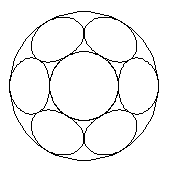
4図 撚込係数 √(2) (撚角 45 度)
4図は素線径 1 の素線 6 本を撚込係数 `√(2) で撚合わせた状態ですが、 撚の角度は 45 度ですから、撚り合わせと巻き付けの境界で、 素線断面も楕円とは言いにくくなっています。 外径は 3.717 mm、内径は 1.717 mm です。
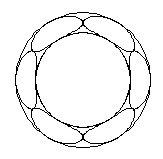
5図 撚込係数 3 ((撚角 10.03 度)
撚込係数が 3 になると、撚角 10.04 度ですから、 撚るというより巻き付けるという状態になって、素線断面は楕円とは大きく異なります。 外径 1 mm の素線 6 本でも外径は 6.730 mm、内径は 4.730 mm になります。
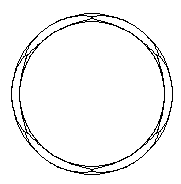
6図 撚込係数 10 (撚角 5.739 度で)
撚込係数が 10 になると、撚角は 5.739 度ですから、 外径 1 mm の素線 6 本でも外径は 20.1 mm、内径は 18.1 mm になります。
素線径が同じでない場合は、 個々のケースについて数値解法で素線中心位置を求めることになって、 コンピュータの出番になります。
2図の三角形 abo に注目すると、 角度 α は 2*π/N (radian) ですから、余弦定理(Law of Cosines)を使って
d^2 = r^2 + r^2 - 2 * r * cos(α) ここに、 d = 素線径 c = a-b 間の長さ r = 層半径 (pitch diameter 素線配置円の半径)r を求めるには倍角公式(Double Angle Formulas)を使って
r^2 = d^2 / (2 - 2 * cos(2 * π / N)
= d^2 / (4 * sin(π/ N)^2)
r = d / (2 * sin(π / N) (1.1)
素線の中心軸は数学的に自然な常螺旋ですから、(1) の外径公式より (1.1) 式を強調するほうが良いし、応用範囲も広いと思います。
なお、三角形 oab を a-b の中点と o を結ぶ直線で左右対称な直角三角形に 分ければ、もっと簡単に (1.1) 式が得られますし、手間は増えますが、 正弦公式(Law of Sines)と半角公式(Half Angle Formulas)の組合せも使えます。
解析幾何学的計算を容易にするために、 3図の一番上の素線(楕円)の中心を x-y 座標の原点にして、 楕円の長軸を 2*a、短軸を 2*b とすれば、楕円と x 軸の交点は (-a, 0) と (a, 0)、y 軸との交点は (0, b) と (0, -b) で、 撚の中心は (x1, y1) になります。 楕円の中心を同心円上に密接配置したとき、 隣の楕円と接するのが撚の中心を通る楕円の接線ですから。
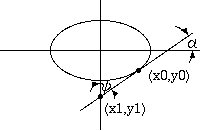
5図 楕円上の接点 (x0, y0) を通る接線
楕円の方程式
x^2 / a^2 + y^2 / b^2 = 1 (2.1) ここに a = 長軸 / 2 b = 短軸 / 2 (素線外径 / 2)と楕円上の接点 (x0, y0) を通る接線の方程式
x * x0 / a + y * y0 / b = 1 (2.2)から接点座標 (x0, y0) を計算すると、
x0 = (a^2*m*r+a*√(a^2*m^2*r^2-(b^2+a^2*m^2)*(r^2-b^2))/(b^2+a^2*m^2) y0 = m * X0 - √(a^2 * m^2 + b^2) ここに、 ψ = π / N α = &pi / 2 - ψ m = tan(α)これで、接線の方程式が決まりますから、 この接線と y 軸の交点 (x1, y1) が決まって、
x1 = 0 y1 = -√(a^2 * m^2 + b^2)層心円の半径が √(a^2 * m^2 + b^2) になることがわかります。
素線の形状は円柱で、円柱を斜めに切ると切断面は楕円になりますが、 その楕円の短軸の長さは素線の直径 b と同じです。 楕円の長軸の長さ a は撚の角度を θ とすると
a = b / sin(θ) = b * k ここに θ = 素線の撚角 (撚の中心軸と素線の中心軸の角度) k = 素線の撚込係数 (素線長 / 撚の長さ)
曲げと捻り(平面から離す曲げ)という二つの操作で、いかなる空間曲線も作れますが、 微分幾何学は曲率(cuvation)と捩率(tortion) という局所的な微分量を使って空間曲線や空間曲面を解析する手法です。 微分幾何学の計算はかなり複雑ですが、電線やロープの基本となる常螺旋(helix)では 形状を決定する曲率と捩率の両方が一定 になるため比較的簡単な計算で済みます。
微分幾何学の対象・応用領域はかなり広く、 それらの解説も簡単ではありませんが、 電線を素材にした解説については、 私が現役時代に書いた解説がありますので、 微分幾何学のテキストを見ながら参照していただくと、 多少はわかりやすくなるかもしれません。 少なくとも、実際に動くプログラム例は役にたつと思います。
この解説では電線やロープなど、撚込係数が 1 に近い場合を想定していますから、 素線を撚合わせるという発想で、 よりの長さ方向を z 軸、より断面を x-y 軸という座標系で考えていますが、 コイルばね(spling)の場合は k 値が非常に大きいので、撚るというより 巻き付けるという製法になりますから、コイルを横から見た座標軸、 バネの巻き付け中心を原点として、巻き付け軸を y 軸に取ると、 撚線で微分幾何学的計算になるケースが円近似や楕円近似で済みます。
縦から見るか横から見るかで素線断面の形状が変わりますから、 解析手法も変わって、同じ常螺旋の解析が別の道を歩むことになりました。
平林 浩一 2020-10-20