整列巻き

太いケーブルをドラムに巻き付ける場合は、ケーブルが傷まないように、 ドラムに隙間なく巻き付ける必要があって、 ドラムとケーブルの外径から、 巻き付けピッチと撚込係数を求める計算が必要になります。

1. 円近似

ドラム径に対してケーブル径が十分小さい、 つまり、b << a なら、 ドラムの中心軸を通る平面に於けるケーブル断面形状は円に近づきます。 この場合は極めて簡単で、

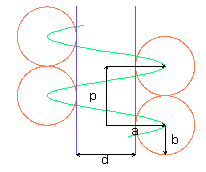
  a = ケーブルのピッチ半径 (m)
  b = ケーブル半径 (m)
  d = 2 * (a - b)
    = ドラム径 (m)
  p = ケーブル巻き付けピッチ (m)
  k = 巻き付けケーブルの撚込係数
    = １巻きのケーブル長 / 巻き付けピッチ

  p = 2*b                        (1.1)
  k = sqrt(1 + (π*a/b)^2)       (1.2)

2. 楕円近似

実際には巻き付け中心軸を通る平面に置けるケーブルの断面は円ではなくて、 巻き付けピッチが増加し、撚込係数は減少します。

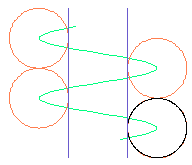
ドラム径に対してケーブル径が無視できなくなると ドラムの中心軸を通る平面に於けるケーブル断面形状は楕円に近くなりますが、 この近似値としての楕円は円柱としてのケーブルを、 ケーブル中心軸と撚角 θ をなす平面で切断した断面ですから、 次ぎの関係が得られます。 (注２)

  p = 2*b/sqrt(1 - (b/(2*π*a))^2)      (2.1)
  k = sqrt(1 + (2*π*a/p)^2)            (2.2)

3. 微分幾何学的計算

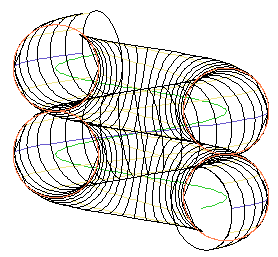
さらに、巻き付けるケーブルの曲がりと捻れを考慮すると、 微分幾何学的計算が必要になって、 下記の結果が得られます。

  p = 2*π*a*sqrt(sin(2*θ)/(2*π - θ))                       (3.1)
  k = sqrt(1 + 2*(π - θ)/sin(2*θ))                          (3.2)
  ここに、
	(b/(a*sin(θ))^2 = 1 + 2(π - θ)*cos(θ)^2/sin(2*θ)  (3.3)

  1 + 2(π - θ)*cos(θ)^2/sin(2*θ) - (b/(a*sin(θ))^2 = 0

上図は巻き付けたケーブルの 1.7 ピッチ程度を表示したもので、 緑線が巻き付けたケーブルの中心、 赤線は撚の中心を通る平面を通る撚合わせたケーブルの断面、 黒線は撚合わせたケーブルの表面形状です。

こういった計算については ワイヤ・ケーブルの微分幾何学 をご欄ください。

なお、柔軟なケーブルの場合は巻き付けると断面が偏平に歪み、 見掛けの幅が大きく、厚さが小さくなりますので、 上記で得られた巻き付けピッチより大きくなります。

4. 注

4.1 注１ - 円近似の撚込係数

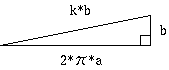巻き付けるケーブル中心の常螺旋は 伸縮することなしに平面に展開できる可展面ですから、 1 ピッチ分を平面に展開すれば、 撚込係数 k の値はピタゴラスの定理

  (k*b)^2 = (2*π*a)^2 + b^2

4.2 注２ - 楕円近似

巻き付けるケーブルのピッチ円を含む断面を平面で近似すると、

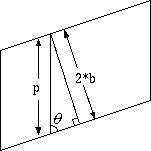
  sin(θ) = 2*b/p            (4.2.1)
  ここに
	θ = 撚角 (撚の中心軸とピッチ円の角度)
	b = 巻き付けるケーブルの半径 (m)
	p = 密巻きピッチ (m)

撚角 θ については巻き付けるケーブルの中心になる常螺旋の 1 ピッチ分を 平面に展開すれば、

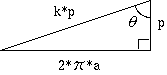
  tan(θ) = p/2*π*a             (4.2.2)

あとは (4.2.1), (4.2.2) から θ を消去して p を求めれば良いのですが、

  tan(θ) = sin(θ)/cos(θ) = sin(θ)/sqrt(1 - sin(θ)^2)

に注意すれば

  p = 2*b/sqrt(1 - (b/(2*π*a)^2)     (4.2.3)

  k = sqrt(1 + (2*π*a/p)^2)        (4.2.4)

4.3 注３ - 誤差

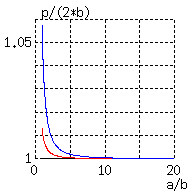
いずれの場合も、巻き付けピッチ p は a/b の関数になりますから p(a/b) の値を３つの近似について計算してみると、 左図のようになって、 円近似が使えるのは 10 < a/b 程度、 楕円近似なら 5 < a/b 程度になることがわかります。