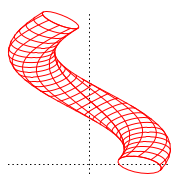
 β = 0 を曲面の法線方向にとれば、c1 の半径 b の主法線ベクトルを求めることで素
線表面の形状が決まります。
β = 0 を曲面の法線方向にとれば、c1 の半径 b の主法線ベクトルを求めることで素
線表面の形状が決まります。
無限に細い針金のあちこちを曲げたり捻ったりすれば、 いかなる空間曲線も作れますが、 微分幾何学(differential geometry)は 空間曲線上の曲率(curvature 曲げ)と捻率(tortion 捻り)という 微分量(無限小区間に於ける変化量)を使って、 空間曲線や空間曲面を解析する手法です。 曲率は直線からの離れかた、 捻率は平面からの離れかたですが、 空間曲線の場所によって、 曲がりかたも捻れかたも違いますから、 微分量として考える必要があります。 空間曲面は空間曲線の移動で作れます。
ケーブルで最もよく使われる構造は 円形断面を持つ素線を撚合わせたものですが、 その幾何学的構造の把握には初歩的な微分幾何学が必要で、 以下、微分幾何学的解析結果の要点を説明します。 (注1)
ここでは、 ケーブル素線がゴムのように伸び縮みする弾性体と仮定していることに 注意してください。なお、解説中の図は awk で座標を計算した結果を gnuplot で作図したもので、気軽に実験できるように、ソースコードを付けておきます。
ケーブルを構成する素線はすべて、素線の中心線の接線に直交した円形断面を持ちます が、この表面形状を管状曲面と呼ぶことにすれば、 すべての素線は他の素線に一定の曲率と一定の捻率で巻き付けられていますから、 素線の中心曲線は1つ前の素線の管状曲面上にあって、 下記の手法ですべての素線形状(素線の中心曲線と表面曲面)を決定することができます。
[ tn ] [ cos(φn) -sin(φn)*sin(αn) sin(φn)*cos(αn) ] [ tm ] [ en ] = [ 0 -cos(αn) -sin(αn) ] [ em ] [ dn ] [ sin(φn) cos(φn)*sin(αn) -cos(φn)*cos(αn) ] [ dm ] ここに tn = [tnx tny tnz] (n 次の素線の中心曲線の接線ベクトル) en = [enx, eny, enz] (n 次の主法線ベクトル) dn = [dnx dny dnz] (n 次の従法線ベクトル) あるいは tn = cos(φn)*tm - sin(φn)*sin(αn)*em + sin(φn)*cos(αn)*dm en = -cos(αn)*em - sin(αn)*dm dn = sin(φn)*tm + cos(φn)*sin(αn)*em - sin(φn)*cos(αn)*dm ここに、 φn = 撚角(lay angle) = atan(√(kn^2 - 1)) kn = 撚込係数 (素線長 / 素線を巻き付ける管状曲面の中心線の長さ) = ストランド作成時の(1ピッチあたり素線長/撚ピッチ) αn = 位相(phase) n = 0, 1, 2, 3, .. m = n - 1 [tnx tny tnz] = n 次の中心曲線の接線ベクトル [enx eny enz] = n 次の中心曲線の主法線ベクトル [dnx dny dnz] = n 次の中心曲線の従法線ベクトル撚角(φn)は n 次の素線中心の接線と m 次の素線中心の接線の角度、 位相(αn)は中心 曲線を含む管状曲面の主法線と曲線間の角度です。
また、n 次の管状曲面上で一定の撚込係数 kn を持つ曲線は管状曲面に下記の制約を課 すことで得られることが証明できますから、ケーブルの中心曲線から出発して、順次、 tn, en, dn を求めることができます。
αn/αm = am/an*√((kn^2 - 1)/(1 - 1/km^2)) ここに、 kn = n 次の素線の撚込係数 km = m 次の素線の撚込係数 kn = n 次の素線の撚込係数 φn = atan((√(kn^2 - 1) + Fn)/hn) ここに、 hn = √(En*Gn - Fn^2) En, Fn, Gn = n 次管状曲面の第一基本量(1st fundamental quantities)En, Fn, Gn は微分幾何学で曲面の第一基本量と呼ばれるもので、 hn は n 次素線表面 上で2つの独立したベクトルの外積、Fn は内積で、この2つが素線表面曲面を決める ことになります。この2つのベクトルの選択次第で第一基本量も変化しますが、ここで は、n 次素線中心を元に n 次素線表面を求める場合は曲率線の接線ベクトルと法線ベ クトルを使い、撚込係数あるいは撚角で制限される素線表面上の曲線、すなわち、次の 素線中心曲線を求める場合はその曲線の接線と主法線ベクトルを使うことにします。た だ、いずれの計算もかなり面倒で(注1)、以下の解説では、この計 算の詳細には触れません。詳細は微分幾何学の解説書を参照してください。
これらのベクトルが得られれば、素線表面は素線の中心曲線から素線の半径を長さとし た主法線ベクトルで表すことができて、cm を m (= n - 1) 次の中心曲線、 sm, sn を m 次と n 次の表面曲面とすれば、
sn = cm + an*cos(αn) + an*sin(αn) ここに、 sn = n 次の素線表面曲線 cm = m 次の素線中心曲線 an = n 次の素線半径を長さとした cm の主法線ベクトルとなり、その次の次数の素線中心は素線表面曲面を次の素線半径分拡大した管状曲面を その次の次数の素線の撚込係数(in-out lay ratio, take-up factor)で制限した曲線 になりますから、計算は繁雑ですが、微分幾何学の曲面の基本量を使って、順次、 素線中心と素線表面の形状を計算してゆくことができます。
また、素線の曲率や捻率を求めたい場合もありますが、 この場合は微分幾何学で曲面の第二基本量と呼ばれる値と概念が必要で、 ここでは、いくつかの結果だけを記述しておきます。
以下、0 次の中心曲線を z 軸方向の直線として、わかりやすいように、α0 = α、 α1 = β、α2 = γ と置き換えて、tn, en, dn を 2 次まで計算すると、次のように なります。
t0 = [ 0 0 1 ] e0 = [ 1 0 0 ] d0 = [ 0 1 0 ]
t1 = [ -sin(φ1)*sin(α) sin(φ1)*cos(α) sin(φ1) ]
e1 = [ -cos(α) -sin(α) 0 ]
d1 = [ cos(φ1)*sin(α) -cos(φ1)*cos(α) sin(φ1) ]
[ -sin(φ1)*cos(φ2)*sin(α)+sin(φ2)*(cos(α)*sin(β)+cos(φ1)*sin(α)*cos(β)) ]
t2 = [ sin(φ1)*cos(φ2)*cos(α)+sin(φ2)*(sin(α)*sin(β)+cos(φ1)*cos(α)*cos(β)) ]
[ cos(φ1)*cos(φ2)+sin(φ1)*sin(φ2)*cos(β) ]
[ cos(α)*cos(β)+cos(φ1)*sin(α)*sin(β) ]
e2 = [ sin(α)*cos(β)+cos(φ1)*cos(α)*sin(β) ]
[ -sin(φ1)*sin(β) ]
[ -sin(φ1)*sin(φ2)*sin(α)-cos(φ2)*(cos(α)*sin(β)+cos(φ1)*sin(α)*cos(β) ]
d2 = [ sin(φ1)*sin(φ2)*cos(α)+cos(φ2)*(sin(α)*sin(β)-cos(φ1)*cos(α)*cos(β) ]
[ cos(φ1)*sin(φ2)-sin(φ1)*cos(φ2)*cos(β) ]
3 次の e3 はかなり複雑になって、下記 s3 曲面の計算結果として記述します。
以下、a1 = a, a2 = b, a3 = c, .. , α0 = α、α1 = β、α2 = γ、.. として、 3 次の素線表面まで中心曲線と表面曲面を計算すると、次のようになります。
右手座標でケーブルの中心曲線を Z 軸方向にとることにすれば、
c0x = 0 c0y = 0 c0z = 任意の値
α = 0 を x 軸、撚の方向を z 軸にとると、 c0 直線の法線方向半径 a の曲面は下記のようになります。
s1x = a*cos(α) s1y = a*sin(α) s1z = 任意の値 ここに、 a = 中心素線の半径 α = 位相 .. c0 直線の従法線ベクトルの X 軸からの回転角 tan(α) = s0y/s0x
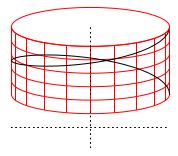
座標軸の左右方向が x 軸、上下方向が z 軸です。 α = 0 から &alpha = 2*π までの 1 ピッチを描画しています。
s0 曲面上の曲線を k1 が一定になるように制限すると下記のようになります。
c1x = s1x c1y = s1y c1z = a/√(k1^2 - 1)*(α - α0) φ1 = atan(√(k1^2 - 1)) ここに、 k1 = 中心ストランドの外側素線の撚込係数 α0 = (z = 0 に於ける)初期位相 φ1 = 撚角 (z 軸と c1 の間の角度)これは、s1 曲面上で外側素線の撚込係数
k1 = √(1 + (2*π*a/p)^2) ここに、 k1 = 中心ストランドの外側素線の撚込係数 p = 中心ストランドの外側素線の巻き付けピッチが一定になるように制限した値であることに注意してください。c0 曲面で不定だった z の値が決まります
αが正方向に増加すれば Z 撚、負方向に増加すれば S 撚で、下記の関係があります。
cos(φ1) = 1/k1 sin(φ1) = √(k1^2 - 1)/k φ1 > 0 なら Z 撚、φ1 < 0 なら S 撚
 β = 0 を曲面の法線方向にとれば、c1 の半径 b の主法線ベクトルを求めることで素
線表面の形状が決まります。
β = 0 を曲面の法線方向にとれば、c1 の半径 b の主法線ベクトルを求めることで素
線表面の形状が決まります。
s2x = -b*e2x + c1x s2y = -b*e2y + c1y s2z = -b*e2y + c1z e2x = cos(α)*cos(β) - cos(φ1)*sin(α)*sin(β) e2y = sin(α)*cos(β) - cos(φ1)*cos(α)*sin(β) e2z = -sin(φ1)*sin(β) ここに、 tan(φ1) = √(k1^2 - 1) β = 位相 .. c1 直線の従法線ベクトルの回転角
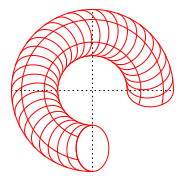
s2 曲面上の曲線を k2 が一定になるように制限すると、αとβが独立ではなくなって、 下記のようになります。
c2x = -b*e2x + c1x c2y = -b*e2y + c1y c2z = -b*e2y + c1z e2x = cos(α)*cos(β) - cos(φ1)*sin(α)*sin(β) e2y = sin(α)*cos(β) - cos(φ1)*cos(α)*sin(β) e2z = -sin(φ1)*sin(β) β = a/b/sin(φ1)*√(k2^2 - 1)*α + β0 ここに、 k2 = 中心素線の外側ストランドの外側素線の撚込係数 β0 = (z = 0 に於ける)初期位相 (β0 = 0 は s2 曲面の法線方向)β = 0 は中心曲線に一番近い場所、β = π なら中心曲線から最も離れた場所である ことに注意してください。
 c2 の半径 c の法線ベクトルから外側ストランドの外側素線の表面曲面が得られます。
c2 の半径 c の法線ベクトルから外側ストランドの外側素線の表面曲面が得られます。
s3x = -c*e3x + c2x s3y = -c*e3y + c2y s3z = -c*e3y + c2z e3x = -(cos(α)*cos(β)-cos(φ1)*sin(α)*sin(β))*cos(γ) +(sin(φ1)*sin(φ2)sin(α) +cos(φ2)*(cos(α)sin(β)+cos(φ1)*sin(α)*cos(β))*sin(γ) e3y = -(sin(α)*cos(β)+cos(φ1)*cos(α)*sin(β))*cos(γ) -(sin(φ1)*sin(φ2)cos(α) -cos(φ2)*(sin(α)sin(β)-cos(φ1)*cos(α)*cos(β))*sin(γ) e3z = sin(φ1)*sin(β)*cos(γ) -(cos(φ1)*sin(φ2)-sin(φ1)*cos(φ2)*cos(β))*sin(γ) ここに、 γ = 位相 .. c2 直線の従法線ベクトルの回転角 (γ = 0 も s3 曲面の法線方向にとります) φ2 = c1 直線と c2 直線の角度 tan(φ2) = (√(k2^2 - 1) + b/a*cos(φ1)*sin(φ1)) / (1 - b/a*(sin(φ1))^2*cos(β))
s3 曲面上の曲線を k3 が一定になるように制限すると、下記の関係が得られます。
γ = b/c/(sin(φ2) - b/a*cos(φ1)*sin(φ1)*cos(φ2)) *(1 - b/a*(sin(φ1))^2*cos(β))*√(k3^2 - 1)*β + γ0 ここに、 k3 = 外側ストランドの外側ストランドの外側素線の撚込係数 γ0 = 初期位相 (γ0 = 0 はφ s3曲面の法線方向)s3 曲面の式と組み合わせると、中心曲線 c3 が得られます。
3次元の曲面を2次元で作図するとき、曲面上の曲率線を一定間隔でプロットすると曲 面の把握が容易になりますから、曲率線を決める条件を求めると下記のようになります。
β = a/b/sin(φ1)*√(k2^2 - 1)*α γ = cos(φ2)/(1 - b/a/sin(φ1)*cos(β)) *(b/a*cos(φ1)*sin(φ1)/√(k2^2 - 1)) + 1)*β例えば s2 表面なら、βを一定にしてαを変化させたものと、αを一定にしてβを変化 させたものの2つがあります。
作図の簡単な平行投影で作図すると、例えば、X 平面で
enx < 0 陽線 (x 軸方向で外向き) enx = 0 輪郭線 enx < 0 隠線 ((x 軸方向で内向き)ですから、隠線処理が簡単になって、輪郭線を
tan(αn) = -emx/dmxとして求めることができます。X-Y 平面なら、
enz < 0 陽線 enz = 0 輪郭線 enz < 0 隠線 tan(αn) = -emz/dmzです。透視投影だと、はるかに複雑になって、隠線処理もやっかいです。
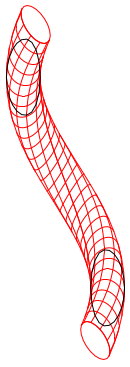
素線の断面形状は、撚合わせの最小ピッチや中心介在の最小径を求めたり、密巻ピッチ を求めるとき必要になります。
表面の座標は撚の中心軸を z 軸として
x = -b*cos(α)*cos(β) + b*cos(φ1)*sin(α)*cos(β) + a*cos(α) y = -b*sin(α)*cos(β) - b*cos(φ1)*cos(α)*sin(β) + a*sin(α) z = b*sin(φ1)*sin(β) + a/sqrt(k2 - 1)*(α - α0) ここに tan(φ1) = sqrt(k2^2 - 1) α0 = 初期位相
z 軸から最も離れた素線表面は β = 2*n*π (n = 0, 1, 2, ..) の螺旋で、
x = b*cos(α) + a*cos(α) y = b*sin(α) + a*sin(α)ですから、
sqrt(x^2 + y^2) = a + bとなって、撚の外径は a + b、つまり、 素線断面の厚さは変化しないことがわかります。
同様に、z 軸に最も近い素線表面は β = (n+1)*π (n = 0, 1, 2, ..) の螺旋で、
x = -b*cos(α) + a*cos(α) y = -b*sin(α) + a*sin(α)ですから、
sqrt(x^2 + y^2) = a - bになります。
s2 曲面の z = z1 断面は
α = b/a*(sin(φ1)^2/cos(φ1)*sin(β) + z1/a*(√(k1^2 - 1) + α0s2 曲面の x = 0 断面は
α = atan((b*cos(β) - a) / (b*cos(φ1)*sin(β)))s2 曲面の y = 0 断面は
α = atan((b*cos(φ1)*sin(β)) / (a - b*cos(β)))
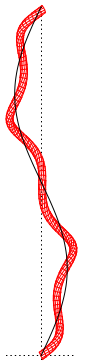
図4の黒線は x = 0 または y = 0 断面です。
ピッチが等しく半径の異なる2つの素線が隙間なく隣接する場合は、位相がα0だけず れている2つの s2 曲面のケーブル中心までの距離を a1, a2、 素線半径を b1, b2 と すれば、隣接条件は
(b1 + b2)^2 = a1^2 + a2^2 - 2*a1*a2*cos(ψ) + (a2*√(k1^2 - 1)*sin(ψ))^2 sin(ψ) = a1/a2/(k1^2 - 1)*(α0 - ψ) ここに、 ψ = α2 - α1となることが証明できて、第2式からψを求め、それを第1式に代入すれば、a1, a2, b1 から b2 を求めることができますが、 第2式からψを陽に解く方法がないため、 2分法などの数値解法を使うことになります。 ψがわかれば、第1式から k1 が得られて、撚ピッチとα2(次の導体の位置)が わかります。
現実のケーブルでよく見られる、ピッチが等しく同じ半径の N 本の素線が隙間なく隣接 する場合は、隣接素線の位相差が α0 = 2*π/N になりますから、a = a1 = a2, b = b1 = b2 として、
b/a = √(1 + (cos(ψ)*√(k1^2 - 1))^2)*sin(ψ) sin(2*ψ) = 2/(k1^2 - 1)*(π/N - ψ) ここに N = 撚素線数 b = 素線半径 k = 素線の撚込係数 a = 撚の内接円半径この場合も数値的に解くしかありませんが、これが同一径の素線を使う同心撚の最小コ ア径ないしは最小撚ピッチになります。Z 軸断面はかなり歪みますが、外径は変化しな いことに注意してください。 N == 1 ならドラム巻きの密巻条件になります。
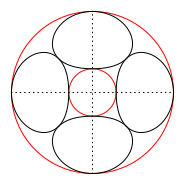
異なる半径の素線を同じピッチで撚合わせる場合は、 隣接導体間の α0 の合計が 2*π になるような撚ピッチを求めることになりますが、 この場合も前記の式を変形した、
(2*π*a1*a2/p)^2*cos(ψ)^2 + 2*a1*a1*cos(ψ) + (b1+b2)^2 - a1^2 - a2^2 - (2*π*a1*a2/p)^2*cos(ψ)^2 = 0 α0 = (2*π/p)^2*a1*a2*sin(ψ) + ψを使って、撚ピッチ p を2分法などの数値解法で求めることができます。
整列巻でケーブルを密巻するときの巻き付けピッチは、 前記のピッチが等しく同じ半径の N 本の素線が隙間なく隣接する場合の式で N = 1 にした
b/a = √(1 + (cos(ψ)*√(k1^2 - 1))^2)*sin(ψ) sin(2*ψ) = 2/(k1^2 - 1)*(π - ψ)から k1 を消去した
(b/a/sin(ψ))^2 = 1 + (cos(ψ))^2*2*(π- ψ)/sin(2*ψ)から ψ を求め、その後
k = sqrt(1 + 2*(π- ψ)/sin(2*ψ)) p = π*(a + b)/sqrt(k^2 - 1)から巻き付けピッチが得られますが、解析的には解けませんから、 2分法などの数値計算を使うことになります。
1 << b/a の場合は、楕円近似を使って
p*sin(φ1) = 2*b cos(φ1) = 1/k1 (k1*p)^2 = p^2 + (π*(a+b))^2から
p = 2*b/√(1 - (2*b/π/(a+b)^2) ∼ 2*b*(1 + (1/2)*(2*b/π/a)^2) (b << a)となりますが、この場合は撚込係数が大きいため、 素線の捻れを考慮しても、 密巻ピッチはほとんど変わりません。 例えば、胴径 160 mm ドラムに 25 mm 径のケーブルを密巻すると、 密巻ピッチは 25.023 mm になります。
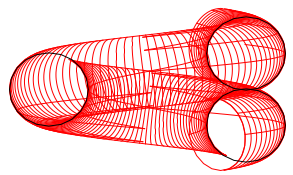
撚線導体を使った対撚の減衰が同じ導体と絶縁体であるにもかかわらず、普通撚 (ordinaly lay)に比べてラング撚(Lang's lay)のほうが少ないのですが、 対撚導体の素線中心は c2 曲線ですから、その素線とケーブル中心線の撚角を考 えると、この理由がわかります。
すぐ後で述べるように、c2 曲線と z 軸の角度の変化分はφ2だけで決まるため、
φ2 = atan((√(k2^2 - 1) + b/a*cos(φ1)*sin(φ1)) / (1 - b/a*sin(φ1)*cos(β))でβに対するφ2の変化を考えると、
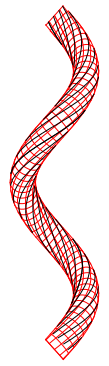
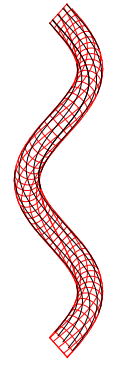
赤色の管状(s2)曲面は 右上から左下に進む(Z)側面が外側(手前)、左上から右下に進む (S))側面が内側(奥側)になり、黒色の(c2)曲線は、左が普通撚、右がラング撚ですが、 曲率線(赤線)と比べると、ラング撚は内側で Z 軸との角度が小さく外側で大きくなる ことがわかります。
この図や t2 の式から見抜くのは無理ですが、黒線の接線ベクトルと Z 軸の角度を計 算してみると、黒線と Z 軸の角度はαに関係なくβだけで決まることがわかります。
1 次素線と 2 次曲線の曲率(curvature)と捻率(tortion)は下記のようになります。
κ1 = sin(φ1)^2/a
= (k^2 - 1) / (a * k^2)
τ1 = cos(φ1)*sin(φ1)/a
= √(k^2 - 1) / (a * k^2)
κ2 = √(κe2^2 + κg2^2)
τ2 = cos(φ2)*sin(φ2)/b/h2
ここに、
a = 1 次素線の半径
κ1 = 1 次素線の曲率
τ1 = 1 次素線の捻率
κ2 = 2 次素線の曲率
τ2 = 2 次素線の捻率
κe2 = (1 - cos(φ2)^2/h2)
κg2 = κ1/h2*cos(φ2)*sin(β)*(1 + sin(φ2)*μ2
h2 = 1 - κ1*b*cos(β)
μ2 = sin(φ2) - b*τ1*cos(φ2)/h2
1 次素線は常螺旋ですから曲率と捻率が一定で簡単ですが、2 次以上の素線については
曲率も捻率も場所によって変わりますから、かなりやっかいです。
この捻れ問題でよく遭遇する事例としては、コイル(束)状に巻かれた電線や紐を コイルの中心から上に引き出す場合で、 コイルに巻かれた状態では k = ∞、素線の曲率は 1/コイルの半径、 捻率は 0 ですが、素線をコイルが置かれた平面から離して、 上に引き上げると k は有限の値になって 1 に近付いてゆき、 直線状になった時点で k = 0、曲率 0、捻率 2*π、 つまり、1 巻き分について 1 回転の捻れを生ずることになります。 この捻れを防ぐにはコイルを素線 1 巻に対して 1 回転づつ回転させるしかありません。
また、 撚機の素線供給ボビン(ドラム)枠の自転はτ1で決まりますが、 1 ピッチの素線長は 2*π*a/sin(φ1) ですから、素線 1 ピッチあたりの捻れは
τ1*2*π*a/sin(φ1) = 2*π*cos(φ1) = 2*π/k1となって、k1 〜 1 なら 1 回転(2*π)になります。通常の撚機は 1 ピッチあたり 1 回の自転で設計されていますから、 撚あがったケーブルの素線には撚が締まる方向の捻れ が付加されることになります。多くの場合、これは撚構造を安定化させる利点がありま すが、k1 が大きな密撚の場合は撚加工中にキンクを生じて、撚加工を不可能にすること があります。
なお、常螺旋の場合は曲率と捻率の比 κ/τ が一定で、 撚ピッチを変化させると曲率と捻率は同じ割合で増減します。 コイルからの素線引き出しは、この関係が極端に表面化するケースです。
ケーブルを円形の棒に巻き付ける場合は、ケーブルの中心線が円になりますから、前記 の c0 曲線を円にして、順次計算してゆくことになりますが、計算の手間が少し増えま す。
折り曲げ試験で重要な、1 次素線の曲率と捻率を計算すると、下記のようになりま す。
κ1 = √(κe1^2 + κg1^2) τ1 = cos(φ1)*sin(φ1)/a/h1 ここに、 κ1 = 1 次素線の曲率 τ1 = 1 次素線の捻率 κe1 = (1 - cos(φ1)^2/h1)/a κg1 = κ0/h1*cos(φ1)*sin(α)*(1 + sin(φ1) h1 = 1 - κ0*a*cos(α) κ0 = ケーブル中心線の曲率
この解説とはパラメータの選択が少し違いますが、 下記の文献が一番だと思います。
小野進,- ワイヤロープの微分幾何学的考察 (日本応用数学会論文誌) Vol.3, No. 4, 1993, pp.387-424著者は東京製綱株式会社の社長業の合間にこの研究を進めたということで、ほぼ同じ内 容が「ワイヤロープハンドブック」(日刊工業新聞社 ISBN4-526-03673-0)にも収録され ています。この論文で使われているパラメータ An は、 撚ピッチを pn として An = pn/(2*π*an)、 つまりピッチ円の周長で規格化したピッチであることに気づくと、 理解しやすいと思います。
世界的に見ても、撚込係数(撚の角度)について対極にある、 ワイヤロープとバネの両分野で、 長年にわたり不完全な解析に終止していて、 ようやく部分的に微分幾何学を採り入れたのが、
Lee.W.K,- AN INSIGHT INTO WIRE ROPE GEOMETRY (Int. J. Solid Structures, 28(1991), pp 471-490のようで、組織的計算が可能になったのが小野論文と思われますから、 人類が巻き付けや撚構造に於ける微分幾何学的解析の重要性に気づいたのはかなり最近 だったことがわかります。
私自身が最初に微分幾何学的解析の重要性に気づいたのは、1963 年の学生時代で、 電線製造下請企業の経営に参加した父の防衛庁向け撚加工の下請仕事で、 ピッチが極端に小さい撚加工がうまくゆかないから見てくれという要請でした。 そこで始めて、空間曲線の捻れを真剣に考えざるを得なくなったのですが、 その少し前に購入した、スミルノフの大著「高等数学教程」のおかげで、 初歩的な微分幾何学の手法がわかって、 常螺旋の捻率が撚込係数で簡単に表現できることに気づき、 引き受けた撚加工を完成させることができました。私の父は、 このことを死の直前まで覚えていて、私の妻に話したそうです。 この本は学生時代に昼食抜きでお金を貯めて神田の書泉で購入したのですが、 学生が大著を買ったので書店主が同情して値引きしてくれました。 独禁法で守られている書籍を値引きしてもらったのは、後にも先にも、 このときだけです。これを自宅に持ち帰るとき、その一部を読むの に夢中になって、自宅のある豪徳寺駅で小田急線から下車したとき、 残りを電車の網棚に置き忘れ、小田原まで遺失物を引き取りに行きました。
当時は自分が父の後を継ぐとは思わなかったのですが、父とその友人の大失敗で、 後始末を引き受けざるをえなくなって、その会社を再建し、いろいろな場面で、 何度も微分幾何学が必要になって、前記の論文とは関係なく、 いろいろな解析をしてきました。基本的なパラメータを撚込係数にしたのは、 電線の製造現場では撚込係数が最も基本的で扱い易く、応用しやすいためです。 ただ、撚込係数だと撚方向 S よりと Z よりの区別ができないのが欠点で、 汎用性を重視する場合は、より角 atan(sqrt(k^2 - 1)) かピッチ角 atan(1/sqrt(k^2 -1)) を使うほうが良いと思います。
この解説の分量では説明しきれない本来の微分幾何学そのもの の本はたくさんありますが、 コンピュータプログラミングの(曲線と曲面)図形処理を扱った書籍も 参考になると思います。
管状曲面とその上の曲線について、3 次までの Fn, hn を計算した結果は次のようにな ります。
h1 = 1 h2 = 1 - b*κ1*cos(β) h3 = 1 - c*κ2*cos(γσ2) F1 = 0 F2 = b*τ1 F3 = c*τ2 κ1 = sin(φ1)^2/a κ2 = √(τge^2 + τg2^2) κe2 = (1 - cos(φ2)^2/h2)/b κg2 = κ1/h2*cos(φ2)*sin(β)*(1 + sin(φ2)*μ2) τ1 = cos(φ1)*sin(φ1)/a τ2 = cos(φ2)*sin(φ2)/b/h2 τ3 = cos(φ3)*sin(φ3)/c/h3 μ2 = sin(φ2) - b*τ1*cos(φ2)/h2 φ1 = atan(√(k1^2 - 1) φ2 = atan((√(k2^2 - 1) + F2)/h2) φ3 = atan((&radicr(k2^3 - 1) + F3)/h3) ここに、 κn = n 次の曲線の曲率 κen = n 次の曲線の法曲率 κgn = n 次の曲線の測地的曲率 τn = 次の曲線の捩率 μn = n 次の曲線のαn/(αnまでの素線長)
ここでは、gnuplot の作図データを awk で作成していますが、 私自身は遥か昔に自作した plt と呼ぶ 数値計算と作図の機能を持つプログラミング言語を使っていました。 コメントの漢字コードは EUC-JP です。
図1 s1.txt 図2 s2.txt, s3.txt 図3 s4.txt, s5.txt 図4 s6.txt 図5 s7.txt 図6 s8.txt 図7 s9.txt, s10.txt