伝送線路のステップレスポンス

図１ - 特性インピーダンスで終端された伝送回路

特性インピーダンスで終端された伝送回路の入力電圧と出力電圧の関係が下記のように、 伝搬定数 γ と伝送線路の長さ l で表現できることは、よく知られています。

  E2/E1 = exp(-γ*l)                                       (1)
  ここに、
	E1 = 入力電圧 (V)
	E2 = 出力電圧 (V)
	l = 線路の長さ (m)
	γ = 伝搬定数
	   = sqrt((R + j*ω*L)*(G + j*ω*C))
	R = 線路の導体抵抗 (Ohm/m)
	L = 線路のインダクタンス (H/m)
	G = 線路のコンダクタンス (S/m)
	C = 線路のキャパシタンス (F/m)
	ω = 2*π*f .. 角周波数
	f = 周波数 (Hz)
	π = 3.14159165..

  G = ω * C * D
  ここに、
	D = 誘電体の損失率 (tanδ)
	  = (1 cycle 毎に失われるエネルギ) / (C に蓄積されるエネルギ)

導体抵抗 R は導体の表皮効果などの渦電流損失が原因で、 高周波では、ほぼ周波数の平方根に比例して増加し、 これがケーブルの減衰のほとんどを占めます。

キャパシタンス C とインダクタンス L の周波数依存性は究めて小さく、 通常は一定と考えてよいのですが、 パルス伝送の場合は、導体の渦電流による、ごく僅かな L の周波数特性が、 伝送波形に大きな影響を与えます。

さて、E1 が正弦波の場合は、

  γ = α + j*β
  ここに、
	α = 減衰定数 (neper/m)
	β = 位相定数 (rad/m)

  E2 / E1 = exp(-α*l)*exp(-β*l)

一般に、ケーブルの減衰は導体径に反比例して増加し、 周波数の平方根に比例して増加しますから、 導体が細いほど、また、 周波数が高いほど出力電圧は低下するわけで、 いずれにしても、 減衰が増えれば出力電圧が減小します。

一方、 E1 がパルス波形の場合は、周波数特性の代わりに、 時間軸のステップ応答を考える(注２)ことになりますが、 例えば、 同じ長さで減衰の異なるいくつかの同軸ケーブルのステップ応答を求めると、 次ぎのようになります。

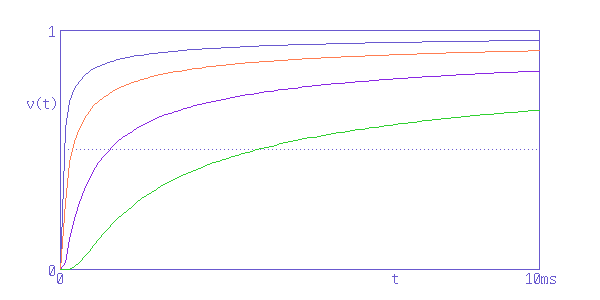
図２ - 同じ長さで減衰の異なるいくつかの同軸ケーブルのステップ応答

これらは、いずれも G = 0 の良質な高周波ケーブルの特性で、 オシロスコープで観測した波形とも一致しますが、 一番上が最も減衰の少ないケーブルで、これを基準に、 その下が２倍、その下が４倍、一番下が８倍の減衰になっています。

これを見ると、正弦波と同じように、ステップレスポンスでも、 減衰の大きなケーブルは出力電圧が低下しています。

では、時間が無限に経過した場合、 ステップ応答の出力電圧はどうなるのでしょうか？　

これが、今回の問題です。

平林 浩一, (C) 2008

注１ - ケーブルの位相定数と速度係数

位相定数は

  位相定数 = 2*π*f/vp
  ここに、
	vp = 位相速度 (m/s)

注２ - ケーブルのステップ応答

一般の高周波ケーブルでは、

  G << j*ω*C

  E2/E1 = exp(-l*sqrt((R + j*ω*L)*j*ω*C))                        (2)

E1 がステップ入力(Heaviside の Unit function)

  E1 = 1   (0 <= t)
     = 0   (t < 0)

  E2/E1 = exp(-R/2/L*t)*I0(R/2/L*sqrt(t^2 - L*C*l^2))  (sqrt(L*C)*l <= t)
	= 0  (t < sqrt(L*C)*l)
  ここに、
	I0(x) = 0 次の変形ベッセル関数

しかし、現実のケーブルでは導体の表皮効果などの渦電流損失による R の周波数特性と、 L のうち位相歪の原因となる内部インダクタンス (導体内部の磁束に起因するインダクタンス) の周波数特性が大きいため、 この解析解は現実と似てはいますが、明瞭な違いがあります。