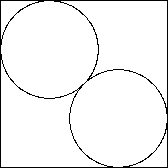
2 - sqrt(2)
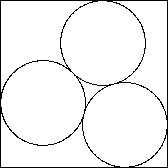
4 / (4 + sqrt(6) + sqrt(2))
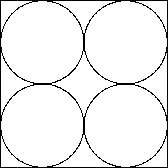
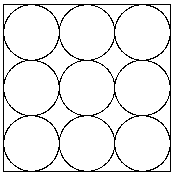
1/2
sqrt(2) - 1
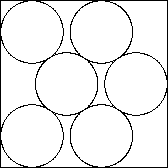
(6 * sqrt(13) - 13) / 23
2 / (4 + sqrt(3))

sqrt(2) / (1 + sqr(2) + sqrt(3))
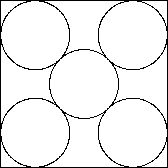
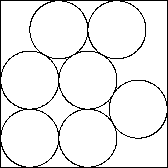
1/3
日頃頻繁に遭遇する問題であるにもかかわらず、 簡単に解が得られないという状況は多いのですが、 例えば、パレットに電線ドラムを平積みするときに問題になる、 同じ大きさの円 n 個を単位正方形に詰め込むとき、 円の直径の最大値と中心配置がどうなるかという問題もその 1 つで、 幾何学に於ける未解決問題の 1 つになっています。
とは言え、日常必要になる簡単な場合だけでも解は必要ですし、 プログラムを考えること自体も楽しいですから、 ある程度は役にたつプログラムを考えてみましょう。
コンピュータで解く場合は、単位正方形を離散化し、 どの場所に円の中心を置けばよいかをシラミ潰しに探索することになりますが、 まず、問題を変形して、 n 個の点を単位正方形内に配置し、 2 点間の距離の最小値が最大になる配置を求めることにすれば、 円のはみ出しを考慮する手間が減って、取扱が少し楽になります。
この問題で得られた2 点間の距離の最小値の最大値を d とすれば、 直径 d の円を 1 辺の長さが 1 + d の正方形の中に詰め込めることになります。
次に、単位正方形を (M - 1) * (M - 1) 個の小さな正方形に分割し、 個々の正方形の 4 隅、つまり格子点に n 個の点を配置することにしますが、 プログラムの多重ループを避けるため、 格子点に下記のような通し番号を割り当てて、 2 次元座標を1 次元化します。
(N-1)*N . . . . N*N-1
. . . . . .
2*N 2*N+1 2*N+2 . . 3*N-1
N N+1 N+2 . . 2*N-1
0 1 2 . . N-1
この 1 次元座標 i = (0, 1, .. N*N-1) と元の 2 次元座標の格子点 (x, y) の位置関係は次のようになります。
x = (i % N) * ds (0 <= x <= 1) y = (i / N) * ds (0 <= y <= 1) ds = 1 / (N - 1) (ds < 1)ds は格子間隔です。
この結果前記の問題は、
というMinMax 問題のすっきりした プログラムになります。
さらに、 組み合わせの生成に繰り返しループを使わず再帰手続きを 使うようにすれば、 M や n に依存するループ処理のない汎用プログラムを書くことができます。
この方針で smin を何回計算することになるかというと、
combination(N*N, n) * combination(n, 2) = (N*N)! / (n! * (N*N - n)!) * n! / (2! * (n - 2)! ここに、 n <= N*N combination(n, r) = n! / (r! * (n - r)! = n 個から r 個とる組み合わせの数ですから、実際に計算して見るとわかりますが、わずかに N が増えるだけで、 計算量が爆発的に増え、たちまち宇宙の年齢を越えても計算が終らなくなります。
計算不能にならないためには N を小さくしなければなりませんが、 最も簡単な n = 2, 4, 9, 16, .. (自乗数) のケースなら sqrt(n) <= N の分割で済みます。 ところが、これ以外のケースになると、もっと細かな分割が必要で、 n = 8 になると、11 <= N の分割、つまり、 計算しなければならない組み合わせは 400 億あるいはそれ以上になります。 これは、お茶でも飲んでいれば終るといった計算量ではありません。
ただ、実用的な誤差 2, 3 % を許すことにすれば、 正しい配置にはならないものの、比較的少ない分割で済みます。 (注1)
このあたりの感覚を手軽に得るために、 上記の方針で作ったプログラムの1例を付けておきます。
前記の方法では (格子点間隔 / 2) の誤差は避けられませんが、 得られた配置形状(位相幾何学的位置関係)が 正しいものであれば、 その格子点の周辺に正しい座標があるはずで、 格子点間隔の 1/2 の距離で探索を続ければ精度を高めることができます。
この精度の改良に2 分法を使うことにすれば、 前記計算で得られた格子点を中心に、 それまでの格子点間隔の 1/2 離れた 8 つの隣接点について、 2 点間距離の最小値の最大値を求めればよくて、 この計算量は
combination(9, 2) * nですから、格子点間隔を 1/2 にして前記の計算を行う場合と比べれば、 大幅に減少します。
この計算は前記の 1 次元座標を
新しい 1 次元座標 = (i % N) * 2 + (i / N) * 4 * N 新しい N = N * 2 新しい ds = ds / 2と変換して、前記の方法で計算することもできますが、 今度は「はみ出し」の検査も必要ですし、 通常のデカルト座標 (x, y) [0<=x, <= 1, 0<=y<=1] を使い、 新しい ds が 0.01 を切ったらやめるといった方法のほうがよいと思います。 (注2)
2 から 9 個までに対する最終的な結果は次のようになります。 配置図の下の値は円の直径ですが、これは上記の 計算から得られた配置に対する幾何学的計算から求めました。 直観的にはわからない配置があります。 (注3)
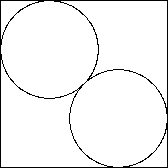
2 - sqrt(2) |
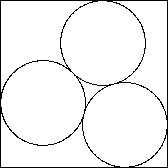
4 / (4 + sqrt(6) + sqrt(2)) |
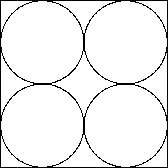
1/2 |

sqrt(2) - 1 |

(6 * sqrt(13) - 13) / 23 |

2 / (4 + sqrt(3)) |

sqrt(2) / (1 + sqr(2) + sqrt(3)) |

1/3 |
この問題に本気で取り組みたくなった場合は、手をつける前に、 せめて下記程度は見ておくと無駄に時間を捨てずに済むと思います。
H.T.クロフト・K.J.ファリコナー・R.K.ガイ,- 幾何学における未解決問題 (シュプリンガー・フェアラーク東京) ISBN4-431-70677-1
さらに深く知りたいかたは
P.G.SZABO, M.Cs.MARKOT, T.CSENDES, L.G.CASADO, I.GARCIA,- NEW APPROACHES TO CIRCLE PACKING IN A SQUARA, Springer, 2007 ISBN 0-387-45673-2がすばらしいです。
最近の結果については著者の 1 人による http://www.packomania.com/。
正方形でなく円への詰め込みについては http://hydra.nat.uni-magdeburg.de/packing/cci/
誤差 2 % 程度でよければ、この方法でも、たいした時間は要りませんが、 近似計算であれば、他にもいくつか方法があります。
例えば、最初に乱数などで単位正方形内に n 個の点を選び、Voronoi 分割します。 次に、Voronoi 領域の母点を個々の Voronoi 領域の重心に移動し、 再度 Voronoi 分割するという操作を母点の移動量が十分小さくなるまで、 繰り返します。 その後、母点間距離の最小値が最大になる場所を連続あるいは離散 MinMax 法で 計算します。
こういった方法で得られる解は乱数などで決める初期配置に依存しますので、 運任せにはなりますが、比較的少ない計算量で適当な精度の解が得られます。 もちろん、正しい配置が得られるという期待は持てません。
さらに高度な手法については前記の文献(ISBN 0-387-45673-2)を見てください。 物理的なシミュレーションとかいろいろなアプローチが記述されています。
格子間隔 1/2 の隣接点から始める以外に、 2/3 離れたところから始めるなど、 局所最適化の開始点を変えると、 比較的少ない計算量で正しい配置が得られる場合がありますが、 これも正しい結果を知った後でわかる後知恵になります。
前記のプログラムでは単位正方形を正方形で分割しましたが、 三角形で分割すると、 もう少し少ない計算量で済むようです。
kh@mogami-wire.co.jp, 2012-02-13, 2012-03-15