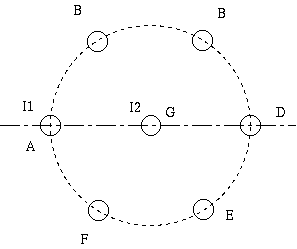
Carson の平行往復導体の解析の実用的別解を見出した Dweight は 送電線などで使われる導体群(group of conductors)の解析に取り組み
H.B.Dwight,- Proximity Effect in Group of Round wires Gen. El. Rev., p531-536, November 1927を発表しました。 (注1)
この論文では、複数の素線から構成される導体群の交流抵抗を求めるわけですから、 個々の素線の表皮効果に加えて、 相互インダクタンス(mutual inductance)と近接効果(proximity efect)を考慮することになって、 かなり複雑な計算になりますが、 送電線でよく使われる 4 導体正方形配置と単線の三相導体について、 平行配置、正三角形配置について、 Rac/Rdc を計算しています。
単線導体と比べて導体群の解析が面倒なのは、 同じ相でも導体群を構成する個々の素線の電流が異なるためで、 まず、同一地点(距離)で見ればすべての導体の電位差が 0 になることを利用して、 個々の導体の電流比を求め、 全電流を個々の導体に配分してから、 個々の導体で発生するJoule熱をPoyntingベクタから求め、 その合計値から導体群の交流抵抗を求めるという方針です。
ここまでくると、 日常良くみかける7芯導体の解析は応用問題の枠内になりますが、 この課題は J.E.L.Tweedalle が
J.E.L.Tweeddale,- Proximiy Effect in a Seven-Strand Cable Trans. Am. I.E.E. 46, P1148-1152, 1927で解きました。
これは Dwight の結果を素直に7芯導体に適用したもので、 目新しいことはないのですが、日常よく見られる典型的撚線導体ですから、 ここでは、Tweeddale の7芯導体の計算を Rac/Rdc から Zac/Rdc に拡張したプログラムで、導体群特有の性質を解説します。
交流抵抗については、 密接配置の7芯導体を含めて、 円形撚線の Rac/Rdc は同じ導体断面積の単線導体の表皮効果とほとんど変わらないのですが、 結果を生む原因については回路的に大きな違いがあって、 単線の場合は表皮効果、 導体群の場合は相互インダクタンスが主役になります。

1図 7芯導体
J.E.L.Tweeddale による計算手順は次ぎのとおりです。 (注2)
W1 = (b/2)*(I1*conj(I1)/(π*a*a*σ)*0.5*b*j*sqrt(j)*J0/J1)
∞
+ (b/(π*w*σ*σ)*Σ(Mn*conj(Mn)*UV(n))
m=1
W2 = (b/2)*(I2*conj(I2)/(π*a*a*σ)*UV(0))
∞
+ (b/(π*w*σ*σ)*Σ(Nn*conj(Nn)*UV(n))
m=1
A0 = j*α*a/(2*J1)
An = I2/(π*a*a)*(a/s)^n*j*α*a/Jn-1
+ I1/(π*a*a)*(a/s)^n*j**α*a/Jn-1*(2*cos(n*π/3
+ 2/sqrt(3)^n*cosn*π/6) + 1/2^n)
∞
Bn = Σ*(a/s)^(m+n)*Jm-1/Jn-1*(n+m-1)!/(n-1)!/m! * (Fm*cos(m*π)
m=1
+ *2*Am*cos(π(m-n)/3) + 2*Am/sqrt(3)^(m+n)*cos(π*(m-n)/6)
+ Am/2^(m+n)
Cn = Bn で A を B、F を G に置き換えたもの、以下、同様
Fn = I1/(π*a*a)*(a/s)^n*j**α*a/Jn-1*(cos(n*π) + 2*cos(2*n*π/3)
+ 2*cos(n*π/3) + 1)
∞
Gn = Σ(*Am*(a/s)^(m+n)*Jm+1/Jn-1*(n+m-1)!/(n-1)!/m! * (cos(n*π)
m=1
+ 2*cos(2*n*π/3) + 2*cos(n*π/3) + 1))
Hn = Gn で A を B に置き換えたもの、以下、同様
Mn = An + Bn + Cn + ..
Nn = Fn + Gn + Hn + ..
UV(n) = 0.25*b/(w*U2*σ*σ)*Jn(n,j*α*a)
*j*sqrt(j)*conj(Jn(n,j*α*a))
ここに、
Zac = 往復平行線路のインピーダンス (Ω)
Rdc = 往復平行線路の直流抵抗 (Ω)
= 1/(π*a^2*σ)
J0, J1, J2, .. Jn は j*α*a を引数とするBessel関数
Jn' = (d/dx)Jn(x) .. Jn の微分
α = sqrt(j*ω*μ*σ)
b = a*sqrt(ω*μ*σ)
j = sqrt(-1)
ω = 角周波数 (rad)
= 2*π*f
f = 周波数 (Hz)
μ = 透磁率 (H/m)
σ = 導電率 (siemens/m)
a = 導体半径 (m)
s = 中心導体と外周導体の中心間距離 (m) (2*a <= s)
conj(z) = 複素数 z の共役複素数
W1 = 外周導体(A,B,C,D,E,F)の内部エネルギ (joule/m^2/s)
W2 = 内部導体(G)のインピーダンス(&Ohm;) (joule/m^2/s)
I1 = 外周導体(A,B,C,D,E,F)の全電流 (A)
I2 = 内部導体(G)の全電流 (A)
U2 は後述
かなり面倒ですが、
W1, W2 は各素線外周から導体内部に侵入する電磁エネルギを
複素Poyntingベクタで求めた値で、
その実数部がJoule熱iとして消費されるエネルギ、
虚部が蓄積される磁気エネルギ(magnetic energy)になります。
W1 と W2 の第 1 項は素線導体の表皮効果、 残りの項が他の導体に流れる電流の近接効果になります。 あちこちに出て来る無限級数は電流の一部を無限級数で解いて積分可能にし、 その積分を実行した結果です。
W1, W2 には未知の電流 I1, I2 が含まれますが、 これは導体群の軸に直交した面では 全素線(A,B,C,D,E,F,G)の電位が等しいことを利用して、 各素線の単位長あたり電圧降下 Ea, Eg を求め、 Ea = Eg から k = I2/I1 の比を求め、 導体群全体の電流を I (A) とすれば
I = I1 + 6 * I2から、
I1 = I / (6.0 + k) I2 = I * k / (6.0 + k)で決定することができます。 ここで、I = 1 とすれば、 W1, W2 は導体の内部インピーダンスになることに注意してください。
Ea, Eg は次ぎのようになります。
Ea = I1/(π*a*a*σ)*A0*J0 + j*U*ω*2*log(1/s)
+ j*U*ω*2*log(1/(6*a*s^5)
∞
+ j*U2*ω*2*Σ(Nn*π*a*a*cos*(n*π)(a/s)^n/n*Jn+1/(j*α*a)
n=1
∞
+ j*U2*ω2*πa*a*Σ(Mn*Jn+1/(j*α*a)*((a/s)^n/n
n=1
* (2*cos((n*π/3) + 2/sqrt(3)^n*cos(n*π/6) + 1/2^n)
Eg = I2/(π*a*a*σ)*A0*J0 + j*U*ω*2*log(1/a)
+ j*U*ω*12*log(1/s)
∞
+ j*U2*ω12*πa*a*Σ(Mn*Jn+1/(j*α*a)*(a/s)^n/n)
n=1
U = μ0/(4*PI)
U2 = 4*PI*ε0
μ0 = 4e-7*π .. 真空の透磁率 (H/m)
ε0 = 4e7*π/(4*π*c*c) .. 真空の誘電率 (F/m)
c = 2.99792458e8 .. 真空中の光速 (m/s)
ここに、
Ea = 外周導体の単位長あたり電圧降下 (V/m)
Eg = 中心導体の単位長あたり電圧降下 (V/m)
Ea, Eg の第 1 項は素線導体自体の表皮効果、 log() を含む項は他の導体からの相互インダクタンス(mutual inductance)、 残りの項が他の導体の電流による近接効果です。
Ea の第 3 項は導体 A から導体 B, C, D, E, F 間の相互インダクタンスの対数項 を加算した結果です。 (注3)
log(1/a)+2*log(1/s)+2*log(1/(sqrt(3)*s)+log(1/(2*s)) = log(1/(6*a*s^5)また、
cos(n*π) + 2*cos(2*n*π/3) + 2*cos(n*π/3) + 1)は n % 6 == 0 とき 6、n % 6 != 0 のとき 0 になりますから、 Fn, Gn, Hn, .., Nn は n % 6 != 0 のとき 0 です。
定数 U と U2 は原論文で使われている数式がGauss単位なので、 現代のSI単位に変換するための値です。
Tweeddale の論文の数値計算例は Kennelly と Affel による詳細な実験
A.E.Kennelly, H.A.Affel,- SKIN-EFFECT RESISTANCE MEASUREMENTS OF CONDUCTORS Proc. I.R.A. May, 1917, p523-555に含まれる 22 AWG 7 芯導体群で、 a = 0.644e-3 (mm)、s = 1.00*d, 1.05*d, 1.88*d, 3.85*d, 6.32*d, 9.98*d についての実測データの僅か 2 点ですが、 このプログラム例でもこれらの実測結果(Rac/Rdc)との比較ができるように、 同じ値を使いました。
22 AWG 7 芯導体群密接配置(a = 0.644e-3 mm, s/a = 2.00) の Zac/Rdc を計算した結果です。
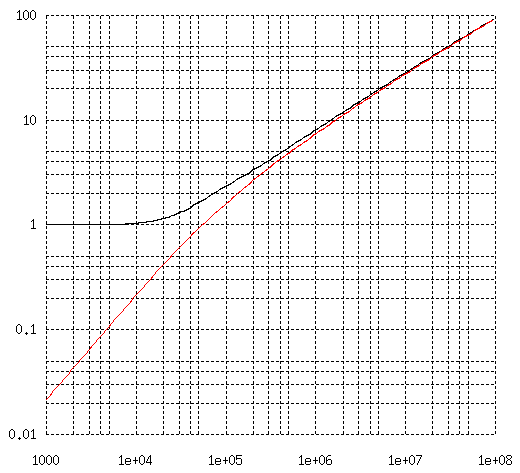
2図 22 AWG 7 芯導体群密接配置の Zac/Rdc
横軸は周波数(Hz)、縦軸は Zac/Rdc、 黒線が実部(抵抗)と赤線が虚部(リアクタンス)です。
Zac の虚部を ωで割れば導体内部インダクタンスが得られます。
Li = Im(Zac) / ω ここに、 Li = 導体内部インダクタンス (H/m) Im(z) = 複素数 z の虚部 ω = 各周波数 (rad) = 2*π*f f = 周波数 (Hz)
例えば、上記の例なら次ぎのようになります。
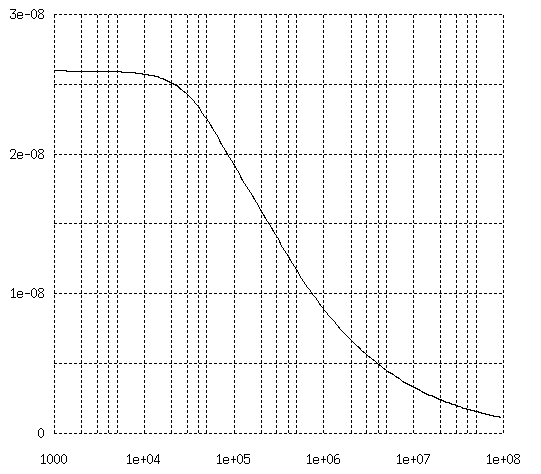
3図 22 AWG 7 芯導体群密接配置の内部インダクタンス
横軸は周波数(Hz)、縦軸は内部インダクタンス(H/m)です。
22 AWG 7 芯導体群密接配置の 100 kHz に於ける 導体外周の電流密度の計算例です。
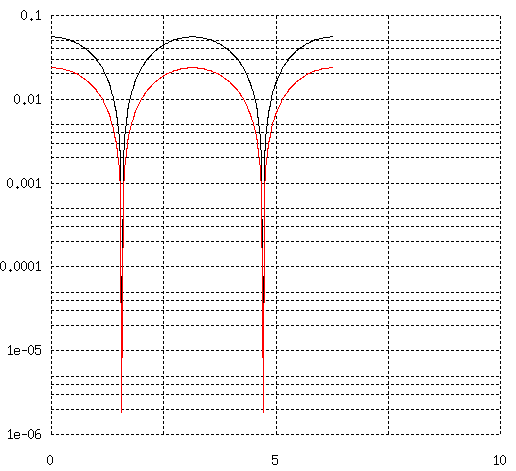
3図 22 AWG 7 芯導体群密接配置の導体外周面電流密度
横軸は偏角(rad)、縦軸が電流密度(A/m^2)で、 黒線は外周導体、赤線は内部導体になります。 渦電流は導体中心を通る面に対象に流れる循環電流ですから、 対象面では 0 になります。
22 AWG 7 芯導体群密接配置の外周導体と内部導体の電流配分計算例です。
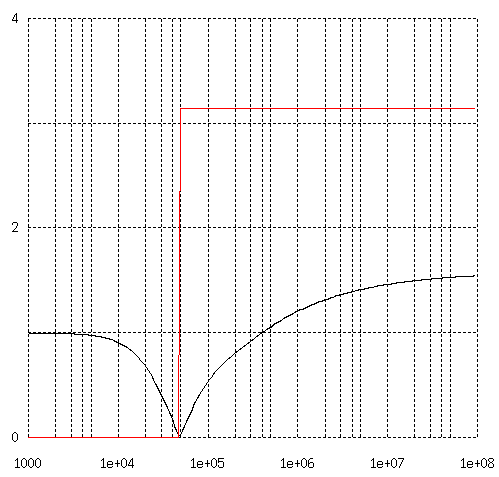
4図 22 AWG 7 芯導体群密接配置の外周導体と内部導体の電流配分
横軸は周波数 (Hz)、縦軸は(内部導体電流/外周導体電流)で、 黒線は絶対値、赤線は位相です。
周波数が低いと 7 本すべての導体に均等に電流が流れますが、 周波数が高くなるにしたがって中心導体の電流が減少し、 まったく流れない周波数があります。 しかし、さらに周波数が高くなると、 内部導体の電流は増加し、 その向きが外周とは反対向きになります!
高周波の場合は単線内部でも、 表皮効果により場所によって電流の位相が異なり、 逆向きに流れるところがたくさんできますが、 同芯配置の導体群の場合は内部導体全体で見て逆になる ことがある点で単純な表皮効果と異なり、 これは導体素線間の相互インダクタンスの効果が大きいためです。 表皮効果は高周波で周波数の平方根に比例しますが、 相互インダクタンスの影響は周波数に比例するため、 支配的になるわけです。
プログラムは c99 以降の複素数をサポートした c 言語で書いてあって、 動作確認は FreeBSD-8.4 (gcc 4.2.1 + gfortran 4.6.3) と FreeBSD-10.3 (clang 3.4.1 + gfortran 4.8.5) で行っています。
Compile は「make」を実行するだけですが、 プログラムの内容や実行結果の理解には原論文が不可欠で、 この解説は原論文を理解するための障害を少しでも減らすことを目的にしています。
main() 中の comment out された関数を含む内容は次ぎのとおりです。
zac(double f1, double f2) - 往復平行線路のインピーダンス proximity(double f1, double f2) - Rac/Rdc inductance(double f1, double f2) - 7芯導体の内部インダクタンス Idensity(a, s, g, u, f, f, t) - 7芯導体素線の周波数 f,半径 r に於ける電流密度 COMPLEX Idensity(a, s, g, u, f, t) - 1図 P 点の電流密度 i2i1(double f1, double f2) - 中心導体の電流/外周導体(1本)の全流 Solid(f, a, u, g) - 単線導体のインピーダンス double a - 導体半径 (m) double s - 導体間隔 (m) double g - 導電率 (S/m) double g - 導電率 (S/m) double u - 透磁率 (H/m) double f - 周波数 (Hz) double t - 偏角 (rad) f1 は計算する 周波数の下限 f2 は上限です。 近接効果による電流密度は表皮効果に比べt小さいので、 Irt() 関数の i1 += I1 * A0(a, A); i2 += I2 * A0(a, A); を comment out にして、近接効果による電流単独で見るほうがよくわかります。
遠方の発電所から都市部の変電所を繋ぐ超高圧送電線を見ると、 3相送電の3組の送電線は3本でなく、 複数の導体を集めた3組の導体群になっていることに気づきますが、 この理由は導体周囲の電位傾度を減らして、 コロナ放電による損失を減らすためです。
導体系を太くすれば導体周囲の電位傾度は減りますが、 重量とコストが極端に増加しますから、 見掛けの太さを大きくするために、 複数導体を使います。
原論文では交流抵抗と直流の比だけ Rac/Rdc を求めていますが、 ここでは私がインピーダンスを求めるように拡張した結果を示しています。 当時はコンピュータが存在しませんから、 実数計算だけでもたいへんな仕事で、 Kennellyの実験結果との一致確認も僅か 2 点でしかやっていません。
計算の詳細は Tweeddale と Dwight の原論文を見てください。 そこでわかりにくい部分はこのテキストで補足してあります。
こういった計算は幾何学的平均距離(GMD- Geometric Mean Distance)を使うと簡単です。
一平面上の多くの面積 A,B,C,.. と、 それらとドウイツ平面上にある他の一つの面積 N との間の GMD を各々 Ra, Rb,Rc,.. とすれば、 面積(A+B+C,..) と N との間の GMD R は
(A+B+C+..)*log(R) = A*log(Ra) + B*log(Rb) + C*log(Rc) + ..という基本定理と
Mij = μ/(2*π)*(log(2*l/R) - 1)の関係から容易に相互インダクタンスと自己インダクタンスが得られます。
平林 浩一, 2017-07-18