リッツ線(Litz-Wire)に関する誤解が多いようで、 間違った解説が多量に流布されていますので、 出来るだけ解り易い説明を考えてみようと思います。
他の導体から十分離れた単線導体の場合なら インピーダンス(impedance)は表皮効果だけで決まるのですが、 リッツ線の場合は、他の導体から十分離れた状態でも
当然、結構ややこしくて面倒な計算になりますが、 この解説では、これらのメカニズムがどう関係するかの理解が容易な 7 芯導体の場合を考えることにします。
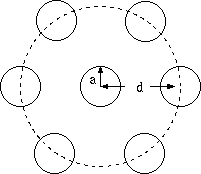
7 芯導体は 1 本の中心素線の周囲に 6 本の素線を密着させた構造で、 機械的に安定した位置関係が保てますので、 電線やロープで最も頻繁に使われる構造です。

1図 - 7 芯導体
リッツ線の場合はこの 7 本の導体素線の間に繊維などのスペーサを入れて、 1図のように少し離した状態にします。 スペーサを必要とする理由については、 後のほうで簡単に触れます。
ここで、a << d、つまり素線径に対して素線間距離を十分離した配置なら、 他の素線との相互インダクタンスと近接効果が無視できますから、 7 芯導体全体としての(並列)インピーダンス(抵抗と自己インダクタンスの合計)が 素線 1 本の 1/7 になることは明らかです。 (注2)
次ぎに d を少しづつ小さくしてゆくと、 今度は素線間の相互インダクタンスが無視できなくなります。 また、周波数が高くなると、 素線の自己インダクタンスと表皮効果が無視できなくなりますが、 これは簡単ですから、同時に考えることにします。 つまり、個々の素線間の近接効果以外を考慮した 7 芯導体のインピーダンスを求めてみましょう。 これだと簡単な交流理論の計算で間に合って、 しかも、導体群のインピーダンス決定メカニズムの理解が容易です。。 (注3)
回路の環路導体は 7 芯導体から遠くに離して、 環路導体とのインダクタンスの素線間の差と 環路導体による近接効果は無視できるような配置にします。 (注4)
この場合は対象性により、 外周導体の電流はすべて同じと見做せますから、 外周導体の1本と内部導体の電流2つがわかれば 7 芯導体全体のインピーダンスが計算できます。
そこで、
Z = 7 芯導体全体としてのインピーダンス (Ω/m)
z1 = 中心素線のインピーダンス (Ω/m)
z2 = 個々の外周素線のインピーダンス (Ω/m)
r = 個々の素線の表皮効果を含めた交流抵抗 (Ω/m)
L1 = 中心素線の自己インダクタンス (H/m)
L2 = 外周素線の自己インダクタンス (H/m)
M0 = 個々の素線と環路導体間の相互インダクタンス (H/m)
M1 = 中心素線と外周の1素線間の相互インダクタンス (H/m)
M2 = 外周の 1 素線と(中心素線を含めた)残りの素線すべてとの間の相互インダクタンス (H/m)
i1 = 中心素線の電流 (A)
i2 = 個々の外周素線の電流 (A)
e1 = 中心導体の長さ方向の電位傾度 (V/m)
e2 = 個々の外周導体の長さ方向の電位傾度 (V/m)
D = 7 芯導体中心から環路導体間までの距離 (m)
ω = 角周波数 (rad/s)
= 2*π*f
π = 円周率 (3.1415..)
f = 周波数 (Hz)
μ0 = 真空の透磁率 (4e-7*π H/m)
j = sqrt(-1)
とすれば、素線の電圧電流関係は
e1 = i1*r + j*i1*L1*ω + j*6*i2*M1*ω - j*6*i2*M0*ω - j*i1*M0*ω (1) e2 = i2*r + j*i2*L2*ω + j*i1*M1*ω + j*5*i2*M2*ω - j*6*i2*M0*ω - j*i1*M0*ω (2)
回路定数のうち、L1, L2, M0 は簡単で、どんな教科書にも書いてあると思いますが、 導体の長さ l について非磁性体なら
L1 = L2 = μ0*l/(2*π)*(log(2*l/a) + 1/4) (4) M1 = μ0*l/(2*π)*(log(2*l/d) - 1) (5) M0 = μ0*l/(2*π)*(log(2*l/D) - 1) (6)
残りの M2 は教科書には書かれていないと思いますが、 応用問題の範囲内で、下記のようになります。(注5)
M2 = μ0*l/(2*π)*(log(2*l/(d*6^(1/5)) - 1) (7)
r については真面目に Bessel 関数で計算しても良いし、 不精すれば Levasseur の近似式でも良いでしょう。
これで、準備ができて、並列接続の集合導体である以上
e1 = e2 (8)ですから
i1*r + J*i1*L1*ω + j*6*i2*M2*ω - j*5*i2*M0*ω - j*i1*M0*ω = i2*r + j*i2*L1*ω + j*i2*M1*ω + j*i2*M2*ω - j*6*i2*M0*ω - j*i1*M0*ω (9)が成立しますので、回路定数を幾何学的パタメータに書き換えて
i2 * (r + j*ω*μ0*(log(2*l/a) + 1/4 + 5*log(2*l/(d*6(1/5))
- 6*log(2*l/d))
= i1 * (r + j*ω*μ0*(log(2*l/a + 1/4) - log(2*l/d)) (10)
これで、外周素線の電流と中心素線の電流比 k が下記のように決まります。
k = (r + j*ω*μ0*(log(d/(6*a)) + 1/4) / (r + j*ω*μ0*(log(d/a) + 1/4) (11)外周素線の電流と中心素線の電流比 k が D の影響を受けないのは、 環路導体が遠くにあるという前提があるためです。
あとは、外周素線と中心素線のインピーダンス z1, z2 を計算し、 それをずべて並列に接続すれば、 集合導体全体としてのインピーダンス Z が得られます。
z1 = r + j*ω*μ0*(log(D^6/(6*d^5*a)) + 1/4 + k*log(D/d)) (12) z2 = r + j*ω*μ0*(log(D/a) + 1/4 + (6/k)*log(D/d)) (13) Z = 1 / (6/z1 + 1/z2)) (14)
(4), (11), (12), (13) 式の 1/4 という項は素線の直流の内部インダクタンスですから、 周波数が高くなると表皮効果により 0 に近付きます。 つまり、正確な計算では表皮効果による L1, L2 の減少を考慮する必要がありますが、 外部インダクタンス(log の項)にくらべてかなり小さいですから、 このまま計算しても大きな影響はありません。 もちろん、近似式を使うとか Bessel 関数による正確な値を使うこともできます。
(13) 式を過去の実測値と比べてみると、 素線間隔 d が素線径の 10 倍以上離れていればほぼ一致した結果が得られます。 (注6)
d がさらに近付くと (14) 式は過小評価になりますが、 これは近接効果を無視したためです。
ここで重要なのは、 撚線導体全体としての表皮効果といったものはないということです。 表皮効果は個々の素線内で発生するもので、 撚線導体全体としては素線間相互インダクタンスが重要な役割を果たします。 (10) 式の k は外周素線に体する内部素線の電流比ですが、 集合導体(導体群)の電気特性の理解には重要で、直流なら 1 ですが、 周波数が高くなるに従って中心素線に流れる電流の位相が遅れることで 導体全体の電流が減り、 さらに周波数が高くなるとマイナスになります。 つまり、高周波では内部素線に逆向きの電流が流れるわけで、 この逆向きの電流が集合導体全体としての電流を減少させます。
また、d が小さくなると中心導体の電流が増加し、 外周導体全体の電流を超えるといったことまで起きます。 よく見られる「集合導体全体としての表皮効果」といったイメージとは 似ても似つきません。
なお、実測したり、近接効果を含む完全な解析を行うと解りますが、 集合導体のインピーダンスは 同じ断面積の単線導体のインピーダンスとほとんど等しくなります。 つまり、 見掛け上素線全体の表皮効果のように見えるわけで、 そそかしい人は集合導体全体としての表皮効果が存在すると思い込みます。 (注7)
しかし、 表皮効果の場合は導体内部に電流が存在しませんが、 集合導体の場合は内側の素線にも電流が流れています。 ただ、その向きが外側の素線の電流の方向と違って、 周波数が高くなると逆向きにさえなるということです。 まったく異なる現象が同じ結果を生むのが不思議ですが、 真の原因はいずれも電磁誘導ですから、同じ結果になるのは自然です。
kの計算は簡単で、導体群の電気特性の理解を深めますから、 不精しないで、やってみてください。自分に対する効率的投資になります。
以上でわかることは、 導体を細かく分割してもインピーダンスは変わらないというこで、 電線にリッツ線を使ってもインピーダンス低減策にはなりません。
AM ラジオのバーアンテナ、中間周波タランスなど、 比較的低い周波数でリッツ線が使われているのは、 コイルにすることで、素線間の相対的位置関係がランダムに変わり、 素線間の相互インダクタンスが均一化されて、 相互インダクタンスの影響を分散するためです。 導体抵抗によるエネルギ損失(発熱)は電流の自乗に比例しますから、 導体群に全電流が同じでも、 素線間の電流の偏りを減らせば、エネルギ損失が減ります。
つまり、リッツ線は表皮効果を減らしているのではなくて、 相互インダクタンスの影響を減らしているのですが、 こういった相互インダクタンスを一様化するための転移(transposition)は 送電路や通信路を含めて、いろいろな場所で使われています。
コイルにしない電線でこれを行うには、 単純な撚線でなく編組(braid)構造を使うのが簡単で、 かなりの改善が得られます。
なお、リッツ線は単に接触を防ぐために絶縁しているわけではなくて、 d/a を最適化するための工夫です。 d/a を大きくすれば高周波抵抗は減りますが、 容積利用率が下がり、直流抵抗が増えてしまいますから、 本末転倒になって、最適値を探すしかないわけです。
インピーダンス(impedance)は エネルギ消費機能としての抵抗(resistance)、 静電エネルギ蓄積機能としてのキャパシタンス(capacitance)、 電磁エネルギ消費機能としてのインダクタンス(inductance)を含んだ概念です。 バネを圧縮すると抵抗を受けるように、 エネルギ蓄積機能には抵抗としての作用もあります。
ここでは表皮効果を抵抗とインダクタンスに分けてしまうことで、 抵抗とインダクタンスに周波数特性を持たせるという代償と引き替えに、 抵抗とインダクタンスの組み合わせという、 簡単な電気回路と解釈できるようにします。
(4), (5), (6) 式のように、 導体間相互インダクタンスは (距離/導体径) の対数に反比例しますから、 かなり離さないと無視できません。 ただ、往復2導体の距離を小さくすれば離れた場所に生ずる磁場が打ち消し合うため、 周囲への影響は激減します。すなわち、 伝送路の往復導体の間隔は出来る限り狭くするのが原則ですが、 架空送電線のように高電圧の線路では放電を避けるため、 かなり幅を広げざるを得ません。
インダクタンスの影響は周波数に比例、 高周波に於ける表皮効果の影響は周波数の平方根に比例、 高周波に於ける近接効果の影響は周波数に関係なく導体間隔だけで決まります。 つまり、導体群全体のインピーダンスに与える影響としては、 インダクタンスが最大で、表皮効果が二番目、最後が近接効果になります。 巷に溢れる誤った説明は、この理解が抜けているようです。
TEM mode の電磁波を使う伝送線路では往復2導体が必要ですが、 集合導体を同軸線路の中心導体として配置すれば、 環路導体との相互インダクタンスを考慮しなくて済みます。 回路計算としては、このほうが楽ですが、 実用的には往復並行導体のほうが多いので、 往路の影響がわかりやすいように、 往路を考慮することにしました。
TEM (Transverse Electromagnetic Mode) は電磁波の伝搬形態の一つで、 電界と磁界方向が電磁波の進行方向と直交した形態ですが、 往復2導体で構成される伝送路で使われます。 電磁気学の教科書には必ず出ていますので、 忘れていたら見直してみてください。
三角関数で個々の素線間の相互インダクタンスを計算して合計しても良いのですが、 Maxwell 創案の GMD (Geometric Mean Distance - 幾何学的平均距離)
(A+B+C+ ..)*log(R) = A*log(Ra) + B*log(Rb) + C*log(Rc) + .. ここに A, B, C, .. = 注目面積以外の導体個々の面積 Ra, Rb, Rc, .. = 注目面積と個々の面積 A, B, C, .. との GMD R = 注目面積と面積 A, B, C, .. の全てとの GMDを使うと極めて簡単になります。
外周素線 1 本を考えることにして、 その隣接外周導体 2 本までの距離と中心導体との距離はすべて d、 1 本先の外周導体 2 本までの距離が sqrt(3)*d、 反対側の外周導体までの距離が 2*d ですから、 外周素線 1 本と残りの全導体間の GMD (Geometric Mean Distance - 幾何学的平均距離) は
(d * sqrt(3)*d * 2*d * sqrt(3)*d * d)^(1/6) = d * 6^(1/5)ですから、 2 導体間の相互インダクタンスの計算に変換できてしまいます。
古くから有名な実測値は
A.E.Kennelly, F.A.Laws and P.H.Pierce,- Experimental Researches on Skin effect in conductors, Trans. Ann. I.E.E. 34, 1915, p1953-2021と、
A.E.Kennelly and H.A.Affel,- Skin-Effect Resistance Measurement of Conductors, Proceedins of the Institute of Radio Engineers, May, 1917 p523-555です。
近接効果まで考慮した 7 芯導体のインピーダンス計算については、 http://www.intex.tokyo/text/skin-effect/をご覧ください。
平林 浩一 2017-09