平板導体の渦電流問題 (9)

他の導体から十分離れた場所にある円柱や円筒断面の導体の電流分布は 中心軸に対して対称、 すなわち、同一円周上で一様ですが、 断面が歪むと対称ではなくなります。

電流が集中するのは中心から離れた場所で、 多くの導体構造について高精度の測定を行った A.E.Kennelly は この現象を(平板導体の)Edge effectと呼びました。

1. 薄肉楕円導体

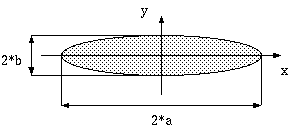
１図 - 薄肉楕円導体

歪んだ円として最も素直な形状である楕円(oval)については 短軸(minor axis)が侵入深さより小さい場合の解析的近似解が知られていて、 下記のようになります。 (注１)

  Zac/Rdc = Jk(k) / Jk'(k)                                                (1)
  ここに、
	Zac = 楕円導体の内部インピーダンス (Ω/m)
	Rdc = 楕円導体の直流抵抗 (Ω/m)
	Jk(x) = k 階の Bessel 関数
	jk'(x) = (d/dx)Jk(x) .. Jk(x) の微分
	k = j * m
	j = sqrt(-1)
	m = j * ω * μ / (4 * π * Rdc)
	Rdc = 1.0 / (g * π * a * b)
	g = 導体の導電率 (S/m) .. 電気銅なら 5.80e7
	μ = 導体の透磁率 (H/m) .. 電気銅なら 4e-7π (非磁性)
	a = 楕円の半長軸 (semi-major axis)
	b = 楕円の半短軸 (semi-minor axis)
	ω = 2 * π * f .. 角周波数 (rad/s)
	f = 周波数 (Hz)
	π = 3.1415.. 円周率

   2 * b « sqrt(2.0 / (ω * μ * g))

(1) 式の Bessel 関数は変数だけでなく、 階数も複素数ですから、 計算はたいへんそうですが、 次ぎのような連分数展開(continued fraction expansion)が可能です。

  z = lim[1;2/x,4/x,...,2*n/x]                                            (2)
      n→∞
          1
    = 1 + --------  1
          2/x + 1 + -------
                    4/x + 1 +  ...
  ここに
	z = Jk(k) / Jk'(k)

      o--R--+--R--+--R--+--R--
         |     |     |     |
  z ->  2L    4L    6L    8L  ...
         |     |     |     |
      o--+-----+-----+-----+--
  R = 1,  L = m

  z = Γ(1/3)/(2^(1/3)*3^(1/3))*Γ(2/3)*m^(1/3)
    = 0.942.. + j*0.544...)*m(1/3)

  z = 1 + m / 2 - m^2 / 3

楕円導体の Edge Effect による交流抵抗の増加は、 平板導体の dge Effect による交流抵抗の 2 倍程度になります。

2. 平板導体

薄肉平板導体(rectangular strip)については、 H.B.Dwight による多項式近似(注２)がありますが、 ここでは、より一般性のある 積分方程式(integral equation)の数値解法を説明します。

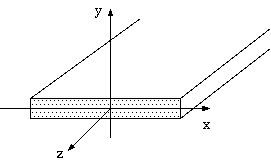
２図 - 方形断面導体

２図の方形断面導体で電流が z 方向に流れている場合を考えます。 ベクトルポテンシャル(Vector Potential) (注３) で表した電磁場の基本的な関係

  E = ∂A/∂t - ∂V/∂z
  ここに
	E = 電界強度 (/m)
	A = ベクトルポテンシャル (weber/m)
	∂x/∂t = x の時間微分
	∂x/∂z = x の z 方向偏微分

  J = -g * ∂V/∂z - g*∂A/∂t
  ここに
	g = 導電率 (S/m)
	A = ベクトルポテンシャル (weber/m)
	∂x/∂t = x の時間微分
	∂x/∂z = x の z 方向偏微分

  A = μ/(2*π)∫J*log(r)*dS
  ここに
	J = 電流密度 (A/m^2)
	S = 断面素片 (m^2)

  J = -μ*g/(2*π)*∫∫(∂J/∂t)*log(sqrt((x-u)^2+(y-v)^2)*du*dv + g*E0

  J(x,y) = -j*ω*μ*g/(2*π)*∫∫J(u,v)*log(sqrt((x-u)^2+(y-v)^2)*du*dv + g*E0

積分方程式の利点は微分方程式で不可欠な境界条件 (boundary condition)が要らないことです。 つまり、積分方程式は、それ自体で完結した世界になります。

ここで、J(u,v) が一定と見做せるサイズ、 つまり、表皮深さより十分小さな面積に離散化すると

  Jm = -j*ω*μ*g/(2*π)*ΣJn*∫∫log(sqrt((x-u)^2+(y-v)^2))*du*dv + g*E0
                         n
  ここに
	m, n = 断面の m, n 番目の区画
	Jm = m 番目の区画の電流密度
	Jn = n 番目の区画の電流密度

さらに、Maxwell の幾何学的平均距離(GMD - Geometric Mean Distance) (注５)

  log(R) = 1/(Si*Sj)*∫∫log(r)*dSi*dSj
  ここに
	R = 面積 Si と面積 Si の領域間の幾何学的平均距離 (m)

  Jm = -j*ω*μ*g/(2*π)*Σ(Jn*Dmn) + g*E0
                         n
  Dmn = Sm*Sn*log(Rmn)
  ここに
	Rmn = 面積 Sm の図形と面積 Sn の図形の幾何学的平均距離

つまり、線形代数(linear algebra)表現なら

  (U + j*X) * J = G
  ここに
	U = 単位行列
	U + j*X = インピーダンス行列 (複素数)
	X = ω*μ*g/(2*π)*ΣDmn
	J = 電流ベクトル (複素数)
	G = 電圧ベクトル (g*E0 + j*0)

この方法はいかなる形状にも対処できる有効な手段です。

3. 隣接平板往復導体

他の導体から遠く離れた平板導体では 周波数が高くなると電流が端部に偏る Edge effectを生じますが、 二つの平板導体を隣接して並べた平板往復導体では、 edge effect より、 他の導体との相互インダクタンスや近接効果の影響が強くなります。

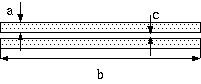
３図 隣接平板往復導体

H.B.Dwightmは次の結果を得ました。 (注６)

  Zac/Rdc = (1 + j*m/2! + (j*m)^2/4! + .. (jm)^n/(2*n)! + ..)
	/ (1 + j*m/3! + (j*m)^2/5! + .. (jm)^n/(2*n+1)! + ..)
  ここに
	m = ω*μ*g*a^2
	  = ω*μ/Rdc
	ω = 2*π*f
	f = 周波数 (Hz)
	μ = 導体の透磁率 (H/m)
	g = 導体の導電率 (S/m)
	a = 導体の厚さ (m)

4. 高周波の場合

高周波になると、いかなる導体形状でも 電磁波が導体表面のごく一部にしか存在しなくなるため、 導体表面の外周形状と (表皮深さと導電率で決まる)表面インピーダンス(surface impedance)、 導体配置だけで決まってしまうのですが、 往復２導体から構成される送電線に沿って伝搬する電磁波は TEM 波(Transverse Electric Magnetic Modes)と呼ばれるもので、 電場と磁場が進行方向に直交し、 伝送路の断面では静電場に見えるため、 静電界の問題に転化することができて、 下記の手順で導体内部インピーダンスを求めることができます。

1. 静電界の Laplace 方程式を解いて、送電線断面空間の電位分布 V(x,y) を求める。

2. 導体の表面電荷密度を求める

  ρ = ε*dV(x,y)/dn
  ここに
	ρ = 導体の表面電荷密度 (coulomb/m^2)
	ε = 誘電体の誘電率 (dielectric constant)
	dV/dn = 導体表面電位の V の法線(表面に垂直)方向微分 (normal)

3. 表面電流密度を求める

  i = ρ/sqrt(ε*μ)
  ここに、
	i = 電流密度 (A/m^2)
	μ = 透磁率 (H/m)

4. 個々の導体について、電力損失を求める

  P = ∫Rs*i^2*dl
  ここに
	P = 導体の電力損失(Joul 熱) (W)
	Rs = 導体の表面インピーダンス (Ω/m)
	   = sqrt(ω*μ/g)
	∫x*dl = x の表面上１周積分

5. 個々の導体について全電流を求める

  I = ∫i*dl
  ここに、
	I = 導体の全電流 (A)
	∫x*dl = x の表面上１周積分

6. 個々の導体について導体抵抗を求める

  R = P / I^2
  ここに、
	R = 導体抵抗 (Ω/m)

7. 個々の導体について導体内部インダクタンスを求める

  Li = R / ω
  ここに
	Li = 導体内部インダクタンス (H/m)

なお、∫i^2*dl >= (∫i*dl)^2 に注意すれば、 電流分布の偏りがあれば P が増加し、 この増加が近接効果になることがわかります。

この手法は有限要素法(Finit Element Method)などの数値解法に適していて、 使い勝手が良いのですが、 具体的な計算例については、 下記解説をご覧ください。

  有限要素法によるケーブル(電線)の電気設計 (4) 渦電流問題

5. 注

5.1. 注１ - 薄い楕円導体の Edge effect

Kennelly の Edge effect を V.Belevitch は lateral skin effect と呼んでいます。

  V.Belevitch,- The lateral skin effect in a flat conductor
	(Philips teck. Rev. 32. 221-231, No. 6/7/8)

5.2. 注２ - 薄い平板導体の Edge effect

  H.B.DWEIGHT,- Skin Effect of a Return Circuit of Two Adjucent
	Strap Conductors
		(Elec. Jour., April 1916, p157)

  Zac/Rdc = 1.0 + p * (0.5 * j + p * (-0.0149994 + p * (0.003122 * j
	+ p * (0.000532 + p * (-0.0000779 * j
	+ p * (-0.0000096 + p * (0.00000094 * j
	+ 0.00000005)))))));
    / 1.0 + p * (0.0965736 * j + p * (0.0152178 + p * (-0.00218 * j
	+ p * (-0.00259 + p * (0.0000237 * j + p * (0.00000100
	+ p * (0.00000022 *j + 0.00000008 * p)))))));
  ここに
	Zac = 薄板の内部インピーダンス (Ω)
	Rdc = 薄板の直流抵抗 (Ω)
	p = ω * μ / (π * Rdc)
	j = sqrt(-1)

  P.Silvester,- Modal Network Theory of Skin Effect in Flat Conductors
	(Proc IEEE 54, p1147-1151, 1966

5.3. 注３ - ベクトル・ポテンシャル

磁気ベクトルポテンシャル(magnetic vector potential)A

  B = curl(A)

  ∇A = -μ*(J + ∂D/∂t)

5.4. 注４ - Manneback の積分方程式

偏微分方程式で解析が行われてきた渦電流問題に、 始めて積分方程式を適用した論文です。

  Charles Manneback,- An Integral Equation for Skin Effect in Parallel Conductors
	(Journal of Math. and Physics, April, 1922, p123-146)

5.5. 注５ - 幾何学的平均距離

  James Clerk Maxwell,- A Treatise on Electricty & Magnetism, Vol.2
	(Dover Publications, Inc.) ISBN-978-0-486-60637-8, p324-330

直流インダクタンス計算の手段として幾何学的平均距離は極めて強力で、 Maxwell は証明なしでスイスイ計算していますが、 幾何学的平均距離の計算はそう簡単ではありません。

Heaviside が一眼惚れして生涯を捧げることにしたこの著作は、 物理学に革命を起こし、相対論への道をひらくことになります。

5.6. 注６ - 隣接平板往復導体

  H.B.Dwight,- Skin Effect of a Return Circuit of Two Adjacent Strap Conductors
	(The Electric Journal, April, 1916