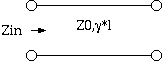
ケーブルのキャパシタンス測定は電子部品のキャパシタンス測定のように インピーダンス測定機にお任せというわけにゆきません。 電子部品のキャパシタンスはそのサイズが仕様が対象とする電磁波の波長に比べて 充分小さいため、 インピーダンス測定機で得られた結果をそのまま利用できますが、 ケーブルは伝送する電磁波の波長に比べてサイズが大きいのが普通で、 低周波の短い線路以外は、 インピーダンス測定機で得られた結果と真の値が一致しないのです。
同じ電気回路のキャパシタンスやインダクタンスでも 電子部品のそれとはまったく別物です。
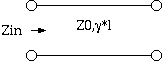
1図 伝送線路のキャパシタンス測定
インピーダンス測定器は終端開放試料の入力アドミタンス Yin (= 1/Zin) を
Yin = G + j*ω*C ここに、 Yin = 入力アドミタンス G = 伝送線路のコンダクタンス (G) ω = 角周波数 (rad/s) C= 伝送線路のキャパシタンス (F/m)と解釈するわけですが、周波数が高くなると、 伝送線路内部の電磁波の位相が一致しなくなって、 G, C ともに導体抵抗やインダクタンスの影響で真の値と一致しなくなります。 そこで、伝送線路の特性を考慮して
C 〜 Cm * β*l/tan(β*l) ここに、 C = キャパシタンスの真の値 (F) Cm = キャパシタンスの測定値 (F) β = 伝送線路の位相定数 (rad/m) l = 伝送線路の長さ (m)で補正することになりますが、 この補正を実行するには位相定数 β の値が必要になります。
この β は同調法により求めた値を使うこともできますが、 同調法で得られる値はかなり高い周波数に対するもので、 測定周波数が低くなると、それより若干小さな値になります。
もう一つのアイデアは、この補正が 周波数とともに増加する Cm を周波数に無関係な一定値にしたい という目的であることを利用して、 C の分散が最小になるβを求めることです。すなわち、 0 < β*l < π/2 の範囲で Cm(f) = C (C は定数) になる β*l を数値計算で探します。
下記のプログラムは F[i], C[i] (i = 0, 1, 2, .. N-1) に、 それぞれ周波数 (Hz) とキャパシタンス測定値 (F) を入れて find_beta(N) を呼び出すと、 適切な β*l を返します。 実験するときは注1のようなプログラムを使ってください。
# 速度係数の決定
# f*x/tan(f*x) 補正したキャパシタンスが一定になる x を求める
# 黄金分割法で分散の極小値を見付ける
# F[i] = 測定周波数 (Hz)、C[i] = キャパシタンス測定値 (F), i = 0, 1, .. N-1
function find_beta(N, i, a, b, c, d, p, y1, y2, x) {
p = (sqrt(5) - 1) * 0.5
a = 1e-10 # 探索範囲の下限
b = PI / F[N - 1] # 探索範囲の上限
c = b - p * (b - a)
d = a + p * (b - a)
y1 = var(c)
y2 = var(d)
for (i = 0; i < 100; i++) {
if ((d - c) / (c + d) < 1e-6)
break
if (y1 < y2) {
b = d
d = c
y2 = y1
c = b - p * (b - a)
y1 = var(c)
}
else if (y1 > y2) {
a = c
c = d
y1 = y2
d = a + p * (b - a)
y2 = var(d)
}
}
return (c + d) / 2 # 分散を最小にする x (= β*l)
}
# C[i] の補正後の分散を求める
function var(x, i, b, c, d, T, Q) {
T = Q = 0
for (i = 0; i < N; i++)
T += C[i]
c = T / N # 平均
T = 0
for (i = 0; i < N; i++) {
b = F[i] * x
d = C[i] * b * cos(b) / sin(b) - c # 分布定数補正誤差
T += d
Q += d * d
}
return (Q - T * T / N) / (N - 1) # 分散
}
この他の方法としては、F[i], C[i] (i = 0, 1, 2, .. N-1) に、 0 < β*l < π/2 の範囲で回帰直線 C = b0 + b1 * F をあてはめ、 b1 = 0 になる β*l を探す方法もあって、 上記と同じ結果が得られます。
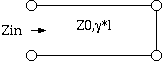
2図 伝送線路のインダクタンス測定
伝送線路のインダクタンスを求める場合もキャパシタンスとまったく同じ 伝送線路補正が使えます。 インピーダンス測定器は伝送線路の入力インピーダンス Zin を
Zin = R + j*ω*L ここに、 Zin = 終端短絡線路の入力インピーダンス R = 伝送線路の抵抗 (Ω) ω = 角周波数 (rad/s) L = 伝送線路のインダクタンス (H)と解釈しますから、
L 〜 Lm * β*l/tan(β*l) ここに、 L = インダクタンスの真の値 (F) Lm = インダクタンスの測定値 (F) β = 伝送線路の位相定数 (rad/m) l = 伝送線路の長さ (m)と補正することになります。 補正の仕方はキャパシタンスとまったく同じです。 この場合も電子部品としてのインダクタのようにインピーダンス測定機で得られた値 がインダクタンスを表すわけではないことを忘れないでください。
3.1. 注1- キャパシタンスの伝送線路補正をテストするプログラム
キャパシタンス測定では測定周波数を試料長で 1/4 波長の 80 % 程度までしか 使わないようにするのが普通ですが、 シミュレーションではもっと広い範囲、 例えば 1 MHz から 1 GHz あたりまで計算して見ると、 いろいろ気づくことがあります。
/usr/bin/awk '
BEGIN {
_Z0 = 75.0
_a = 1.373e-6
_b = 8.385e-12
_v = 1 / sqrt(2.3)
_R = 0.0914
_C = 67.45e-12
l = 1
PI = atan2(0, -1)
N = 0
# インピーダンスアナライザ測定
# 1/4 波長周波数の 80 % 程度までの周波数で測定する
for (i = 1; i <= 35; i++) {
f = i * 1e6
F[N] = f
w = 2 * PI * f
a = _a * sqrt(f) + _b * f
# キャパシタンスモデルでは第2項を入れると誤差が増える
b = w / 2.99792458e8 / _v #+ a
Zoc(_Z0, a, b, l) # 終端開放入力インピーダンス
w = 2 * PI * f
C[N] = -y / w / (x * x + y * y) # キャパシタンス測定値
N++
}
x = find_beta(N) # 伝送線路補正係数の決定
T = 0
for (i = 0; i < N; i++) {
bl = F[i] * x
c = C[i] * bl * cos(bl) / sin(bl) # 補正データ
T += c
print F[i], C[i], c # 周波数、キャパシタンス測定値、伝送線路補正値
}
T /= N
print "Caverage =", T >"/dev/stderr"
exit 0
}
平林浩一, 2016-05