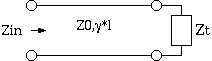
以下、awkによるプログラム例です。 awkの場合は関数の戻り値が一つだけなので、 計算結果は実部を x、虚部を y にセットして戻るようにしています。 一般的な複素数演算は注1にまとめてありますので、 必要なもの、あるいは、このすべてをプログラムに組み込んで使ってください。
計算結果をパイプラインでグラフ生成コマンドに連結する場合、 デバッグ情報を
print .. >"/dev/stderr"と stderr デバイスに出力しておくと、terminal emulator で見ることができます。
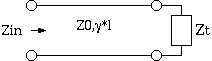
1図 伝送線路の入力インピーダンス
伝送線路の二次定数を
Z0 = z0 + j*0 .. 高周波近似 (10 MHz から数十 MHz 以上) γ = α + j*β線路の終端インピーダンスを
Zt = xt + j*yt線路の長さを l としたとき、線路始端から見た入力インピーダンスは 下記のように書けます。
# Zin = (Zt/Z0 + tanh(γ*l) / (1 + (Zt/Z0)*tanh(γ*l)) * Z0
# α + j*β = x1 * j*y1, Zt = x2* j*y2
function Zin(z0, x1, y1, l, x2, y2, x3, y3, x4, y4) {
Tanh(x1 * l, y1 * l)
x3 = x
y3 = y
Mul(x, y, x2 / z0, y2 / z0)
x4 = x + 1
y4 = y
Add(x3, y3, x2 / z0, y2 / z0)
Div(x, y, x4, y4)
Mul(x, y, z0, 0)
}
終端開放線路の入力インピーダンス Zoc と終端短絡線路の入力インピーダンス Zsc は
# Zoc = Z0 / tanh((α + j * β) * l)
# Z0 = z0 + j*0, α + j*β = x1 + j*y1
function Zoc(z0, x1, y1, l) {
Tanh(x1 * l, y1 * l)
Div(1, 0, x, y)
x *= z0
y *= z0
}
# Zsc = Z0 * tanh((α + j * β) * l)
# Z0 = z0 + j*0, α + j*β = x1 + j*y1
function Zsc(z0, x1, y1, l) {
Tanh(x1 * l, y1 * l)
x *= z0
y *= z0
}
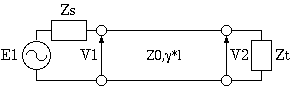
2図 伝送線路の伝送特性
線路の始端と終端の電圧は次ぎのように書けます。
# V1/E1 = ケーブル送端電圧
# γ = x1 * j*y1, Zs = xs + j*ys, Zt = xt + j*yt
function V1(xs, ys, xt, yt, z0, x1, y1, l, x2, y2) {
Zin(z0, x1, y1, l, xs, rs)
x2 = x; y2 = y
Div(x2, y2, x2 + xs, y2 + ys)
}
# V2/E1 = ケーブル受端電圧
# V2 = 1/2 * 1/(cosh(γ*l) + z0/(Zs+Zt)*(1+(Zs*Zt/z0^2))*sinh(γ*l))
# Z0 = z0 + j*0, γ = x1 + j*y1, Zs = xs + j*ys, Zt = xt + j*yt
function V2(xs, ys, xt, yt, z0, x1, y1, l, a, x2, y2, x3, y3) {
Cosh(x1 * l, y1 * l)
x2 = x; y2 = y
Sinh(x1 * l, y1 * l)
x3 = x; y3 = y
coef(z0, xs, ys, xt, yt)
Mul(x, y, x3, y3)
Add(x, y, x2, y2)
Div(1, 0, x, y)
Mul(x, y, xt, yt)
Div(x, y, xs + xt, ys + yt)
}
open/short法は終端開放線路と終端短絡線路の入力インピーダンスから 線路の二次定数を求める手法ですが、 単一試料で任意の周波数に対する測定ができる半面、 1/4 波長近くまでの比較的低い周波数でし使えないのが欠点で、 このプログラムに
/usr/bin/awk '
BEGIN {
# 高周波ケーブルモデル
_Z0 = 75.0 # 特性インピーダンス (Ω)
_a = 1.373e-6 # 減衰 (導体損失)
_b = 8.385e-12 # 減衰 (誘電体損失)
_v = 1 / sqrt(2.3) # 速度係数 (ポリエチレン絶縁)
_R = 0.0914 # 直流抵抗 (Ω/m)
_C = 69e-12 # キャパシタンス (F/m)
l = 1 # 試料長
PI = atan2(0, -1)
offset = p = 0 # 位相定数補正
for (f = 1e6; f <= 1000e6; f += 1e6) {
w = 2 * PI * f # 角周波数 (rad/m)
a = _a * sqrt(f) + _b * f # 減衰定数
b = w / 2.99792458e8 * sqrt(2.3) + a # 位相定数
Zoc(_Z0, a, b, l) # 終端開放入力インピーダンス
x1 = x; y1 = y
Zsc(_Z0, a, b, l) # 終端短絡入力インピーダンス
x2 = x; y2 = y
# Z0
Mul(x1, y1, x2, y2)
Sqrt(x, y)
zx = x; zy = y # Z0 = zx + j*zy
# γ
Div(x2, y2, x1, y1)
Sqrt(x, y)
Atanh(x, y)
x /= l
if (p >= 0.0 && y < 0.0)
offset += PI
p = y # 直前
y /= l
y += offset
gx = x; gy = y # γ = gx + j*gy
print f, zx, zy, gx, gy
}
exit 0
}'
金属導体の高周波に於ける減衰定数は周波数の平方根に比例する ことがわかっていますから、 誤差を含む測定値から真の値を推定するときは、実験値に
α = b1 * sqrt(f) ここに、 α = 減衰定数 (neper/m) b1 = 定数 f = 周波数 (Hz)をあてはめる、つまり、測定値と上記の推定値との誤差分散が最小になるような b1 を求めたいということになります。
こういった解析は回帰分析(regression analysis) と呼ばれ、 求める式が線形の場合は線形代数の行列演算を使うと一般的な結果が得られますが、 ここではawkのようなscript言語で簡単に使えるように、
y = a * x + bといった一次式をあてはめる 初歩的なプログラム例を入れておきます。
# 回帰分析 (1独立変数)
# Y[i] = b0 + b1 * X[i] (i = 1, 2, .. N)
function reg1(N, \
i, x1, y1, x2, y2, tx, ty, qx, qy, sx, sy, cxy, a, b, ve) {
tx = ty = qx = qy = cxy = offset = 0
for (i = 0; i < N; i++) {
tx += X[i]
ty += Y[i]
qx += X[i] * X[i]
qy += Y[i] * Y[i]
cxy += X[i] * Y[i]
}
sx = qx - tx * tx / N
sy = qy - ty * ty / N
cxy -= tx * ty / N
b1 = cxy / sx
b0 = ty / N - a * (tx / N)
ve = (sy - cxy * cxy / sx) / (N - 2)
return ve # 分散
}
i = 0, 1, .. N-1 として、
Y[i] に従属変数(目的関数)、X[i] に独立変数(説明変数)をセットして
上記のプログラム reg1(N) を実行すると、
Y = b0 + b1 * Xの b0, b1 と誤差分散 ve が得られます。
ケーブルの誘電体損失が大きいと 誘電損率が周波数に依存しないとき
α = b1 * sqrt(f) + b2 * fが現実に近くなりますので、独立変数が2つ必要なりますが、 この場合は i = 0, 1, .. N-1 として、 Y[i] に従属変数(目的関数)、X1[i] と X2[i] に独立変数(説明変数)をセットして 下記のプログラム reg2(N) を実行すると、
Y = b0 + b1 * X1 + b2 * X2の b0, b1, b2 が得られます。 ただ、ポリエチレン容器を電子レンジに入れてみれば、 b2 はかなり小さいだろうという実感が得られると思います。
# 2変数の重回帰分析
# y = b0 + b1 * X1[] + b2 * X2[]
function reg2(N, T1, T2, Ty, S11, S22, S12, Syy, S1y, S2y) {
T1 = T2 = Ty = S11 = S22 = S12 = Syy = S1y = S2y = 0
for (i = 0; i < N; i++) {
T1 += X1[i]
T2 += X2[i]
Ty += Y[i]
S11 += X1[i] * X1[i]
S22 += X2[i] * X2[i]
S12 += X1[i] * X2[i]
Syy += Y[i] * Y[i]
S1y += X1[i] * Y[i]
S2y += X2[i] * Y[i]
}
Ty /= N; T1 /= N; T2 /= N # 平均
# T1 = T2 = Ty = 0 # y = b1 * X1 + b2 * X2 (b0 = 0) model
S11 -= N * T1 * T1 # 変動
S22 -= N * T2 * T2
S12 -= N * T1 * T2 # 共変動
Syy -= N * Ty * Ty
S1y -= N * T1 * Ty
S2y -= N * T2 * Ty
b1 = (S1y * S22 - S2y * S12) / (S11 * S22 - S12 * S12)
b2 = (S2y * S11 - S1y * S12) / (S11 * S22 - S12 * S12)
b0 = Ty - b1 * T1 - b2 * T2
return
}
ここで、 キャパシタンスの伝送線路補正で必要になる
y = c ここに、 c = 定数という直線をあてはめる場合を考えてみます。つまり、測定誤差 ei が
e1 = y1 - b0 e2 = y2 - b0 .. ei = yi - b0のとき、Σei^2 の和を最小にする b0 と、その誤差分散を求める問題です。
n n
Q = Σei^2 = Σ{yi - b0)^2}
i=1 i=1
を b0 で偏微分した結果が 0 になるとき Q が極小になりますから、
n
(∂/∂b0)(Q) = -2 * Σ{yi - b0} = 0
i=1
を解いて
n
b0 * n = Σyi
i=1
つまり、b0 は測定結果の平均値なのです。
普通、回帰分析の説明では定数をあてはめるなどといったことは話題にしませんが、 これを考えると、平均の意味がはっきりしますし、 回帰分析自体が多次元の平均操作になっていることが実感できると思います。
以下、この 0 次元の回帰直線を求める、つまり、 平均と分散を求める script 例も入れておきます。
# X[i] (i = 0, 1, .. N-1) の平均と分散
function reg0(N, i, T, Q, S, V) {
T = Q = 0
for (i = 0; i < N; i++) {
T += X[i]
Q += X[i] * X[i]
}
S = Q - T * T / N # 変動
V = S / (N - 1) # 分散
# average = T / N # 平均
return V
}
Z = x + j*y # j = sqrt(-1) .. 虚数単位
# complex functions
function Add(x1, y1, x2, y2) {
x = x1 + x2
y = y1 + y2
}
function Sub(x1, y1, x2, y2) {
x = x1 - x2
y = y1 - y2
}
function Mul(x1, y1, x2, y2) {
x = x1 * x2 - y1 * y2
y = x1 * y2 + y1 * x2
}
function Div(x1, y1, x2, y2, r2) {
r2 = x2 * x2 + y2 * y2
x = (x1 * x2 + y1 * y2) / r2
y = (y1 * x2 - x1 * y2) / r2
}
function Exp(x1, y1, a) {
a = exp(x1)
x = a * cos(y1)
y = a * sin(y1)
}
function Log(x1, y1) {
x = 0.5 * log(x1 * x1 + y1 * y1)
y = atan2(y1, x1)
}
function Sqrt(x1, y1, r, w) {
x = 0.5 * log(x1 * x1 + y1 * y1) * 0.5
y = atan2(y1, x1) * 0.5
a = exp(x)
x = a * cos(y)
y = a * sin(y)
}
function Pow(x1, y1, x2, y2, x3, y3) {
Log(x1, y1)
x3 = x
y3 = y
Mul(x3, y3, x2, y2)
Exp(x, y)
}
function Sin(x1, y1, e, f) {
e = exp(y1)
f = 1 / e
x = 0.5 * cos(x1) * (e - f)
y = 0.5 * sin(x1) * (e + f)
}
function Cos(x1, y1, e, f) {
e = exp(y1)
f = 1 / e
x = 0.5 * cos(x1) * (f + e)
y = 0.5 * sin(x1) * (f - e)
}
function Tan(x1, y1, e, f, d) {
e = exp(2 * y1)
f = 1 / e
d = cos(2 * x1) + 0.5 * (e + f)
x = sin(2 * x1) / d
y = 0.5 * (e - f) / d
}
function Sinh(x1, y1, e, f) {
e = exp(x1)
f = 1 / e
x = 0.5 * (e - f) * cos(y1)
y = 0.5 * (e + f) * sin(y1)
}
function Cosh(x1, y1, e, f) {
e = exp(x1)
f = 1 / e
x = 0.5 * (e + f) * cos(y1)
y = 0.5 * (e - f) * sin(y1)
}
function Tanh(x1, y1, e, f, d) {
e = exp(2 * x1)
f = 1 / e
d = 0.5 * (e + f) + cos(2 * y1)
if (d == 0) {
e = exp(x1)
f = 1 / e
x = 0
y = (e + f) * sin(y1)
}
else {
x = 0.5 * (e - f) / d
y = sin(2 * y1) / d
}
}
function Atanh(x1, y1) {
Div(1 + x1, y1, 1 - x1, -y1)
Log(x, y)
x *= 0.5
y *= 0.5
}
function Abs(x, y) {
return sqrt(x * x + y * y)
}
function Arg(x, y) {
return atan2(y, x)
}
誤差要因の評価機能を追加する方法を説明しておきます。
まず、終端開放線路と終端短絡線路の試料長の違いは これらの線路長の比 Kl を定義して、
Kl = lo / ls ここに、 lo = 終端開放線路長 (m) ls = 終端短絡線路長 (m)プログラムへの入力は ls と Kl で与えることにすれば
Zsc(_Z0, a, b, l) を Zsc(_Z0, a, b, Kl * ls) Zoc(_Z0, a, b, l) を Zoc(_Z0, a, b, ls)と書き換えれば済みます。 実際に計算してみると、僅か 1 % の長さの違いが周波数が高くなるにつれて 極めて大きな影響を与えることがわかりますが、 理由は長さの違いが波長との比較になるためです。 ポリエチレン絶縁同軸ケーブル 1 GHz の 1/4 波長は 49 mm ですから、 0.5 mm でも、この 1 % になってしまいます。
終端キャパシタンス Ct (F) と終端インダクタンス Lt (H) は
Zsc(_Z0, a, b, l) を Zin(_Z0, a, b, l, ω*Lt, 0) Zoc(_Z0, a, b, l) を Zoc(_Z0, a, b, l, -1/(ω*Ct)と書き換えれば済みます。
入力キャパシタンス Cs (F) と入力インダクタンス Ls (H) は 計算した試料の入力インピーダンス Zsc() または Zoc() の値を x + j*y とすれば、 Cs の場合は
Div(x, y, 1 - ω*Cs*y, ω*Csx)を追加、Ls の場合は
Add(x, y, ω*Ls, 0)を追加するだけです。
実際に計算してみると、長さの違いだけでなく、 これらのごく僅かな浮遊インピーダンスもまた、 高周波では極めて大きな影響を与えることがわかって、 open/short 法の限界が体感できます。
これらのプログラムは自分で書いて実験してみることをお勧めしなすが、 不精がしたくなったら、 Open-Short法シミュレーションで試してください。 Ct, Tt, Cs, Ls の具体的な値を知りたくなると、 「やはり電磁気学の初歩も必要だなあ」と思えるかもしれません。
平林浩一, 2016-05