有限要素法によるケーブル(電線の電気設計 (2) - 軸対称静電界問題

FreeFEMを使った有限要素法による軸対称の静電界問題について解説します。 軸対称ですから、扱える問題は同軸ケーブルの長さ方向の変化に限定されますが、 不連続点の解析といった重要な応用があります。

1. 円筒座標に於けるラプラス方程式

軸対称問題は円筒座標を使うと半径と長さの２次元問題になりますが、円筒座標 に於ける Laplace 方程式

  (d/dr)^2(e*v) + (1/r)*(d/dr)(e*v) + (d/dz)^2(e*v) = 0
  ここに、
	r = 半径方向の座標
	z = 軸方向の座標
	e = 誘電率

  pde(v) laplace(v)*e + dy(e*v)/y = 0                             (1A)
  pde(v) -laplace(v)*e*y = 0                                    (1B)
  pde(v) dyy(e*v)*y +dxx(e*v)*y + dy(e*v) = 0;                      (1C)

空間に蓄積される静電エネルギは

               2*π
  U = (ε/2)*∫∫(((d/dx)(v))^2 + ((d/dy)(v))^2)*dx*dy
            y 0
 
    = (ε/2)*∫(((d/dx)(v))^2 + ((d/dy)(v))^2)*y*dy
            y
  ε = 誘電率
     = εs*1e7/4/π/(2.99792458)^2 = εs*8.854..e-12
  εs = 比誘電率

  u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
  U:=intt[u];

この式が正しい結果を与えることを 5C-2V 同軸ケーブルについて確認すると、次の ようになります。

/* 5D-2V coaxial cable */
a1:=0.7e-3;	/* inner conductor diameter */
a2:=2.4e-3;	/* outer conductor diameter */
s1:=(a2-a1);	/* length */
e1:=2.3;	/* dielectric constant */

n2:=20;
n1:=floor(s1*n2/(a2-a1));
n3:=n1;
n4:=n2;
border(1,0,n1+n2+n3+n4,n1+n2+n3+n4+1) {
 if (t<=n1) { x:=t*s1/n1; y:=a1; ib:=1 }
 else if (t<n1+n2) { x:=s1; y:=a1+(t-n1)*(a2-a1)/n2; ib:=2 }
 else if (t<=n1+n2+n3) { x:=s1-(t-n1-n2)*s1/n3; y:=a2; ib:=3 }
 else { x:=0; y:=a2-(t-n1-n2-n3)*(a2-a1)/n4; ib:=4 };
};
buildmesh(5000);

e=e1;
solve(v) {
 onbdy(1) v = 1;
 onbdy(2,4) dnu(v) = 0;
 onbdy(3) v = 0;
 pde(v) -laplace(v)*e*y = 0;
};
plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
c0:=intt[u]*17.707;
printf("C=%g pF\n",c0/s1);
printf("exact solution=%g\n",55.63*e1/log(a2/a1));

2. 同軸線路の不連続点の解析

ケーブル伝送の主役である純粋なTEM波(transverse electromagnetic wave)は 長さ方向に一様な伝送線路でのみ伝搬し、線路の不連続部分や一様でないところでは 他のモードと結合して、そこに蓄積されるエネルギは極めて低い周波数に於いてさえ 無視できないことが知られています。

この一見複雑に見える不連続点の影響について、Whinnery と Jamieson が 1944 年に 伝送線路の不均一性が、 「等価不連続キャパシタンス」 (equivalent discontinuity capacitance) として正確に評価できる ことを証明し、簡単かつ強力な解析基盤を確立しました。(注１)

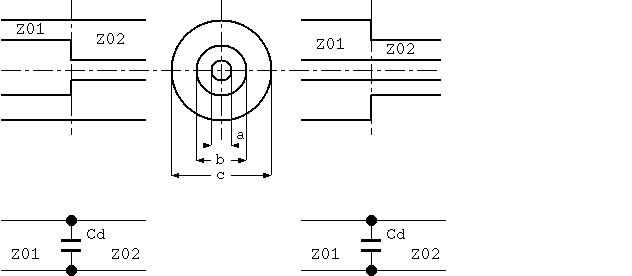
これは、例えば、１図のような同軸線路の不連続点は 特性インピーダンスの異なる２つの線路の接続点に 等価不連続キャパシタンス Cd を接続したものとして計算することができる という意味です。

１図 同軸線路の段階状不連続点とその等価回路

彼らの証明はmode matchingと呼ばれる解析的方法を応用したものですが、 数値計算による解析を使うと極めて簡単になって、例えば、１図の場合は、

  Cd = C0 - C1 - C2
  ここに
	Cd = 等価不連続キャパシタンス (F)
	C0 = 不連続面を含む全領域のキャパシタンス (F)
	C1 = 不連続面のない特性インピーダンス Z01 の線路のキャパシタンス (F)
	C2 = 不連続面のない特性インピーダンス Z02 の線路のキャパシタンス (F)

この場合、C0 は有限要素法等の数値計算で求めることになりますが、 C1 と C2 は数値計算以外に、解析的方法でも計算できることが多く、 特に同軸線路の場合は、

  C = 2*π*ε0*εs*l/log(b/a)
  ここに
	C = 同軸ケーブルのキャパシタンス (F)
	π = 3.14159265..
	ε0 = 真空の誘電率 (F/m)
	    = 1e7/(4*π*2.99792458^2)
	    = 8.854e-12
	εs = 絶縁体の比誘電率
	l = ケーブルの長さ (m)
	b = 外部導体内径 (m)
	a = 内部導体外径 (m)

なお、この方法は 不連続部分の幾何学的寸法が電磁波の波長に比べて十分小さくなければならない ことに注意してください。この条件が、 キャパシタンスという集中回路定数が使えるための基盤になっています。

3 内部導体の階段的変化

１図の左側の構造をFreeFEMで解析すると次のようになります。

/* step discontinuities in coaxial line */
a1:=1;
a2:=3;
a3:=2;

s1:=a2-a3;
s2:=a2-a1;
n2:=20;
d1:=a3-a1;
n1:=floor(s1*n2/d1);
n3:=floor(s2*n2/d1);
n4:=floor((a2-a1)*n2/d1);
n5:=floor((s1+s2)*n2/d1);
n6:=floor((a2-a3)*n2/d1);
border(1,0,n1+n2+n3+n4+n5+n6,n1+n2+n3+n4+n5+n6+1) {
 if (t<=n1) { x:=t*s1/n1; y:=a3; ib:=1 }
 else if (t<=n1+n2) { x:=s1; y:=a3-(t-n1)*(a3-a1)/n2; ib:=1 }
 else if (t<=n1+n2+n3) { x:=s1+(t-n1-n2)*s2/n3; ib:=1 }
 else if (t<n1+n2+n3+n4) { x:=s1+s2; y:=a1+(t-n1-n2-n3)*(a2-a1)/n4; ib:=2 }
 else if (t<=n1+n2+n3+n4+n5) { x:=s1+s2-(t-n1-n2-n3-n4)*(s1+s2)/n5; y:=a2; ib:=3 }
 else { x:=0; y:=a2-(t-n1-n2-n3-n4-n5)*(a2-a3)/n6; ib:=4 };
};
buildmesh(5000);

solve (v) {
 onbdy(1) v = 1;
 onbdy(3) v = 0;
 onbdy(2,4) dnu(v) = 0;
 pde(v) -laplace(v)*y = 0;
};
plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
c0:=intt[u]*17.707;
c1:=55.63/log(a2/a3)*s1;
c2:=55.63/log(a2/a1)*s2;
cd:=c0-c1-c2;
printf("Cd=%g pF\n",cd);

なお、長さ方向に一様な線路のキャパシタンスは線路の構造が幾何学的に相似なら 同じ値になりますが、 不連続等価キャパシタンスは幾何学的に相似でも線路の大きさによって変化します ので注意してください。キャパシタンスとそこに蓄積される静電エネルギ の関係は

  U = C*V^2/2
  ここに
	C = キャパシヤンス (F)
	V = 電圧 (V)
	U = キャパシタンスに蓄えられるエネルギ (J)

例えば、この例では、外部導体の半径が 3 mm になれば、この 1/1000 の値になります。

1.2 外部導体の階段的変化

/* step discontinuities in coaxial line */
a1:=1;
a2:=3;
a3:=2;

s1:=a2-a1;
s2:=a3-a1;
n4:=20;
d1:=a2-a3;
n1:=floor((s1+s2)*n4/d1);
n2:=floor((a3-a1)*n4/d1);
n3:=floor(s2*n4/d1);
n5:=floor(s1*n4/d1);
n6:=floor((a2-a1)*n4/d1);
border(1,0,n1+n2+n3+n4+n5+n6,n1+n2+n3+n4+n5+n6+1) {
 if (t<=n1) { x:=t*(s1+s2)/n1; y:=a1; ib:=1 }
 else if (t<=n1+n2) { x:=s1+s2; y:=a1+(t-n1)*(a3-a1)/n2; ib:=2 }
 else if (t<=n1+n2+n3) { x:=s1+s2-(t-n1-n2)*s2/n3; ib:=3 }
 else if (t<n1+n2+n3+n4) { x:=s1; y:=a3+(t-n1-n2-n3)*(a2-a3)/n4; ib:=3 }
 else if (t<=n1+n2+n3+n4+n5) { x:=s1-(t-n1-n2-n3-n4)*s1/n5; y:=a2; ib:=3 }
 else { x:=0; y:=a2-(t-n1-n2-n3-n4-n5)*(a2-a1)/n6; ib:=4 };
};
buildmesh(5000);

solve (v) {
 onbdy(1) v = 1;
 onbdy(3) v = 0;
 onbdy(2,4) dnu(v) = 0;
 pde(v) -laplace(v)*y = 0;
};
plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
c0:=intt[u]*17.707;
c1:=55.63/log(a2/a1)*s1;
c2:=55.63/log(a3/a1)*s2;
cd:=c0-c1-c2;
printf("Cd=%g pF\n",cd);

4 同軸線路のサイズ変換

同軸線路のサイズを変更しようとすると、一様性が失われますから、 不連続等価キャパシタンスができてしまうのは防げませんが、変換部分の構造によって 不連続等価キャパシタンスの大きさも異なりますから、設計に際しては なるたけこれが小さくなるように最適化が必要です。

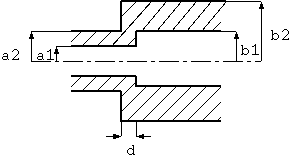
２図 同軸線路のオフセット突合わせジョイント

サイズ変換でよく使われるのは ２図のように内部導体と外部導体の不連続部分をずらせた構造で、 この場合は オフセットの大きさに最適値があって、それより小さくても大きく ても不連続等価キャパシタンスは増加します。

例えば、誘電体の比誘電率が 2.0 で、特性インピーダンス 50 Ohm、導体の サイズ比が１：２の変換コネクタを設計するとして、そのサイズを下記のようにとれば、 オフセット d が 1.14 mm のとき、不連続等価キャパシタンスが最小になります。

  a1 = 1.524 mm
  a2 = 4.95 mm
  b1 = 3.05 mm
  b2 = 9.91 mm

/* offset butt junction in coaxial line */
a1:=0.762e-3;	/* inner diameter (1) */
a2:=1.524e-3;	/* outer diameter (1) */
b1:=2.477e-3;	/* inner diameter (2) */
b2:=4.953e-3;	/* outer diameter (2) */
d1:=1.143e-3;	/* offset */

s1:=a2-a1;
s2:=b2-b1;
d2:=b1-a1;
n2:=20;
n1:=floor((s1+d1)*n2/d2);
n3:=floor(s2*n2/d2);
n4:=floor((b2-b1)*n2/d2);
n5:=floor((s2+d1)*n2/d2);
n6:=floor((b2-a1)*n2/d2);
n7:=floor(s1*n2/d2);
n8:=floor((a2-a1)*n2/d2);

border(1,0,n1+n2+n3+n4+n5+n6+n7+n8,n1+n2+n3+n4+n5+n6+n7+n8+1) {
 if (t<=n1) { x:=t*(s1+d1)/n1; y:=a1; ib:=1 }
 else if (t<=n1+n2) { x:=s1+d1; y:=a1+(t-n1)*(b1-a1)/n2; ib:=1 }
 else if (t<=n1+n2+n3) { x:=s1+d1+(t-n1-n2)*s2/n3; y:=b1; ib:=1 }
 else if (t<n1+n2+n3+n4) { x:=s1+d1+s2; y:=b1+(t-n1-n2-n3)*(b2-b1)/n4; ib:=2 }
 else if (t<=n1+n2+n3+n4+n5) {
  x:=s1+d1+s2-(t-n1-n2-n3-n4)*(s2+d1)/n5; y:=b2; ib:=3 }
 else if (t<=n1+n2+n3+n4+n5+n6) {
  x:=s1; y:=b2-(t-n1-n2-n3-n4-n5)*(b2-a2)/n6; ib:=3 }
 else if (t<=n1+n2+n3+n4+n5+n6+n7) {
  x:=s1-(t-n1-n2-n3-n4-n5-n6)*(a2-a1)/n7; y:=a2; ib:=3 }
 else { x:=0; y:=a2-(t-n1-n2-n3-n4-n5-n6-n7)*(a2-a1)/n8; ib:=4 };
};
buildmesh(5000);

solve (v) {
 onbdy(1) v = 1;
 onbdy(3) v = 0;
 onbdy(2,4) dnu(v) = 0;
 pde(v) -laplace(v)*y = 0;
};
plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
c0:=intt[u]*17.707;
c1:=55.63/log(a2/a1)*s1;
c2:=55.63/log(b2/b1)*s2;
cd:=c0-c1-c2;
printf("Cd=%g pF\n",cd);

5 同軸線路のバンドパス・フィルタ

マイクロ波(microwave)のバンドパス・フィルタとして、中心導体にギャップを作った 同軸線路がよく使われますが、その構造と等価回路は３図(a) のようになります。 つまり、中心導体にギャップを作ると、π型フィルタになります。

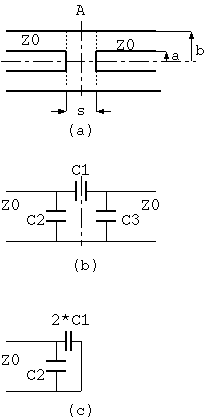
層軸線路の直列ギャップとその等価回路

３図(a) の等価回路が３図(b) ですが、この C1 と C2 を分離して計算するには、 ギャップ中央の A 面に電気壁(electric wall) を追加して外部導体と同じ電位にすれば ３図(c) の等価回路になって、不連続等価キャパシタンスの値は 2*C1+C2 になり、 A 面に磁気壁(magnetic wall) を置いてその左側だけを考えれば、 不連続等価キャパシタンスの値が C2 になりますので、２度に分けて計算すれば 次のようになります。(注３)

/* series gap in coaxial line */
a2:=2.0;	/* outer conductor radius */
a1:=a2/2.0;	/* inner conductor radius */
b1:=0.5*0.2*a2;	/* cavity gap */

b2:=a2*0.6;

n2:=50;
n1:=floor(b2/a1*n2);
n3:=floor(b1/a1*n2);
n4:=floor(a2/a1*n2);
n5:=floor((b1+b2)/a1*n2);
n6:=floor((a2-a1)/a1*n2);
border(1,0,n1+n2+n3+n4+n5+n6,n1+n2+n3+n4+n5+n6+1) {
 if (t<=n1) { x:=t*b2/n1; y:=a1; ib:=1 }
 else if (t<=n1+n2) { x:=b2; y:=a1-(t-n1)*a1/n2; ib:=1 }
 else if (t<n1+n2+n3) { x:=b2+(t-n1-n2)*b1/n3; y:=0; ib:=2 }
 else if (t<n1+n2+n3+n4) { x:=b2+b1; y:=(t-n1-n2-n3)*a2/n4; ib:=3 }
 else if (t<=n1+n2+n3+n4+n5) { x:=b2+b1-(t-n1-n2-n3-n4)*(b2+b1)/n5;  ib:=4 }
 else { x:=0; y:=a2-(t-n1-n2-n3-n4-n5)*(a2-a1)/n6; ib:=5 };
}; 

buildmesh(10000);

solve (v,1) {
 onbdy(1) v = 1;
 onbdy(3) v = 0;
 onbdy(4) v = 0;
 pde(v) -laplace(v)*y = 0;
};

plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
u3:=intt[u];
c0:=55.63/log(a2/a1)*b2;
c3:=u3*17.707-c0;

solve (v,1) {
 onbdy(1) v = 1;
 onbdy(3) dnu(v) = 0;
 onbdy(4) v = 0;
 pde(v) -laplace(v)*y = 0;
};

plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
u2:=intt[u];
c2:=u2*17.707;

c2:=u2*17.707-c0;
printf("c2=%g pF\n", c2);
c1:=(c3-c2)*0.5;
printf("c1=%g pF\n", c1);

6 終端開放同軸線路のフリンジ・キャパシタンス

6.1 高周波測定のインピーダンス標準

高周波測定のインピーダンス標準としては、普通 0 Ohm (short), 50 Ohm (load), 0 G (open) の３つが使われますが、同軸線路の終端開放部分にも 不連続等価キャパシタンスがありますから、 完全な open (無限大のインピーダンス) を作るのは不可能で、 例えば、高周波測定で使われる４図のような 0G (open) 標準は、 キャパシタンスとして機能することになり、当然、 測定機内部でもキャパシタンスとして扱います。

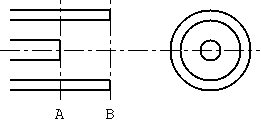
４図 Open インピーダンス標準

例えば、7 mm コネクタの場合なら、次のように約 80 fF のキャパシタンスになります。 (注３)

/* open standard */
a2:=3.5e-3;
a1:=a2/2.28;

s1:=a2-a1;
s2:=a2*2;
n2:=10;
n1:=floor(s1*n2/a1);
n3:=floor(s2*n2/a1);
n4:=floor(a2*n2/a1);
n5:=floor((s1+s2)*n2/a1);
n6:=floor((a2-a1)*n2/a1);
border(1,0,n1+n2+n3+n4+n5+n6,n1+n2+n3+n4+n5+n6+1) {
 if (t<=n1) { x:=t*s1/n1; y:=a1; ib:=1 }
 else if (t<=n1+n2) { x:=s1; y:=a1-(t-n1)*a1/n2; ib:=1 }
 else if (t<=n1+n2+n3) { x:=s1+(t-n1-n2)*s2/n3; y:=0; ib:=2 }
 else if (t<n1+n2+n3+n4) { x:=s1+s2; y:=(t-n1-n2-n3)*a2/n4; ib:=3 }
 else if (t<=n1+n2+n3+n4+n5) { x:=s1+s2-(t-n1-n2-n3-n4)*(s1+s2)/n5; y:=a2; ib:=4 }
 else { x:=0; y:=a2-(t-n1-n2-n3-n4-n5)*(a2-a1)/n6; ib:=5 };
};
buildmesh(5000);

solve (v) {
 onbdy(1) v = 1;
 onbdy(4) v = 0;
 onbdy(3,4,5) dnu(v) = 0;
 pde(v) -laplace(v)*y = 0;
};
plot(v);

u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
c0:=intt[u]*17.707;
c1:=55.63/log(a2/a1)*s1;
cd:=c0-c1;
printf("Cd=%g pF\n",cd);

なお、この開放線路の端部に生ずる不連続等価キャパシタンスは fringing capacitanceと呼ぶのが普通です。 また、load や Short の標準については、不連続等価キャパシタンスによる インピーダンスは、50 Ohm, 75 Ohm, 0 Ohm に比べて無視できますので、 問題になりません。

6.2 同軸ケーブルのフリンジ・キャパシタンス

3C-2V 同軸ケーブルの終端キャパシタンスを求めた例です。

/* fringe capacitance, 3C-2V */
a1:=0.5e-3/2;
a2:=3.1e-3/2;
a3:=3.8e-3/2;
a4:=a3*2;
b1:=a1*10;
b2:=a1*30;
n2:=5;
n1:=floor(b1*n2/a1);
n3:=floor((b2-b1)*n2/a1);
n4:=floor(a4*n2/a1);
n5:=floor(b2*n2/a1);
n6:=floor((a4-a3)*n2/a1);
n7:=n1;
n8:=floor((a3-a2)*n2/a1);
n9:=n1;
n10:=floor((a2-a1)*n2/a1);
e1:=2.3;
e2:=1;
border(1,0,n1+n2+n3+n4+n5+n6+n7+n8+n9+n10,n1+n2+n3+n4+n5+n6+n7+n8+n9+n10+1) {
  if (t<=n1) { x:=t*b1/n1; y:=a1; ib:=1 }
  else if (t<=n1+n2) { x:=b1; y:=a1-(t-n1)*a1/n2; ib:=2 }
  else if (t<=n1+n2+n3) { x:=b1+(t-n1-n2)*(b2 - b1)/n3; y:=0; ib:=3 }
  else if (t<n1+n2+n3+n4) { x:=b2; y:=(t-n1-n2-n3)*a4/n4; ib:=4 }
  else if (t<=n1+n2+n3+n4+n5) { x:=b2-(t-n1-n2-n3-n4)*b2/n5; y:=a4; ib:=5 }
  else if (t<=n1+n2+n3+n4+n5+n6) {
	x:=0; y:=a4-(t-n1-n2-n3-n4-n5)*(a4-a3)/n6; ib:=6 }
  else if (t<=n1+n2+n3+n4+n5+n6+n7) {
	x:=(t-n1-n2-n3-n4-n5-n6)*b1/n7; y:=a3; ib:=7 }
  else if (t<=n1+n2+n3+n4+n5+n6+n7+n8) {
	x:=b1; y:=a3-(t-n1-n2-n3-n4-n5-n6-n7)*(a3-a2)/n8; ib:=8 }
  else if (t<=n1+n2+n3+n4+n5+n6+n7+n8+n9) {
	x:=b1-(t-n1-n2-n3-n4-n5-n6-n7-n8)*b1/n9; y:=a2; ib:=9 }
  else { x:=0; y:=a2-(t-n1-n2-n3-n4-n5-n6-n7-n8-n9)*(a2-a1)/n10; ib:=10 };
};
border(1,0,n10,n10+1) { x:=b1; y:=a2-t*(a2-a1)/n10; ib:=10 };
buildmesh(20000);
e=one(region==0)*e1 + one(region==1)*e2;
solve (v) {
 onbdy(1,2) v = 1;
 onbdy(4,5,6) v = 0;
 onbdy(7,8,9) v = 0;
 pde(v) -laplace(v)*y*e = 0;
};
plot(v);
u=0.5*(dx(v)*dx(v)+dy(v)*dy(v))*2*pi*y;
u2:=e2*intt(1)[u];
c:=u2*17.707;
printf("Cd=%g pF\n",c);

u0:=e1*intt(0)[u]+e2*intt(1)[u];
u1:=e1*intt(0)[u];
c0:=intt[u]*17.707;
c0:=u0*17.707;
c1:=e1*55.63/log(a2/a1)*b1;
cd:=c0-c1;
printf("Cd=%g pF\n",cd);
/*
c1:=u1*17.707;
printf("Cd=%g pF\n",c0-c1);
*/

7 インピーダンス測定に於ける試料の接続部分の補正

伝送線路の不連続部分や一様性が失われる部分が回路的には 不連続等価キャパシタンスで表現できるという事実は、 高周波測定に於ける重要な応用があります。

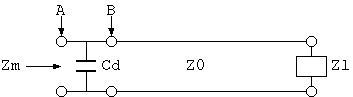
５図 ケーブルの入力インピーダンスの測定

例えば、５図のようなケーブルの入力を測定すつとき、測定機の校正面 A にケーブル 端面 B を接続すると、コネクタを含むその接続部で必ず不連続部分ができます。

この接続部分の影響の評価はちょっと考えると極めて難しそうですが、 この部分も不連続等価キャパシタンスとして扱えることに気づけば、

  Zm = 1/(j*ω*Cd + 1/Zin)
  ここに
	Zm = 入力インピーダンスの測定値 (Ohm)
	j = sqrt(-1)
	ω = 2*π*f = 各速度 (rad/s)
	f = 周波数 (Hz)
	Cd = 不連続等価キャパシタンス (F)
	Zin = ケーブルの入力インピーダンス (Ohm)

  Zin = 1/(1/Zm - j*ω*Cd)

不連続等価キャパシタンスがうまく測定できない場合は、Zm の周波数特性の変動を 最小にする(Smith chart 上で考えればインピーダンス軌跡が小さくまとまる)ような Cd を計算することで推定することができます。

8 平衡ケーブルの開放終端

FreeFEMでは解析できませんが、２芯平衡ケーブルの開放終端の 不連続等価キャパシタンスのアナログ計算が行われていて、次の近似式が得られて います。(注４)

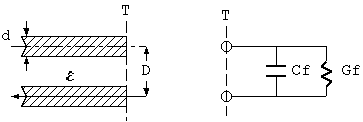
６図 ２芯平衡ケーブルの開放終端

  Cf/C0 = D/(-3.954 + sqrt((2.564*acosh(D/d))^2 + 3.954^2)
  Gf = η*(β*D)^4*((Cf/C0)/D)^2/(12.0*π)
  ここに
	Cf = 不連続等価キャパシタンス (F)
	C0 = 線路のキャパシタンス (F/m)
	Gf = 不連続等価コンダクタンス (G)
	η = 媒質の固有インピーダンス (Ohm)
	   = sqrt(μ/ε)
	μ = 媒質の透磁率 (H/m)
	ε = 媒質の誘電率 (F/m)
	β = ケーブルの伝搬定数 (rad/m)

不連続等価コンダクタンスはケーブル端からの電磁波放射によるエネルギ損失に相当 し、ηの値は空気なら 120*π (約 377) Ohm です。

9. 注

9.1 注１ - 不連続等価キャパシタンス

J.R.Whinnery and H.W.Jamieon,"Equivalent circuits for discontinuities in
  transmission lines", Proc IRE, vol.32,pp.98-114,1944

J.R.Whinnery, H.W.Jamieson, and T.E.Robbines,"Coaxial line discontinuities",
  Proc.IRE,vol.32,pp.695-709,1944

P.Silvester, Ivan A.Cermak,"Analysis of Coaxial Line Discontinuities
by Boundary Relaxation", IEEE Transaction on Microwave Theory and Techniques,
Vol. MTT-17, No.8, Aug. 1969

9.2 注２ - 電気壁と磁気壁

電気壁(electric wall)は完全導体(導電率無限大)の境界で 磁束密度の法線成分が 0 (ｎ・Ｂ＝０)、 磁気壁は完全磁性体(透磁率無限大)による境界で 磁界の法線と垂直方向の成分が 0 (ｎ×Ｈ＝０)です。

電気壁の場合が壁の接線方向の電界成分がありませんから壁は等電位面、 磁気壁の場合は磁界の接線方向成分がありませんから電界は壁に垂直で、 FreeFEMの記法では次のようになります。

  onbdy(n) v=const;	/* 電気壁 */
  onbdy(n) dnu(v)=0;	/* 磁気壁 */

9.3 注３ - Open 標準

B.Bianco, A.Corana, L.Gogiaso and S.Ridella,"Open-circuited coaxial lines as
standards for microwave measurements", Electron. Lett, 19(May), 10, pp.373-374

  C = 79.7/sqrt(1 - (f/34450)^2)
  ここに
	C = キャパシタンス (fF)
	f = 周波数 (MHz)

9.3 注４ - ２芯平衡ケーブルの開放終端

この問題は、

H.E.Green and J.D.Cashman, "End Effect in Open-Circuited Two-Wire Transmission
Lines", IEEE Trans on Microwave Theory and Techniques, vol.MTT-34, No.1,
Jan. 1986