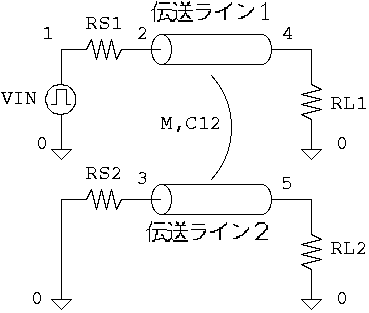
1図 相互インダクタンスと相互キャパシタンス結合を持つ2つの回路
電子回路の高速化とともに、 伝送ラインのクロストーク(cross-talk 漏話)が重要な問題になって、 その評価が必要になることが多く、以下、その要領を解説します。 ここでは、フラットケーブルを題材にしていますが、電線の他の構造とか、 プリント基板等、他の伝送ラインでも、まったく同じです。
回路的には、クロストークの原因は、

1図 相互インダクタンスと相互キャパシタンス結合を持つ2つの回路
伝送ラインとしては、2図のような PVC 絶縁4芯フラットケーブルを使うことにして、 意図する信号伝送は、ノード番号 2, 4 の導体と、それに隣接する 0, 0 の導体で行い、 その信号が隣接する 3, 5 の導体と残りの 0, 0 の導体を使う回路に、 いかなる影響を与えるかを考えることにしましょう。
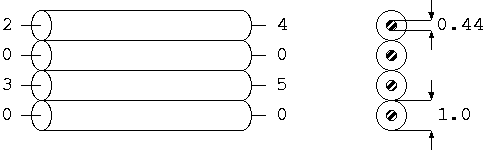
2図 4芯フラットケーブルの導体割り当て
まず、2, 4, 0, 0 の回路と 3, 5, 0, 0 の回路について、 伝送ラインを分布定数回路として扱うためのパラメータ(回路定数)
R = 導体抵抗 (Ohm/m) L = (自己)インダクタンス (H/m) G = コンダクタンス (S/m) G = コンダクタンス (S/m) C = キャパシタンス (F/m) M = 相互インダクタンス (H/m) C12 = 相互キャパシタンス (F/m)を求めなければなりませんが、通常の伝送回路では、導体と誘電体の損失は小さくて、 クロストークに与える影響は少ないうえに、クロストークを減らす方向に働きますから、 R, G を無視、 つまり、無損失とすれば、 3図の6つのパラメータを求めればよいことになります。
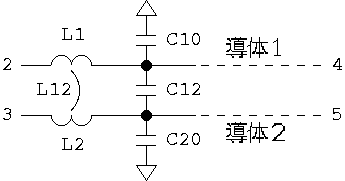
3図 無損失伝送ラインの分布定数回路モデル
これらは、サンプルがあれば、実測で求めることもできますが、ここでは、 優れた有限要素法のプログラム FreeFem++ と、数値計算ツール octave を使うことにして、以下、 行列とベクトルの表記法は原則として octave の文法に従うことにします。
まず、3つのキャパシタンス C1, C2, C12 を求めます。 解析的な計算は無理ですから、 有限要素法や境界要素法等の 数値計算技法を使うことになりますが、最初に、 導体 1 の電位を V、 他の導体の電位を 0 とした境界条件で Laplace 方程式を解いて、
C = Q / V ここに、 C = キャパシタンス (F/m) Q = 導体 1 の電荷 (Q) V = 導体 1 と他の導体との電位差 (V)あるいは、より高い精度が得られる、
C = 2 * W / V^2 ここに、 C = キャパシタンス (F/m) W = (空間全体の)電界のエネルギ (J) V = 導体 1 と他の導体との電位差 (V)から、C11 = C10 + C12 を求め、次に、導体 2 の電位を V、他の導体の電位を 0 として、 C22 = C2 + C12 を求めます。(注3)
最後に、導体 1 と 2 の電位を V、他の導体の電位を 0 として、 C12p = C10 + C20 を求めれば、
C12 = (C11 + C22 - C12p) / 2 C10 = C11 - C12 C20 = C22 - C12から、C10, C12, C20 が得られます。 実測の場合も、同じ手順です。
次に、インダクタンスを求めますが、クロストークが問題になるのは、高周波の場合で、 導体の内部インダクタンスを無視できますから、外部インダクタンスだけを計算することにして、 導体の導電率が十分高く、完全導体とみなすことができて、かつ、誘電体が非磁性体であれば、 誘電体を真空で置き換えた場合のキャパシタンス行列
[ C11 -C12; -C21 C22 ] ここに、 C11 = 導体 1 と他の導体間のキャパシタンス (F/m) C12 = C21 = 導体 1 と導体 2 間の部分容量 (F/m) C22 = 導体 2 と他の導体間のキャパシタンス (F/m) [ a11 a12; a21 a22 ] は octave や scilab の行列表記から、
[ L11 L12; L21 L22 ] = inv([ C11 -C12; -C21 C22])/(2.998e8)^2 ここに、 L11 = 3図の L1 L12 = L21 = 3図の L12 L22 = 3図の L2 2.998e8 = 真空中の光速 (m/s) inv(x) = x の逆行列 (octave や scilab の表記法)として求めるのが簡単です。(注1)
もちろん、ベクトルポテンシャルを使って、 有限要素法等の数値解法で解くといった方法等もあります。 また、実測の場合は、L11 と L22 に加えて、L11, L22 を並列接続した値を測定し、 並列合成インダクタンスの計算を利用して、L12, L21 を求めるのが良いでしょう。
以上の計算を FreeFem++ で実行するためのプログラムを書くと、例えば、次のようになります。
/* 4 芯フラットケーブルによる 2 対伝送のラインパラメータ */
real a1=0.219e-3, a2=0.5e-3, c1=10e-3, c2=5e-3; /* ケーブル寸法 */
real eps=3.1, c0=2.998e8; /* 絶縁体の比誘電率、光速 */
border b1(t=0,2*pi){ x=a1*cos(t)-3*a2;y=a1*sin(t);label=1;};
border b1i(t=0,2*pi){ x=a2*cos(t)-3*a2;y=a2*sin(t);label=6;};
border b2(t=0,2*pi){ x=a1*cos(t)-a2;y=a1*sin(t);label=2;};
border b2i(t=0,2*pi){ x=a2*cos(t)-a2;y=a2*sin(t);label=6;};
border b3(t=0,2*pi){ x=a1*cos(t)+a2;y=a1*sin(t);label=3;};
border b3i(t=0,2*pi){ x=a2*cos(t)+a2;y=a2*sin(t);label=6;};
border b4(t=0,2*pi){ x=a1*cos(t)+3*a2;y=a1*sin(t);label=4;};
border b4i(t=0,2*pi){ x=a2*cos(t)+3*a2;y=a2*sin(t);label=6;};
border b10(t=-c2,c2){ x=c1; y=t;label=5;};
border b11(t=c1,-c1){ x=t; y=c2;label=5;};
border b12(t=c2,-c2){ x=-c1; y=t;label=5;};
border b13(t=-c1,c1){ x=t; y=-c2;label=5;};
int n = 50;
mesh Th = buildmesh(b10(n) + b11(n) + b12(n) + b13(n)
+ b1(-n) + b1i(n) + b2(-n) + b2i(n)
+ b3(-n) + b3i(n) + b4(-n) + b4i(n));
plot(Th,wait=0);
fespace Ph(Th, P0);
fespace Vh(Th, P1);
Vh uh, vh, vx, vy;
Ph reg=region; /* 誘電体境界 */
int r1=reg(c1,c2);
Ph erc = eps*(region!=r1) + 1.0*(region==r1);
/* C11 - 導体 1 と他の全ての導体間のキャパシタンス */
problem laplace1(uh, vh) = int2d(Th) (-erc*(dx(uh)*dx(vh)+dy(uh)*dy(vh)))
+ on(2, 3, 4, 5, uh=0)
+ on(1, uh=1);
laplace1;
real error=0.1;
int i;
for (i=0; i<5; i++) {
Th = adaptmesh(Th, uh, inquire=0, err=error);
error = error*0.5;
laplace1;
};
plot(Th,uh,vh,wait=0);
/* electro static energy */
real u1=0.5*int2d(Th)(erc*(dx(uh)*dx(uh)+dy(uh)*dy(uh)));
real C11=u1*17.707e-12; /* F/m */
cout << "C11 = " << C11 << " F/m" << endl;
erc=1.0; /* 真空中のキャパシタンスを再計算 */
laplace1;
u1=0.5*int2d(Th)(erc*(dx(uh)*dx(uh)+dy(uh)*dy(uh)));
real C10=u1*17.707e-12; /* F/m */
cout << "C10 = " << C10 << " F/m" << endl;
/* C22 - 導体 2 と他の全ての導体間のキャパシタンス */
erc = eps*(region!=r1) + 1.0*(region==r1);
problem laplace2(uh, vh) = int2d(Th) (-erc*(dx(uh)*dx(vh)+dy(uh)*dy(vh)))
+ on(1, 2, 4, 5, uh=0)
+ on(3, uh=1);
laplace2;
error=0.1;
for (i=0; i<5; i++) {
Th = adaptmesh(Th, uh, inquire=0, err=error);
error = error*0.5;
laplace2;
};
plot(Th,uh,vh,wait=0);
/* electro static energy */
u1=0.5*int2d(Th)(erc*(dx(uh)*dx(uh)+dy(uh)*dy(uh)));
real C22=u1*17.707e-12; /* F/m */
cout << "C22 = " << C22 << " F/m" << endl;
erc=1.0; /* 真空中のキャパシタンスを再計算 */
laplace2;
u1=0.5*int2d(Th)(erc*(dx(uh)*dx(uh)+dy(uh)*dy(uh)));
real C20=u1*17.707e-12; /* F/m */
cout << "C20 = " << C20 << " F/m" << endl;
/* C12p - 導体 1, 2 と他の全ての導体とのキャパシタンス */
erc = eps*(region!=r1) + 1.0*(region==r1);
problem laplace12(uh, vh) = int2d(Th) (-erc*(dx(uh)*dx(vh)+dy(uh)*dy(vh)))
+ on(2, 4, 5, uh=0)
+ on(1, 3, uh=1);
laplace12;
error=0.1;
for (i=0; i<5; i++) {
Th = adaptmesh(Th, uh, inquire=0, err=error);
error = error*0.5;
laplace12;
};
plot(Th,uh,vh,wait=0);
/* electro static energy */
u1=0.5*int2d(Th)(erc*(dx(uh)*dx(uh)+dy(uh)*dy(uh)));
real C12p=u1*17.707e-12; /* F/m */
cout << "C12p = " << C12p << " F/m" << endl;
erc=1.0; /* 真空中のキャパシタンスを再計算 */
laplace12;
u1=0.5*int2d(Th)(erc*(dx(uh)*dx(uh)+dy(uh)*dy(uh)));
real C12p0=u1*17.707e-12; /* F/m */
cout << "C12p0 = " << C12p0 << " F/m" << endl;
cout << endl;
real C12 = (C11 + C22 - C12p)*0.5;
real C120 = -(C10 + C20 - C12p0) / 2;
real d = (C10 * C20 - C120 * C120) * c0^2;
real L1 = C20 / d;
real L12 = -C120 / d;
real L2 = C10 / d;
cout << "Line Parameters:" << endl;
cout << "C10 = " << C11 - C12 << " F/m" << endl;
cout << "C12 = " << C12 << " F/m" << endl;
cout << "C20 = " << C22 - C12 << " F/m" << endl;
cout << "L1 = " << L1 << " H/m" << endl;
cout << "L12 = " << L12 << " H/m" << endl;
cout << "L2 = " << L2 << " H/m" << endl;
cout << "k = " << L12 / sqrt(L1*L2) << endl;
cout << endl << "Transmission Matrix:" << endl;
/* [C] */
cout << "C=[" << C11 << " " << -C12 << "; ";
cout << -C12 << " " << C22 << "]" << endl;
/* [L] = [C0]^-1/c0^2 */
cout << "L=[" << L1 << " " << L12 << "; ";
cout << L12 << " " << L2 << "]" << endl;
cout << endl;
開領域の問題ですから、真面目にやると境界要素を使うことになりますが、 高い精度が必要というわけではありませんから、 ここでは、フラットケーブルから少し離れた場所に境界(シールド)を設けました。 なお、x 軸対称ですから、境界定義に手間をかけて、上半分だけを解析すると、 より少ない計算時間で高い精度が得られます。
逆行列等の計算は、octave を使うほうが楽ですが、この場合は簡単なので、 FreeFem++ の中で代数的に行いました。
これを FreeFem++で実行すれば、下記の結果が得られます。
Line Parameters: C10 = 4.30973e-11 F/m C12 = 2.28332e-12 F/m C20 = 6.57007e-11 F/m L1 = 4.52532e-07 H/m L12 = 2.64052e-08 H/m L2 = 3.58025e-07 H/m k = 0.0656007 Transmission Matrix: C=[4.53806e-11 -2.28332e-12; -2.28332e-12 6.7984e-11] L=[4.52532e-07 2.64052e-08; 2.64052e-08 3.58025e-07]
k は Spice の相互インダクタンス素子で必要になる 「結合係数」(coefficient of coupling)で、下記の定義になります。
k = L12 / sqrt(L1*L2)ここで、k の値は、
0 <= k <= 1になることを忘れないでください。
回路定数が得られましたので、以下、1図において、 伝送ラインの長さを 5 m として、
RS1 1 2 50 RS2 3 0 1K RL1 1 2 50 RL2 3 0 1K
の入出力インピーダンスと、立上り時間 2 ns のパルス信号源
VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 50NS 1000NS)を考えることにします。 RS1, RS2, RL1, RL2, VIN の記述は Spice の記法です。
3図の伝送ラインを単一の L1, L2, L12, C10, C20, C12 で近似したのでは、 電磁波が伝送ラインを時間 0 で通過することになって、電圧と電流が伝送ラインの場所によって違うという、 分布定数線路の性格が失われてしまいますから、これら 6 つの素子から構成される、 多数のセグメントに分割しなければなりませんが、波形の立上りを見たい以上、 1セグメントの長さを、 立上り時間に電磁波が進む距離の 1/10 以下にする というのが1つの目安になります。 1/10 の分解能があれば良いだろうという判断です。
伝送ラインの電磁波の位相速度は
v = 1 / sqrt(L*C) ここに、 v = 伝送線路を電磁波が進む速さ (位相速度) (m/s) L = 伝送線路のインダクタンス (H/m) C = 伝送線路のキャパシタンス (F/m)ですから、L1 = 4.5e-7, C10 = 4.5e-11 なら、 v = 2.2e8 m/s (= sqrt(L1*C11) と、 2 ns の立上り時間に進む電磁波の距離は 0.44 m です。つまり、0.044 m 以下に分割しなければなりません。
5 m で 125 セクションと、ちょっと人手で書ける量ではありませんから、 下記のような awk のプログラムで Spice のネットリストを生成します。
#! /bin/sh
/usr/bin/awk '
BEGIN {
n = 25 # 1 m を n 分割
l = 5 # 伝送ラインの長さ
nsec = l * n # セクション数
C10 = 4.30973e-11 / n
C12 = 2.28332e-12 / n
C20 = 6.57007e-11 / n
L1 = 4.52532e-07 / n
L12 = 2.64052e-08 / n
L2 = 3.58025e-07 / n
print "FLAT CABLE CROSSTALK [10/0.12*1.0PVC^4]"
print ".SUBCKT XSECTION N1 N2 F1 F2"
printf "L1 N1 F1 %g\n", L1
printf "L2 N2 F2 %g\n", L2
printf "K1 L1 L2 %g\n", L12 / sqrt(L1*L2)
printf "C1 F1 0 %g\n", C10
printf "C2 F2 0 %g\n", C20
printf "C12 F1 F2 %g\n", C12
print ".ENDS SECTION"
print ""
print "RS1 1 2 50"
print "RS2 3 0 1K"
print "XTLINE0 2 3 101 102 XSECTION"
for (i = 1; i <= nsec; i++) {
j = 2 * i
printf "XTLINE%d %d %d %d %d XSECTION\n", \
i, 100 + j - 1, 100 + j, 100 + j + 1, 100 + j + 2
}
j = 2 * i
printf "XTLINE%d %d %d %d %d XSECTION\n", i, 100 + j -1, 100 + j, 4, 5
print "RL1 4 0 50"
print "RL2 5 0 1K"
print "VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 50NS 1000NS)"
print ".CONTROL"
print "tran 0.1N 100N"
print "plot v(4) v(3) v(5)"
print ".ENDC"
print ".END"
exit 0
}'
このプログラムを実行すると、下記の Spice ネットリストが得られます。
FLAT CABLE CROSSTALK [10.0.12*1.0PVC^4] .SUBCKT XSECTION N1 N2 F1 F2 L1 N1 F1 1.81013e-08 L2 N2 F2 1.4321e-08 K1 L1 L2 0.0656006 C1 F1 0 1.72389e-12 C2 F2 0 2.62803e-12 C12 F1 F2 9.13328e-14 .ENDS SECTION RS1 1 2 50 RS2 3 0 1K XTLINE0 2 3 101 102 XSECTION XTLINE1 101 102 103 104 XSECTION XTLINE2 103 104 105 106 XSECTION XTLINE3 105 106 107 108 XSECTION XTLINE4 107 108 109 110 XSECTION XTLINE5 109 110 111 112 XSECTION XTLINE6 111 112 113 114 XSECTION XTLINE7 113 114 115 116 XSECTION XTLINE8 115 116 117 118 XSECTION XTLINE9 117 118 119 120 XSECTION XTLINE10 119 120 121 122 XSECTION XTLINE11 121 122 123 124 XSECTION XTLINE12 123 124 125 126 XSECTION XTLINE13 125 126 127 128 XSECTION XTLINE14 127 128 129 130 XSECTION XTLINE15 129 130 131 132 XSECTION XTLINE16 131 132 133 134 XSECTION XTLINE17 133 134 135 136 XSECTION XTLINE18 135 136 137 138 XSECTION XTLINE19 137 138 139 140 XSECTION XTLINE20 139 140 141 142 XSECTION XTLINE21 141 142 143 144 XSECTION XTLINE22 143 144 145 146 XSECTION XTLINE23 145 146 147 148 XSECTION XTLINE24 147 148 149 150 XSECTION XTLINE25 149 150 151 152 XSECTION XTLINE26 151 152 153 154 XSECTION XTLINE27 153 154 155 156 XSECTION XTLINE28 155 156 157 158 XSECTION XTLINE29 157 158 159 160 XSECTION XTLINE30 159 160 161 162 XSECTION XTLINE31 161 162 163 164 XSECTION XTLINE32 163 164 165 166 XSECTION XTLINE33 165 166 167 168 XSECTION XTLINE34 167 168 169 170 XSECTION XTLINE35 169 170 171 172 XSECTION XTLINE36 171 172 173 174 XSECTION XTLINE37 173 174 175 176 XSECTION XTLINE38 175 176 177 178 XSECTION XTLINE39 177 178 179 180 XSECTION XTLINE40 179 180 181 182 XSECTION XTLINE41 181 182 183 184 XSECTION XTLINE42 183 184 185 186 XSECTION XTLINE43 185 186 187 188 XSECTION XTLINE44 187 188 189 190 XSECTION XTLINE45 189 190 191 192 XSECTION XTLINE46 191 192 193 194 XSECTION XTLINE47 193 194 195 196 XSECTION XTLINE48 195 196 197 198 XSECTION XTLINE49 197 198 199 200 XSECTION XTLINE50 199 200 201 202 XSECTION XTLINE51 201 202 203 204 XSECTION XTLINE52 203 204 205 206 XSECTION XTLINE53 205 206 207 208 XSECTION XTLINE54 207 208 209 210 XSECTION XTLINE55 209 210 211 212 XSECTION XTLINE56 211 212 213 214 XSECTION XTLINE57 213 214 215 216 XSECTION XTLINE58 215 216 217 218 XSECTION XTLINE59 217 218 219 220 XSECTION XTLINE60 219 220 221 222 XSECTION XTLINE61 221 222 223 224 XSECTION XTLINE62 223 224 225 226 XSECTION XTLINE63 225 226 227 228 XSECTION XTLINE64 227 228 229 230 XSECTION XTLINE65 229 230 231 232 XSECTION XTLINE66 231 232 233 234 XSECTION XTLINE67 233 234 235 236 XSECTION XTLINE68 235 236 237 238 XSECTION XTLINE69 237 238 239 240 XSECTION XTLINE70 239 240 241 242 XSECTION XTLINE71 241 242 243 244 XSECTION XTLINE72 243 244 245 246 XSECTION XTLINE73 245 246 247 248 XSECTION XTLINE74 247 248 249 250 XSECTION XTLINE75 249 250 251 252 XSECTION XTLINE76 251 252 253 254 XSECTION XTLINE77 253 254 255 256 XSECTION XTLINE78 255 256 257 258 XSECTION XTLINE79 257 258 259 260 XSECTION XTLINE80 259 260 261 262 XSECTION XTLINE81 261 262 263 264 XSECTION XTLINE82 263 264 265 266 XSECTION XTLINE83 265 266 267 268 XSECTION XTLINE84 267 268 269 270 XSECTION XTLINE85 269 270 271 272 XSECTION XTLINE86 271 272 273 274 XSECTION XTLINE87 273 274 275 276 XSECTION XTLINE88 275 276 277 278 XSECTION XTLINE89 277 278 279 280 XSECTION XTLINE90 279 280 281 282 XSECTION XTLINE91 281 282 283 284 XSECTION XTLINE92 283 284 285 286 XSECTION XTLINE93 285 286 287 288 XSECTION XTLINE94 287 288 289 290 XSECTION XTLINE95 289 290 291 292 XSECTION XTLINE96 291 292 293 294 XSECTION XTLINE97 293 294 295 296 XSECTION XTLINE98 295 296 297 298 XSECTION XTLINE99 297 298 299 300 XSECTION XTLINE100 299 300 301 302 XSECTION XTLINE101 301 302 303 304 XSECTION XTLINE102 303 304 305 306 XSECTION XTLINE103 305 306 307 308 XSECTION XTLINE104 307 308 309 310 XSECTION XTLINE105 309 310 311 312 XSECTION XTLINE106 311 312 313 314 XSECTION XTLINE107 313 314 315 316 XSECTION XTLINE108 315 316 317 318 XSECTION XTLINE109 317 318 319 320 XSECTION XTLINE110 319 320 321 322 XSECTION XTLINE111 321 322 323 324 XSECTION XTLINE112 323 324 325 326 XSECTION XTLINE113 325 326 327 328 XSECTION XTLINE114 327 328 329 330 XSECTION XTLINE115 329 330 331 332 XSECTION XTLINE116 331 332 333 334 XSECTION XTLINE117 333 334 335 336 XSECTION XTLINE118 335 336 337 338 XSECTION XTLINE119 337 338 339 340 XSECTION XTLINE120 339 340 341 342 XSECTION XTLINE121 341 342 343 344 XSECTION XTLINE122 343 344 345 346 XSECTION XTLINE123 345 346 347 348 XSECTION XTLINE124 347 348 349 350 XSECTION XTLINE125 349 350 351 352 XSECTION XTLINE126 351 352 4 5 XSECTION RL1 4 0 50 RL2 5 0 1K VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 50NS 1000NS) .CONTROL tran 0.1N 100N plot v(4) v(3) v(5) .ENDC .END
この多量の計算を長い時間をかけて実行すると、下記のようになります。 v(3) が NEXT (Near-End Cross-Talk - 近端漏話)、 v(5) が FEXT (Far-End Cross-Talk - 遠端漏話)、 v(4) が終端の伝送波形になります。 3, 4, 5 は、それぞれ、 1図のノード番号に対応しています。
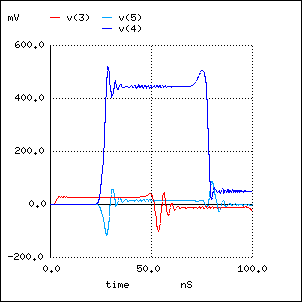
プリント基板とか、短いケーブルですと、区分モデルも役にたちますが、 この状況では少し無理があって、 大体の様子は分かるものの、 離散化に起因するリンギング(振動)と、 それに付随する大きな誤差が出ます。
このような、 区分モデルの欠点は、3図の L12 と C12 という結合素子にあって、 これがなければ、 Spice の伝送線路モデルである、 T (Lossless Transmission Lines)、 ないしは、O (Lossy Transmission Lines) モデルが使えるのですが、 「モード分解」(Modal Decomposition) とよばれる手法で、この結合をなくすことができます! つまり、 1図のノード 2, 3, 4, 5 から見る限り、まったく同じに見えて、しかも、 L12 と C12 を含まない、 独立した2つの回路に変換することができるのです。
以下、前記と同様に、損失 R, G が無視できて、 相互インダクタンスと相互キャパシタンスを含む、 複数の伝送ラインを考えますが、 R, G が無視できない場合でも、より複雑にはなりますが、同じように扱えます。
まず、すべての伝送ライン上の電圧と電流をベクトルにまとめて、
[V] = [V1; V2; .. Vn] [I] = [I1; I2; .. In] ここに、 Vi = 伝送回路 1 のある点に於ける電圧 (i = 1, 2, .. n) Ii = 伝送回路 1 のある点に於ける電流 (i = 1, 2, .. n)とすれば、伝送ライン上の電圧と電流の間には、下記の関係があります。
(d/dz)([V]) = -[L]*(d/dt)([I]) (d/dz)([I]) = -[C]*(d/dt)([V]) [L] = [L11, L12, .. L1n; L21, L22, .. L2n; .. Ln1, Ln2, .. Lnn] [C] = [C11, C12, .. C1n; C21, C22, .. C2n; .. Cn1, Cn2, .. Cnn] ここに、 Lii = 回路 i の自己インダクタンス (i = 1, 2, .. n) Lij (i!=j) = 回路 i と回路 j の相互インダクタンス (i, j = 1, 2, .. n) Cii = 回路 i のキャパシタンス (i = 1, 2, .. n) Lij (i!=j) = 回路 i と回路 j の相互キャパシタンス (i, j = 1, 2, .. n) j = sqrt(-1) ω = 2*π*f π = 3.14159265.. f = 周波数 (Hz) (d/dz)(x) = x の伝送方向の偏微分 (d/dt)(x) = x の時間微分
ここで、下記のように変換すると、 [L] と[C] が、それぞれ、[l] と [c] に 対角化できて、 結合のない独立した2つの回路に分離(decomposition) することができます。(注2)
[l] = inv(M)*[L]*[N] [c] = inv(N)*[C]*[M] [v] = [M]*[V] [i] = inv([N])*[I] inv([N]) = [M]' [z0] = sqrt([l]*inv(c)) [s] = 1 / sqrt([l]*[c]) ここに、 [M] = [L]*[C] の固有マトリクス [N] = [C]*[L] の固有マトリクス [M]' = [M] の転置行列 [l] = モード領域のインダクタンス (H/m) [c] = モード領域のキャパシタンス (F/m) [v] = モード領域の電圧 (V) [i] = モード領域の電流 (A) [z0] = モード領域の特性インピーダンス (Ohm) [s] = モード領域の位相速度 (m/s)
この変換で、[l] と [c] が対角行列になる のがポイントですが、この対角化した [l], [c] と、それに対応する、 [v], [i] の世界を 「モード領域」(modal domain)と呼び、 もとの [L], [C], [V], [I] の世界を 「実領域」(actual domain)と呼びます。
モード領域の電圧と電流は実領域とは違いますが、電力が保存され、抵抗、 インダクタンス、キャパシタンス、特性インピーダンス、 伝搬定数といった回路の概念が実領域と同じように使えますので、 他の回路とのやっかいな結合なしの、 独立した伝送ラインとして扱うことができ、 計算が極めて簡単になります。 つまり、相互に関連した 連立方程式を独立した方程式の集合に転化できるわけです。 これで「各個撃破」という、楽な戦術が使えるようになります。
なお、 モード領域の電圧と電流は、回路間の電圧比と電流比だけが意味を持ち、 個々の絶対値には物理的な意味がないのですが、このあいまいさ(自由度)は、 モード領域への変換と、その逆変換で打ち消されますので、 以下の計算では、考えなくて済みます。
さて、モード領域と実領域の電圧電流関係を Spice で扱うには、 いくつかの方法がありますが、
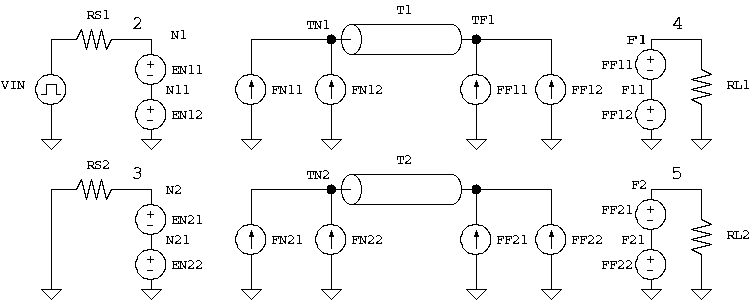
4図 モード分解を利用した等価回路
モード空間の伝送ライン T1 と T2 の特性インピーダンスと伝搬定数は、[l], [c] から計算しますが、 この場合は、次のようになります。
Z01 = sqrt(l11 / c11) Z02 = sqrt(l22 / c22) v1 = 1 / (sqrt(l11 * c11)) v2 = 1 / (sqrt(l22 * c22)) ここに、 Z01 = 伝送線路 T1 のモード領域の特性インピーダンス Z02 = 伝送線路 T2 のモード領域の特性インピーダンス v1 = 伝送線路 T1 のモード領域の位相速度 v2 = 伝送線路 T2 のモード領域の位相速度
この等価回路のネットリストを生成するプログラムを octave で書けば、 例えば、次のようになります。 Spice の伝送線路には簡単な T モデルを使っていますので、 線路特性は、特性インピーダンス Z0= と、 位相速度と線路の長さを1つにまとめた、 遅延時間 TD= で指定することになります。
#! /bin/sh
# FLAT CABLE CROSSTALK [10.0.12*1.0PVC^4]
/usr/local/bin/octave -q <<!
C=[4.53653e-11 -2.27549e-12; -2.27549e-12 6.80798e-11];
L=[4.52517e-07 2.6381e-08; 2.6381e-08 3.58076e-07];
[M,D]=eig(L*C);
Mv=M;
[N,D]=eig(C*L);
Mi=inv(N);
l=inv(M)*L*N;
c=inv(N)*C*M;
z=sqrt(l*inv(c));
t=sqrt(l*c);
printf("FLAT CABLE CROSSTALK [10.0.12*1.0PVC^4]\n");
printf("RS1 1 2 50\n");
printf("RS2 3 0 1K\n");
printf("XT1 2 3 4 5 TLINE\n");
printf("RL1 4 0 50\n");
printf("RL2 5 0 1K\n");
printf("VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 50NS 1000NS)\n");
printf(".SUBCKT TLINE N1 N2 F1 F2\n");
printf("EN11 N1 N11 TN1 0 %7.4f\n", Mv(1,1));
printf("EN12 N11 0 TN2 0 %7.4f\n", Mv(1,2));
printf("EN21 N2 N21 TN1 0 %7.4f\n", Mv(2,1));
printf("EN22 N21 0 TN2 0 %7.4f\n", Mv(2,2));
printf("FN11 0 TN1 EN11 %7.4f\n", Mi(1,1));
printf("FN12 0 TN1 EN21 %7.4f\n", Mi(1,2));
printf("FN21 0 TN2 EN12 %7.4f\n", Mi(2,1));
printf("FN22 0 TN2 EN22 %7.4f\n", Mi(2,2));
printf("T1 TN1 0 TF1 0 TD=%.1fNS Z0=%.1f\n", t(1,1)*1.8*1e9, z(1,1));
printf("T2 TN2 0 TF2 0 TD=%.1fNS Z0=%.1f\n", t(2,2)*1.8*1e9, z(2,2));
printf("EF11 F1 F11 TF1 0 %7.4f\n", Mv(1,1));
printf("EF12 F11 0 TF2 0 %7.4f\n", Mv(1,2));
printf("EF21 F2 F21 TF1 0 %7.4f\n", Mv(2,1));
printf("EF22 F21 0 TF2 0 %7.4f\n", Mv(2,2));
printf("FF11 0 TF1 EF11 %7.4f\n", Mi(1,1));
printf("FF12 0 TF1 EF21 %7.4f\n", Mi(1,2));
printf("FF21 0 TF2 EF12 %7.4f\n", Mi(2,1));
printf("FF22 0 TF2 EF22 %7.4f\n", Mi(2,2));
printf(".ENDS TLINE\n");
printf(".CONTROL\n");
printf("tran 0 100N\n");
printf("plot v(4) v(3) v(5)\n");
printf(".ENDC\n");
printf(".END\n");
!
これを実行すると、次のネットリストが得られます。
FLAT CABLE CROSSTALK [10.0.12*1.0PVC^4] RS1 1 2 50 RS2 3 0 1K XT1 2 3 4 5 TLINE RL1 4 0 50 RL2 5 0 1K VIN 1 0 PULSE(0V 1V 2NS 2NS 2NS 50NS 1000NS) .SUBCKT TLINE N1 N2 F1 F2 EN11 N1 N11 TN1 0 0.1917 EN12 N11 0 TN2 0 -0.9953 EN21 N2 N21 TN1 0 0.9815 EN22 N21 0 TN2 0 0.0969 FN11 0 TN1 EN11 0.1926 FN12 0 TN1 EN21 0.9860 FN21 0 TN2 EN12 -0.9999 FN22 0 TN2 EN22 0.0973 T1 TN1 0 TF1 0 TD=8.9NS Z0=74.1 T2 TN2 0 TF2 0 TD=8.1NS Z0=97.7 EF11 F1 F11 TF1 0 0.1917 EF12 F11 0 TF2 0 -0.9953 EF21 F2 F21 TF1 0 0.9815 EF22 F21 0 TF2 0 0.0969 FF11 0 TF1 EF11 0.1926 FF12 0 TF1 EF21 0.9860 FF21 0 TF2 EF12 -0.9999 FF22 0 TF2 EF22 0.0973 .ENDS TLINE .CONTROL tran 0 100N plot v(4) v(3) v(5) .ENDC .END
この、計算結果は次のとおりですが、区分モデルに比べて、計算時間が極めて少なく、 リンギングの発生もなくなって、反射波の影響がよくわかります。 また、パルス発生器とオシロスコープで実測すると、 同じ結果が得られます。
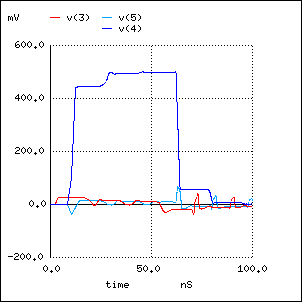
区分モデルのときと同じように、 v(3) が NEXT (Near-End Cross-Talk - 近端漏話)、 v(5) が FEXT (Far-End Cross-Talk - 遠端漏話)、 v(4) が終端の伝送波形になります。 3, 4, 5 は、それぞれ、1図のノード番号に対応しています。
以上、2回路のクロストークを Spice で解析する方法を述べましたが、 3回路以上の場合も、ベクトル [V] と [I]、そして、 行列 [L] と [C] の要素数が増えて、4図の等価回路で、 直列の「電圧制御電圧源」と並列の「電流制御電流源」の個数が増えるだけですから、 まったく同じ手法が使えます。
例えば、L, C (無損失)線路の偏微分方程式
(d/dz)(v) = -L*(d/dt)(i) (d/dz)(i) = -C*(d/dt)(v) ここに、 v = 線路の電圧 i = 線路の電流 (d/dt)(x) = x の時間微分 (d/dz)(x) = x の線路長さ方向(z)の偏微分で、進行波
v(z,t) = V*f(z - c*t) i(z,t) = I*f(z - c*t) ここに、 c = 進行波の速度 (誘電体が真空なら、c は光速)を考えると、後の2式をその直前の2式に代入して得られる、
V = c*L*I I = c*C*Vから、
L = 1 / (C * c^2)がわかります。
この分野の論文が数多く生まれた 1970 年代と違って、 最近は、解説書も多いのですが、 多線条線路のモード解析 (Modal Analysis) については、 例えば、下記をご覧ください。
J.A.Brandao Faria,- Multiconducor Transmission-Line Structures: Modal Analysis Techniques (John Wiley & Sons Inc) ISBN 0-471-57443-0
固有値と固有ベクトルを使って、問題を単純化する手法は、古くから、機械振動、 送配電回路解析を含む、広い分野で使われています。 行列の固有値論は、実り多い分野の1つで、大学の線形代数のコースも、 もう少しスリルに満ちたものにできないかと思うのですが、 不勉強だった私も悪いかもしれません。
なお、モード分解と Spice を組み合わせた、前記の手法は、例えば、
VIJAI K.TRIPATH, JOHN B.RETTIG,- A SPICE Model for Multiple Coupled Microstrips and Other Transmission Lines, IEEE Transaction on Microwave Theory and Techniques, Vol. MTT-33, No.12, December 1985等、たくさんあります。
数値解法では本質的に、ポテンシャル誤差に比べてエネルギ誤差が格段に少ないため、 回路定数を求める場合は、エネルギを使うのが原則です。 エネルギから求めたインピーダンス、損失といった値は、 ポテンシャル解に本質的な誤差が含まれていても、驚く程高い精度が得られます。
この問題については、例えば、
Peter P.Silvester and Ronald L.Ferrari,- Finit elements for electrical engineers (Third Edition) (Cambridge University Press) ISBN0-521-44505-1の 41 ページをご覧ください。
平林 浩一, 2004