伝送線路の SPICE モデル

電気回路シミュレータSPICEには無損失伝送線路(Lossless Transmission Lines)Tモデルの他、 RLC/RC/RG 素子を考慮した有損失伝送線路(Lossy Transmission Lines) Oモデルがあるのですが、 抵抗 R の周波数特性を考慮していないため、 集積回路や小さな印刷基板の解析では使えても、 長いケーブル伝送では使えません。

そこで、無限個の電気回路素子 R, L, C, G から構成されている伝送線路を有限個の素子で近似する 等価回路を求めることを考えます。(注１)

この等価回路は SPICE などの回路シミュレータで伝送線路の過渡解析をしたり、 大域的周波数特性を求めたり、イコライザ回路を考えたり、 ケーブルの電気的メカニズムの理解に役立ちます。

1. 伝搬遅延

高周波に於ける伝送線路の電気特性は

1. 速度係数と長さで決まる(無歪)伝搬遅延
2. 導体の表皮効果で決まる (周波数の平方根に比例する)減衰と位相歪

  Vr = 1 / sqrt(L * C)                                  (1)
     = 1 / sqrt(εs)                                    (2)
ここに、
	Vr = 速度係数 (0 < Vr <= 1)
	L = 同軸ケーブルの外部インダクタンス (H/m)
	C = 同軸ケーブルのキャパシタンス (F/m)
	l = 同軸ケーブルの長さ (m)
	εs = 誘電体の比誘電率 (ポリエチレン絶縁なら 2.3)

  TD = l / (c * Vr)                                     (3)
  ここに、
	TD = 遅延時間 (s)
	c = 真空中の光速 (2.99792458 m/s)
	Vr = 速度係数

2. 減衰と位相歪

一方、 減衰と位相歪は導体の渦電流損失(eddy current loss)で決まるため面倒です。 ただ、 渦電流損失のほとんどは導体の表皮効果(skin effect)によるものですから、 まず、同軸ケーブルの中心導体のような単独円筒導体を考えます。

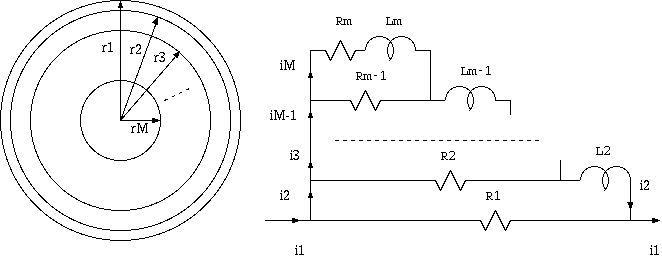
同軸ケーブル中心導体の電磁場は中心軸に対象ですから、 １図のように同心円筒に分割する離散化が素直です。 (注２)

Ri は外半径 r(i) の円筒(最内層だけは円柱)の直流抵抗、 Lm はその円筒を流れる電流による(その円筒の)一つ外側の円筒内部に生まれた磁束 に起因する自己インダクタンスです。 最外層の電流による磁束は導体外部になって、 (無歪)伝搬遅延の原因となりますので、 導体内部モデルには入れる必要がなくなって、R1 のみになります。

１図 同軸ケーブル中心導体の離散化

同心円の半径をいかに選ぶかが問題ですが、 周波数が高くなるにつれて電流が表面に集中しますから、 外周に近付くほど細かく分割するほうが有利で、

  Ri+1 / Ri = N                                     (4)
  ここに、
	Ri = 外周から i 番目の円筒の直流抵抗
	Ri+1 = 外周から i+1 番目の円筒の直流抵抗
	N = 定数

この方針だと、 １図の等価回路のパラメータは下記のアルゴリズムで決定することができます。 (注４)

  R(1) = Rdc * (N^M - 1) / (N - 1)                    (5)
  R(i+1) = R(i) * N                                   (6)
  L(i) = μ * (r(i-1) - r(i)) / (2 * π * r(i))       (7)
  r(1) = a                                            (8)
  r(i) = r(i-1) - 1 / (σ * π * R(i-1))              (9)
  Rdc = 1 / (σ * π * a^2)                          (10)
  ここに、
	i = 1, 2, .. M
	R(1) = 最外層円筒の直流抵抗 (Ω/m)
	R(i) = 外から i 番目の直流抵抗 (Ω/m)
	R(i+1) = 外から i + 1 番目の直流抵抗 (Ω/m)
	r(1) = a = 導体半径 (m)
	r(i) = 外から i 番目の円筒外径 (m)
	r(i+1) = 外から i+1 番目の円筒外径 (m)
	Rdc = 導体の直流抵抗 (Ω)
	σ = 導電率 (S/m)
	σ = 導電率 (S/m)
	μ = 透磁率 (H/m)
	π = 3.1415 ..

一方、M はこのモデルの適用可能な周波数上限を決めることになります。 この上限は最外周円筒の厚さが侵入深さ(skin depth)の 3 倍程になる周波数 ですから、 これをモデルの適用限界とすると、下記の関係が得られます。 (注５)

  fmax = 9 / Rdc / μ / (1 - sqrt(1 - (N - 1) / (N^M - 1)))^2      (11)
  ここに、
	fmax = このモデルの適用可能上限周波数 (Hz)

  M = log(1 + (N - 1) / (1 - (1 - 3 * sqrt(Rdc / (μ * fmax)))^2) / log(N)    (12)

3. 一般の伝送線路

周波数が高くなると表皮効果(skin effect)により、 電流は導体表面にしか存在しなくなりますから、 導体の高周波抵抗、すなわち減衰定数は 導体の表皮抵抗と導体表面の周長だけで決まり、 下記の関係が成立ちます。 (注５)

  α = Rs / (4 * π * a * Z0)
  ここに、
	α = 減衰定数 (neper/m)
	a = 導体半径 (m)
	Rs = 導体の表面抵抗 (Ω*m)
	   = 1/(σ*δ)
	   = sqrt(ω*μ/(2*σ)
	σ = 導電率 (S/m)
	σ = 導電率 (S/m)
	μ = 透磁率(H/m)
	δ = 表皮深さ (m)
	   = sqrt(2/(ω*μ*σ)
	Z0 = 特性インピーダンス (Ω)

例えば、 往復平行導体(twin lead)の場合は二つの導体の損失が同じですから、 比較的小さい近接効果(proximity effect)を無視すれば、 導体径を 1/2 にした同軸ケーブル内部導体の損失と同じです。 (注６)

同軸ケーブル(coaxial cable)の場合は

  α = Rhf / (2 * Z0)
  Rhf = Rs / (2 * π) * (1 / a + 1 / b)
  Z0 = 60 / sqrt(εs) * log(b / a)
  ここに、
	α = 減衰定数 (neper/m)
	Rhf = 導体の高周波抵抗 (Ω)
	a = 内部導体半径 (m)
	b = 外部導体半径 (m)
	Z0 = 特性インピーダンス (Ω)
	εs = 絶縁体の比誘電率 (ポリエチレンで 2.3)

  a * b / (a + b)

ストリップライン(strip line)の場合は、 近接効果により電流は平版導体の向かい合った面だけに存在しますから、 電流が端部で増加するedge effectを無視すれば、 導体半径が

  導体幅 / (2 * π)

つまり、 任意の高周波伝送線路は同じ減衰を持つ同軸ケーブル内部導体に変換できますから、 現実の伝送線路と同じ減衰を持つ単独円筒導体の半径を求めて、 この等価半径で前記の表皮効果モデルを作り、 現実の伝送線路の特性インピーダンスと速度係数を持つ無歪遅延回路をつなげば、 現実に近い伝送波形を再現する伝送線路モデルを作ることができます。

この等価半径は下記の(伝送線路の基本的)関係から簡単に得られます。 (注７)

  Rhf = Rs / (2 * π * a)                              (13)
  α = Rhf / (2 * Z0)                                  (14)
  ここに、
	Rhf = 伝送線路の高周波抵抗 (Ω/m)
	Rs = 導体の表面抵抗 (注５参照)
	a = 等価導体半径 (m)
	α = 伝送線路の減衰定数 (Neper/m)
	Z0 = 伝送線路の特性インピーダンス (Ω)

  a = sqrt(f / (π * σ)) / (4 * Z0 * α)            (15)

  α = sqrt(f * μ * Rdc) / (4 * Z0)                 (16)

なお、(16) で Rdc と Z0 だけで減衰が決まる点に注意してください。 Z0 が大きくなると減衰が減るのは導体電流の起源となる電界のエネルギが 磁界のエネルギに移動するためです。 つまり、空間に存在するエネルギが増加します。

このSPICE モデルを生成するプログラムの一例を awk scriptとして付けておきます。

注

注 1. 伝送線路の回路モデル

伝送線路を下記の微小回路の長さ方向積分として表現したのは 孤高の天才 Heaviside ですが、 高周波では、この回路の抵抗 R と L が大きな周波数特性を持つため、 解析解を求めることができません。 これを数値計算で扱えるようにしようというのが、 この解説の目的です。

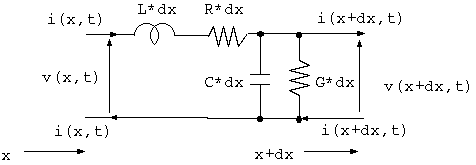
x.１図 - 伝送線路の回路表現

金属導体の高周波抵抗が周波数の平方根に比例して増加するのは 導体中の Maxwell 方程式に起因する宿命で、 これが高周波ケーブルの高周波特性に反映します。

注 2. １図の等価回路の起源

この等価回路のアイデアは下記によります。

  H.A.Wheeler, Fourmulas for the skin effect
	Proc. IRE, vol. 30, pp. 412-424, Sept. 1942

注 3. 円筒の分割方針

この分割方法のアイデアは下記によります。

Chu-Sun Yen, Zvonko Fazarinc and Richard wheeler,-
Time-Domain Skin-Effect Model for Transient Analysis of Lossy Transmission Lines
(Proc. IEEEE, Vol. 7, Jul. 1982, pp 750-757

注 4. 離散化パラメータの決定

１図に於いて、 導電率が十分高く変移電流が無視できて、 電流が電界と導電率の積で表現できる導体中の Maxwell 方程式

  rot J = -μ * σ * ∂H / ∂t     (4.1)
  rot H = J                        (4.2)
  ここに、
	J = 導体内部の電流密度 (A/m^2)
	H = 導体内部の磁界 (amp-turn/m)
	σ = 導体の導電率 (S/m)
	σ = 導体の導電率 (S/m)
	μ = 導体の透磁率 (H/m)

  I(r, t) = 2 * π * r * H(r, t)                     (4.3)
  ここに、
	I(r, t) = 半径 r の内側の電流
	H(t, t) = 半径 r の磁界

  ∂J(r,t)/∂t = (μ*σ/(2*π*r))*∂I(r,t)/∂t        (4.4)

  J(i-1)/(r(i-1)-r(i)) = (μ*σ/(2*π*r(i))*dI(i)/dt  (4.5)
  J(j) = (I(i) - I(i+1)/A(i)                          (4.6)
  ここに、
	A(i) = i 番目の円筒の面積

  Ri = i 番目の円筒の抵抗
     = 1 / (σ * A(i))
  Li = i 番目の円筒の内部インダクタンス
     = μ * (r(i-1) - r(i)) / (2 * π * r(i))

  R(i-1)*(I(i-1)-I(i)) - Ri*(I(i) - I(i+1)) = Li*dI(i)/dt     (4.7)

注 5. 侵入の深さ

導体中の電磁波は導体表面から内部に進むに従って指数的に減衰しiながら 位相も遅れてゆきますが、 この減衰の程度を表す指標が下記の侵入の深さ(Skin depth)です。

  δ = sqrt(2 / (ω * μ * σ))
  ここに、
	δ = 侵入の深さ (m)
	ω = 角周波数 (rad/s)
	   = 2 * π * f
	f = 周波数 (Hz)

上限周波数 fmax は

  r2^2 = r1^2 - 1 / (σ * π * R1) = r1^2 * (1 - (N - 1) / (N^M - 1))

  r1 - r2 = 3 * δ

なお、導体の厚さが 3 * δ より厚い場合、 下記の表面抵抗(surface resistance)の概念を使うと、 導体の高周波に於けるインピーダンスを極めて容易に計算することができます。

  Zs = Rs + j * Xs = (1 + j) / (δ * σ)
     = Rs * (i + j)
  ここに、
	Rs = 表面抵抗 (Ω * m^2)
	   = sqrt(ω * μ / (2 * σ))

ここで、Rs と Xs の値が等しいことに注意してください。 パルス伝送波形の歪は減衰でなく位相歪で決まりますが、 位相歪の原因となるリアクタンス分 Xs は減衰を決める Rs と同じ大きさなので、 見掛け上減衰がパルス波形の歪を決めるようにも見えてしまいます。 単純な減衰だけでは、ケーブルの伝送波形は説明できません。 R-C, R-L 回路の波形は指数関数、ケーブルの伝送波形は誤差関数ですから、 同じメカニズムではないのです。

なお、上記の表皮抵抗を使うと円筒導体の高周波に於ける交流抵抗と直流抵抗の比は

  Rac / Rdc = sqrt(μ) / 2 * sqrt(f / Rdc)

注 6. 平行線の近接効果

例えば、平行線の場合は往復導体の表皮効果に加えて、 電流分布が平行線の内側に偏り、 これを近接効果(Proximitu effect)と呼んでいますが、 a / δ > 100 が成り立つ高周波の場合、 この近接効果による交流抵抗の増加は下記の値になることが証明できます。

  Phf = 1 / sqrt(1 - 1 / (s / (2 * a))^2)
  ここに、
	Phf = 導体の高周波抵抗 / 表皮効果のみ考慮した導体の高周波抵抗
	a = 導体半径 (m)
	s = 導体中心間距離 (m)

注 7. 伝送線路の減衰