信号処理系(signal processing system)の部品に 機械的衝撃や振動を与えたとき発生するノイズを microphonics(マイクロフォニックス)とか microphonic noise(マイクロフォニック雑音)と呼びますが、 電線の場合は、電線から見た負荷インピーダンスが 10 kOhm 以上で、 mV オーダーの低電圧を扱うときに問題になることが多いようです。
例えば、PH メータ電極のリード線などの 高インピーダンスセンサのリード線、 高インピーダンスマイクロホンのコード、 電気ギターのコード等が典型的な例で、 電線を動かしたり、衝撃を与えたりすると、音として聞いたとき、 ジャリジャリとか、シャリシャリ、ポンポン、ドンドンといったノイズが出ます。
後でわかるように、このノイズ源は本質的に定電流特性になるため、 負荷インピーダンスが低い場合は問題になりません。
電線のマイクロフォニックスの原因のほとんどは、 静電気(static electricity)によるものですが、 以下、その基本的なメカニズムを考えてみます。
Platoがコハクと毛皮の摩擦に起因する毛髪や小片の吸引現象を、 その著作(Timaeus)に記述したのが起源前四世紀ということで、 静電気問題の歴史は長いのですが、その複雑で多様な機構故に、 今なお未知の問題が、たくさんあります。
ここでは、固体表面の物理という根本的な問題には触れずに、 電線のマイクロフォニックスを理解するために最低限必要な話題に限定して 考えることにします。
まず、静電気現象は次ぎの3つの過程から構成されています。
電荷移動 -> 電荷分離 -> 電荷暖和
異種の固体同士を接触されると、いろいろな原因で、 一方の物質から他方の物質へと電荷移動が起きます。 この段階では、電気2重層ができるだけですから、 外部に対する影響は、ほとんど、ありません。
いろいろな原因というのは、エネルギ順位の差、熱起電力、拡散、 電解質の起電力によるイオンの移動、表面の剥離移転など、たくさんあるのですが、 金属同士の接触ならフェルミ準位が等しくなるように、電子が移動しますから、 移動する電荷の量は、 仕事関数(物質内の電子を表面から取り出すのに必要なエネルギ)の差に 比例することになります。
金属と絶縁体の接触の場合は、かなり複雑ですが、 絶縁体に対する表面準位を考えることで、 金属と同様に扱えるという研究が、いろいろあります。 そのため、電荷がどの程度どの方向に分離するかは、 組み合わせる物質によってほぼ決まっていて、この関係を表す方法として、 1753 年にWilckeにより、 帯電列(注1)が提案されました。 これは、1列に並べられた物質群から任意の2物質を取り出すと、 上側の物質が正、下側の物質が負に帯電するというものです。 もちろん、電荷分離は物質本来の物性以外に、 その物質の表面状態(注2)に依存しますから、 こういった表ですべてが表現できるわけではないのですが、 その後も、いろいろな系列が発表されています。
次ぎに、接触した2つの物体が離れると、分離した電荷の一部が残留し、 静電気が発生します。この、電荷分離過程では、
Q = C * V ここに、 Q = (分離した)電荷 (C) C = (2つの荷電物体間の)キャパシタンス (F) V = (2つの電荷間の)電位差 (V)ですから、荷電物体が離れるに従って、キャパシタンスが減少する結果、 電位差が増大し、 高電圧による 電撃や放電による爆発とか火災の原因となるわけです。
放電以外にも、分離した正負の電荷の間に導電路があれば、 いずれ電荷は消滅するわけですが、これが電荷暖和過程になります。
以下、電線に於ける静電気の電荷移動、電荷分離、電荷暖和過程を考えます。
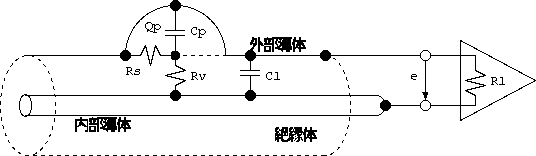
電線で固体間の接触と分離が一番起きやすいのは、 同軸ケーブルないしシールド線の外部導体と絶縁体表面の間ですから、 1図のモデルを考えます。 機械的変形と共に、Cp, Rs が変化しますから、回路定数が時間とともに変化しますが、 放電(電荷暖和)時間が機械的変形速度より短ければ、かなり良い近似になりますし、 放電時間が機械的変形速度より長ければ、また電気2重層に戻って、 大きなノイズ源にはなりません。

1図 マイクロフォニックスの発生機構
ここで、
Qp = 外部導体の一部が絶縁体表面から離れてたとき分離する電荷 (C) Cp = その部分のキャパシタンス (F) Rv = 絶縁体表面の電荷から内部導体までの(絶縁)抵抗 (Ohm) Rs = 絶縁体表面の電荷から外部導体までの表面抵抗 (Ohm) Cl = 外部導体と内部導体のキャパシタンス (F) Rl = 負荷抵抗 (Ohm)です。
この回路で、電荷 Q0 が放電するとき、負荷抵抗 Rl に、 どんなノイズが発生するかを調べるために、1図を書き換えた2図の回路で、 C1 の電荷 Q1 の初期値を 0、Cp の電荷の初期値を Qp として、 R1 の電圧 e を求めると、下記の結果が得られます。(注3)
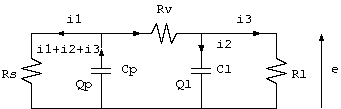
2図 分離した電荷 Qp の放電経路
e = (2*Qp*Rl*Rs*exp(-β*t)*sinh(γ*t)) /sqrt((Cp*Rv*Rs+Cl*Rv*Rl+Cp*Rl*Rs+Cl*Rl*Rs)^2 -4*Cp*Cl*Rv*Rl*Rs*(Rv+Rl+Rs)) (1) ここに、 β = (1/CP/Rl+1/Cl/Rv+1/Cp/Rs+1/Cp/Rv)/2 γ = sqrt((β^2-4/Cp/Cl*(1/Rl/RS+1/Rv/Rs+1/Rv/Rl))/2
(1) 式は比例定数を除いて、sinh(γ*t) と exp(-β*t) の積ですが、 sinh(γ*t) は t = 0 から、最初のうちは時間に比例して増加し、 時間の経過と共に加速度的に増加して無限大になる関数、 exp(-β*t) は時間に経過と共に加速度的に減少して 0 に近付く関数です。 一方、物理的に見て、長い時間経てば e = 0 になるのは明らかですから、 t = 0 から立ち上がって、極大に達し、その後減衰するという 衝撃波になることが予想できます。
今、(1) 式の波形が直観的にわかるように、 特定のケースについてSpiceで計算した結果は、3図のようになります。 (注4)
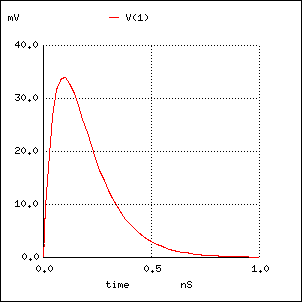
3図 2図の回路の e の波形例
これを見ると、電線が衝撃波発生器になるということが、よくわかります。 もちろん、L, C を使った衝撃波発生器に比べて、効率は悪いですから、 衝撃波発生装置として、こんな回路を使うことはないでしょう。
ここで、最も興味があるのは、最大電圧の値と時刻ですが、 下記のようになります。
max(e) = Qp*f(a)*sqrt(Rl*Rs/(Cp*Cl*(Rv+Rl+Rs)) (2) t0 = arccoth(β/γ) (3) f(a) = exp(-tanh(sqrt(1-a))/sqrt(1-a) a = 4*Cp*Cl*Rv*Rl*Rs*(Rv+Rl+Rs) /(Cp*Rv*Rs+Cp*Rl*Rs+Cl*Rv*Rl+Cl*Rl*Rs)^2 (4) ここに、 max(e) = e の極大値 (V) t0 = e が極大になる時間 (sec)
(4) 式が無次元数になることと、a が単調増加関数で、 0 <= a < 1 になることに注意してください。 また、(2), (3), (4) のほとんどが Rv で規格化できますから、 Rv が重要な基準になります。
波高値が最大になるのは、Rl が無限大になったときですが、 (1) 式は依然として衝撃波の形を保っていて、 立ち上がりが急速になり、 立ち下がりが遅くなります。 この場合は、
max(max(e)) = Qp*f(a0)*sqrt(Rs/Cp/Cl) (5) a0 = 4*Cv*Cl*Rv*Rs/(Cp*Rs+Cl*Rs+Cl*Rs)^2 (6)で、この値を測定すれば、電線のマイクロフォニックスのおよその評価ができます。
電線が受ける機械的衝撃はいろいろですから、 常に、(1) 式の波形になるとは限りませんが、 実際に実験して得られる典型的な波形は3図のようなもので、 このモデルが実態に近いと考えて良さそうです。
MOS-FET 等で高い負荷インピーダンスを作って、実験すれば、 数 V に達する、長時間の衝撃波形が得られますので、 安価なオシロスコープでも、容易に確認することができます。
マイクロフォニック対策が行われた電線は、いろいろな手法の組み合わせで、 この値が小さくなるように設計されています。
帯電は、物体の表面状態や、摩擦等の接触の仕方で、かなり変化しますので、 実験結果も細部では一致しません。 一番左の列は金属の仕事関数順です。
| (+) | (+) | (+) | (+) | (+) | (+) | (+) | (+) | (+) | (+) | (+) | |
| アスベスト | アスベスト | ||||||||||
| 猫毛皮 | 人毛 | ||||||||||
| 磨いたガラス | ガラス | ガラス | ガラス | ガラス | ガラス | ||||||
| 人毛 | 頭髪 | ||||||||||
| 雲母 | 雲母 | 雲母 | |||||||||
| ナイロン糸 | |||||||||||
| 猫毛皮 | ナイロンポリマ | ナイロン | |||||||||
| 羊毛 | 羊毛 | 羊毛 | 羊毛 | 羊毛 | 羊毛 | 羊毛 | 羊毛 | 羊毛 | |||
| 猫毛皮 | ナイロン | ナイロン | |||||||||
| Pb | ペン用の羽 | ペン用の羽 | 羽 | 鉛 | ビスコース | レーヨン | |||||
| フリントガラス | 木綿 | エチルセルロース | |||||||||
| 綿 | 絹 | 絹 | 絹 | 絹 | 絹 | 絹布 | |||||
| 麻 | ビスコースレーヨン | ビスコース | |||||||||
| 木 | 絹 | 木 | 人の皮膚 | カゼイン | |||||||
| 人の皮膚 | ガラス繊維 | アセテート | アセテート人絹 | ||||||||
| 木 | 綿 | 木綿 | ルーサイト | パースペクス | アクリル | ||||||
| Cd Zn Al | アルミ、亜鉛、 カドミウム、 クロム | アルミニウム | ガラス | ポパール | タフノール | オーロン・綿混紡 | |||||
| 紙 | 紙 | 濾紙 | 紙 | 紙 | デクロン | デクロン | パルプ、濾紙 | ||||
| Cr | 絹 | 木綿 | クロム | ||||||||
| 封蝋 | 封蝋 | ||||||||||
| 白蝋 | 樹脂 | エボナイト | エボナイト | エボナイト | |||||||
| 磨かないガラス | 磨いたガラス | 麻 | 酢酸セルロース | ||||||||
| 鉛 | ガラス | ||||||||||
| Fe | 硫黄 | こはく | |||||||||
| Cu Ni | その他の金属 | Fe,Cu,Ag,Pb | 銅、ニッケル、銀真鍮 | 真鍮 | 鋼 | 金属 | |||||
| Ag | 硫黄 | 硫黄 | 硫黄 | ||||||||
| Au | 硬質ゴム | 黒ゴム | |||||||||
| プラチナ | 酢酸人絹 | テリレン(三菱) | |||||||||
| 合成ゴム | ポリスチレン | ビニロン | ポリスチレン | ||||||||
| オーロン | オーロン | オーロン | |||||||||
| (アクリル繊維) | |||||||||||
| サラン | サラン | ||||||||||
| ダイネル | ダクロン | ||||||||||
| ベロン | テリレン | ||||||||||
| カーバイド | |||||||||||
| ポリエチレン | ポリエチレン | ポリエチレン | ポリエチレン | ポリエチレン | ポリエチレン | ||||||
| カネカロン | |||||||||||
| セルロイド | セルロイド | ||||||||||
| インドゴム | インドゴム | セロファン | |||||||||
| 塩化ビニル、ラビロ | |||||||||||
| テフロン | テフロン | テフロン | テフロン | ||||||||
| 酢酸セルロース | |||||||||||
| (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) |
| 1759 Wilche | 1840 Faraday | 1891 Jamin, Bouty's "Physique" | 1917 Shaw |
1924 Silsbee | 1949 Lehmicke | 1954 Ballou | 1955 Hersh, Montogomery |
1957 Rose, Ward | 1958 北川徹三 | 1958 Fukada, Fowler |
物質表面では、クーロン力もファンデルワース力も平衡していませんから、 他の分子が近付くと容易に吸着します。 空気中で最も吸着されやすいのは、酸素と水分ですが、水分の場合、 酸素分子が物体に吸着し、2個の水素分子が空中に向くという結合が多いようです。 このような状態では、水素イオンと OH イオンが高い導電性を持ちますから、 表面状態は、湿度によって大きく変わります。 例えば、1953 年にW.F.Cooperが発表したガラスの表面抵抗を見ると、 この点がよくわかると思います。
| 相対湿度 (%) | 表面抵抗(相対値) |
|---|---|
| 100 | 1 |
| 80 | 4 |
| 70 | 30 |
| 60 | 800 |
| 50 | 30000 |
| 40 | 6000000 |
プラスチックの場合はガラスと違って、材料内部にまで吸着しますが、 電気伝導については、ほぼ同じ結果になって、 このような縁面伝導では、水分子が流動できない程度の薄さで、
log(i/i0) = k*t ここに、 i = 吸着のあるときの電流 i0 = 吸着のないときの電流 k = 定数 t = 吸着層の厚さといった関係が認められています。 電線の場合も、一般に、絶縁体の体積抵抗に比べて、表面抵抗が小さく、 体積抵抗を測定する場合は、表面抵抗を分離するための、 ガード電極が必要です。
簡単な回路ですが、過渡現象の計算は多少面倒で、下記のようになります。
2図の回路で
Qp/Cp = -i1*Rs (a) Qp/Cp = (i2+i3)*Rv+Ql/Cl (b) Ql/Cl = I3*Rl (c) (d/dt)Qp = -(i1+i2+i3) (d) (d/dt)Ql = i2 (e)直接 i3 を求めるのはたいへんですから、最初に Ql を求めることにして、 まず、(b), (c), (e) から i2, i3 を消去して、両辺を微分すれば、
(d/dt)Qp = Cp*Rv*(d/dt)^2(Ql)+(Cp*Rv+Cp*Rl)/Cl/Rl*(d/dt)Ql (f)後はm(a), (b), (c), (d), (e), (f) から、まず Qp と (d/dt)Qp を消去し、 ついで、i1, i2, i3 を消去すれば、次ぎの微分方程式が得られます。
(d/dt)^2(Ql)+(1/Cl/Rl+1/Cl/Rv+1/Cp/Rs+1/Cp/Rv)*(d/dt)(Ql) +1/Cp/Cl*(1/Rp/Cp+1/Rv/Rs+1/Rv/Rl)*Ql = 0 (g)これは線形同次方程式ですから、一般解は、
Ql = Q1*exp(a1*t)+Q2*exp(a2*t) (h) ここに、 a1 = -β+γ a2 = -β-γ β = (1/CP/Rl+1/Cl/Rv+1/Cp/Rs+1/Cp/Rv)/2 γ = sqrt((β^2-4/Cp/Cl*(1/Rl/RS+1/Rv/Rs+1/Rv/Rl))/2
後は初期条件を使って Q1, Q2 を求めるだけですが、初期条件
Qp = Qp (t = 0) Ql = 0 (t = 0)は、このままでは適用できません。そこで、 初期条件というのは回路急変直後の値であることに注意して、 まず、(h) の両辺w微分して、i2 = (d/dt)(Ql) に注意すれば、
i2 = Q1*a1*exp(a1*t)+Q2*2*exp(a2*t) (h2)t = 0 で Qp = Qp の初期条件は t = 0 で I2 = Qp/Cp/Rv と等価ですから、 (g), (h2) にこれら2つの条件を代入すると、
Q1 + Q2 = 0 Qp/Cp/Rv = Q1*a1_Q2*a2 = 0が得られます。この2つの連立方程式を解いて、(g) に代入すれば、
e = Qp/Cp/Cl/Rv*(exp(a1*t)-exp(a2*t))/(a1-a2) (i)
これだけでも、衝撃波になることはわかりますが、
(exp(a1*t)-exp(a2*t))/(a1-a2) = exp*(-β*t)/γ*sinh(γ*t)に注意すれば、
e = (2*Qp*Rl*Rs*exp(-β*t)*sinh(γ*t)) /sqrt((Cp*Rv*Rs+Cl*Rv*Rl+Cp*Rl*Rs+Cl*Rl*Rs)^2 -4*Cp*Cl*Rv*Rl*Rs*(Rv+Rl+Rs)) (j)が得られます。
次ぎに、e の波高値を求めるわけですが、これは、 (j) の右辺を微分して 0 と置けば、
coth(γ*t0) = β/γ (k)ここで、
sinh(γ*t0) = 1/sqrt((coth(γ*t0))^2-1) = γ/sqrt(β^2-γ^2)に注意すれば、
sinh(γ*t0) = sqrt((Cp*Rv*Rs+Cp*Rl*Rs+Cl*Rv*Rl+Cl*Rl*Rs)^2 /(Cp*Cl*Rv*Rl*Rs*(Rv+Rl+Rs))-4)/2 (l)あとは exp(β*t0) を計算すれば終りですが、(k) 式から、
β*t0 = β/γ*atanh(γ/β) ここで、 γ/β = sqrt(1-4*Cp*Cl*Rv*Rl*Rs*(Rv+Rl+Rs) /(Cp*Rv*Rs+Cp*Rl*Rs+Cl*Rv*Rl+Cl*Rl*Rs)^2)ここで、パラメータ a を次ぎのように定義すると、見通しが良くなります。
a = 4*Cp*Cl*Rv*Rl*Rs*(Rv+Rl+Rs) /(Cp*Rv*Rs+Cp*Rl*Rs+Cl*Rv*Rl+Cl*Rl*Rs)^2 (m)まず、a の分母から分子を引いて見れば、常に正になりますから、
0 <= a < 1です。
この a を使って、
exp(-β*t0) = f(a)とすれば、f(a) は a だけの関数となり、
f(a) = exp(-1/2/sqrt(1-a)*log((1+sqrt(1+a))/(1-sqrt(1-a))) (n)あとは、(l), (n) を (j) に代入すれば、
max(e) = Qp*f(a)*sqrt(Rl*Rs/(Cp*Cl*(Rv+Rl+Rs)) (o)となって、(5) 式が得られます。
この種の計算をSpiceで行う場合は、キャパシタの初期値の指定ICと、 過渡解析(transient analysis)のコマンドTARNに UICオプションが必要で、マニュアルを読むとわかるのですが、 市販の文献には書かれていないようですから、 計算例を付けておきます。
microphinocs Rs 2 0 10000M Rv 2 1 1000M Rl 1 0 100M Cp 2 0 100P IC=1V Cl 1 0 1000P .CONTROL tran 0S 1000PS uic plot V(1) .ENDC .END
以上は 1973-04-25 に書いた技術資料 「ワイヤのマイクロフォニック雑音概論」の要約です。
平林 浩一, 2006