注５ - (6), (7) 式の根拠

塑性疲労による断線は曲率最大の場所で生じますから、 試料が 90 度曲げられたときの、曲率の最大値を求めればよいわけですが、 試料がピアノ線のような弾性体で近似できる場合を考えます。

この場合、機械工学の材料力学や土木工学の構造力学の たわみを使った近似が使えませんから、 微分幾何学の自然方程式を使うことになりますが、 この問題については曲率を直接扱うため、 デカルト座標を使うより簡単になります。

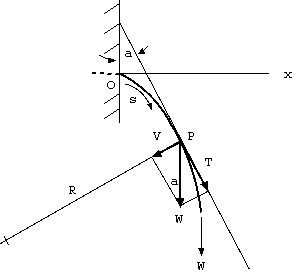
  O = 固定ガイド端(試料可動部の始端)
  s = O を原点とした試料中心軸の弧の長さ
  a = 試料試料中心軸の P に於ける接線と垂直軸の角度 (0 <= a <= π/2)
  R = 試料試料中心軸の P に於ける曲率半径
  V = 試料試料中心軸の P に於ける剪断力
  T = 試料試料中心軸の P に於ける張力
  W = O から十分離れた場所に加えた下向き加重

１図のように、固定ガイド端を O として、O から水平に保持された試料に、 O から十分離れた場所に試料中心と直行する方向の加重 W を加えた状態を考えると、 試料に加わる剪断力は、

  V = W * sin(a)                                               (1)
  sin(a) = dx / ds                                             (2)

一方、試料の曲げ剛性、せん断力、曲げモーメントの基本的関係は、

  (d/ds)(M) = V                                                (3)
  1 / R  = M / B                                               (4)
  ここに、
	M = 曲げモーメント
	V = せん断力
	B = 曲げ剛性
	R = 曲率半径

  (d/ds)(1/R) = (d/ds)(M) / B
              = V / B
              = W / B * sin(a)                                  (5)

  ds = R * da                                                 (6)

  (d/da)(1 / R^2) = W / B * sin(a)                              (7)

                       t
  1 / R^2 = (W / B) * ∫sin(a)*da
                      0
          = (W / B) * (1 - cos(t))  (0 <= t <= π/2)            (8)

曲率半径の最小値は t = π/2、すなわち、試料と保持具の接点で、

  1 / R^2 = W / B                                               (9)

破断繰返数は最小曲率半径の自乗に反比例しますから、 定加重折曲げ疲労試験に於いては 破断繰返数は加重に反比例することがわかります。

なお、折曲げ角度が +-90 度より小さい場合も、 (8) 式の t が折曲げ角度になりますから、 この定性的関係は変わりません。