リード線のインダクタンスという誤解

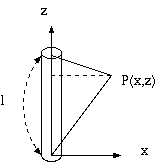
円形断面の リード線のインダクタンスと称する下記の公式が無数の文献に出てきます。

  L = μ * l / (2 * π) * (log(2 * l / a) - 1)                          (1)
  ここに、
	L = リード線のインダクタンス (H)
	l = リード線の長さ (m)
	a = リード線の半径 (m)
	μ = 透磁率 (H/m)
	   = μ0 * μs
	μ0 = 4-7 * π (H/m)
	μs = 比透磁率 (銅などの非磁性体ではほぼ 1.0)
	π = 3.1415..

この式の面白いところは、インダクタンスがリード線の長さに比例しないことで、もし、これが正しいとすると、例えば、

  l = a * e / 2
  ここに、
	e = 2.71828459.. (自然対数の底)

の場合なら L = 0 になるとか、

  l < a * e / 2

なら、インダクタンスが負になるとか、さらには、長さが長くなるにつれて単位長あたりインダクタンス L/l が無限大に発散するとか、少し考えれば、この式がおかしいことはすぐわかるはずですが、文部省の日の丸と君が代がすべてという思考力を奪う教育システムが成功したためか、この式が氾濫しています。 (IEEE 規格など、日本以外でも見掛けます。)

この式を得る方法としては、単独円筒形導体に流れる電流による磁束を積分する方法(注１)とか、電磁気学の偉人Maxwell由来の 幾何学的平均距離(geometiric mean distance)を使う方法がありますが、後者の場合なら、

  L = μ * l / (2 * π) * (log(2 * l / R) - 1)                          (2)
  ここに、
	R = 幾何学的平均距離 (m)
	  = a                                .. 円筒自身の幾何学的平均距離
	  = a * exp(-1/4)                    .. 円柱自身の幾何学的平均距離
	  = log(a) + log(2)/3 + π/3 - 25/12 .. 正方形柱自身の幾何学的平均距離
	  ..
	a = 円筒、円柱の半径、正方形柱の辺の長さ (m)

から、(1) 式が円筒、すなわち、円柱表面だけに電荷が存在する状況を考えていることがわかります。

何故、この式から異様な結果が得られるかというと、本来、インダクタンスは回路について定義されるものであって、回路の一部でしかないリート線のインダクタンスは意味をもたないことを忘れてしまったためです。

リード線を回路にするためには、 戻りの導体が不可欠で、もっとも単純な平行往復導体の自己インダクタンスを考えると、次ぎのようになります。(注２)

  L = μ * l / (4 * π) * (4 * log(R12) - 2 * log(R11) - 2 * log(R22))   (3)
  ここに、
	L = 平行往復導体回路の自己インダクタンス (H)
	R12 = 導体 1 と導体 2 の間の幾何学的平均距離 (m)
	R11 = 導体 1 自身の幾何学的平均距離 (m)
	R22 = 導体 2 自身の幾何学的平均距離

円柱導体について具体的に計算してみると、平衡往復導体の長さが十分長ければ、

  log(R12) = 2 * log(2 * l) - 1
	- (log((l + sqrt((l^2  + d^2)) / d)) - sqrt(l^2  + d^2) + d)
      ～ log(d)   (d << l)
  ここに、
	d = 導体中心間距離 (m)

ですから、

  R12 = R21 = d

また、

  R11 = R22 = e * exp(-1/4)

ですから、

  L = μ * l / π * (log d / a) + 1 / 4)                          (4)

と、単位長あたりのインダクタンス L/l は一定になります。

結局、(1) 式はインダクタンスを求める一周積分の一部だけを計算したもので、完全な計算ではなかったわけです。

(1), (2) 式では宇宙に有限長のリード線が 1 本だけ単独に存在し、そこに直流電流が流れている不自然な状況を考えていますから、リード線外部には無限遠に広がる磁束が存在することになりますが、戻りの導体があれば、この磁束のかなりの部分が打ち消されて減少しますので、 (1) 式の異様な結果を生む log() の中の l が消えてしまいます。

注

注１ - 錯交磁束を積分する方法

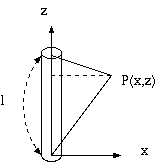
P 点に於ける磁界は

  H = (I/(4*π*x)*(z/sqrt(x^2+z^2) + (l - z)/sqrt(x^2 + (l - z)^2))
  ここに、
	H = P(x,z) 点の磁界強度 (AT/m)
	l = 導体の長さ (m)

ですから、外部磁界のリード線との錯交磁束は

  Φ = μ*I/(4*π)*∫∫μ*H*dx*dz

                   ∽  l
     = μ*I/(4*π)*∫ ∫ (1/z)*(z/sqrt(x^2 + z^2) + (l - z)/sqrt(x^2 + (l - z)^2) dz*dx
                   a  0
     = μ*I/(2*π)*{l*log((l + sqrt(a^2 + l^2)/a) - sqrt(a^2 + l^2) + a)
  ここに、
	Φ = 錯交磁束 (weber)
	a = 導体半径 (m)

導体外部の磁界のうち、x 軸方向は導体表面から無限遠まで、 z 軸方向は導体端部間のみ積分していることに注意してください。空間全体としては、 x 軸方向は戻りの導体があれば過大評価になりますし、 z 軸方向は過小評価になります。

この積分範囲であれば、外部インダクタンスは

  Le = Φ/I
     = μ/(2*π)*(l*log((l + sqrt(a^2 + l^2)/a) - sqrt(a^2 + l^2) + a)
     = μ/(2*π)*(log(2*l/a) - 1)  (a << l)

となって、(1) 式が得られます。

注２ - インダクタンスの直列接続

回路的に見ると、 (3) 式

  L = μ * l / (4 * π) * (4 * log(R12) - 2 * log(R11) - 2 * log(R22))  (H)

を導体の自己インダクタンスと相互インダクタンスに書き換えて、

  L = L1 + L2 - 2 * M
  ここに、
	L = 平行往復導体のインダクタンス (H)
	L1 = 導体 1 の自己インダクタンス (H)
	L2 = 導体 2 の自己インダクタンス (H)
	M = 導体 1 と導体 2 の相互インダクタンス (H)

つまり、回路的には、二つの導体を流れる電流が逆向きですから、自己インダクタンス L1 と L2 の直列逆接続になります。

具体的に計算してみると、

  L1 = L2 = μ*l/(2*π)*(log(2*l/d - 1)
  M = μ*l/(2*π)*(log(2*l/d - 1)

ですから、

  L = L1 + L2 - 2 * M
    = μ*l/π*(log(d/a + 1/4)

と、問題だった log() の中の l が消えてしまいます。

つまり、(1) 式は回路の一部でしかない L1 だけを見ていて、それが回路全体のインダクタンスだと早トチリしたのがおかしな結論を生む理由でした。

平林浩一, 2014-07