カテナリー曲線 (懸垂線)

ロープ、紐、電線、鎖などの両端を持ったときにできる曲線は Catenaryと呼ばれますが、 Catenary の用語はラテン語の catena (鎖) に起因するもので、 名付け親は Christiaan Huygens だそうです。 15 世紀のチベットの仏僧Thang Tong Gyalpoは鉄の鎖を使った巨大な吊橋を たくさん作りました。(注１)

この曲線が簡単な双曲線関数で表せることは、下記のようにして確認できます。 (注２)

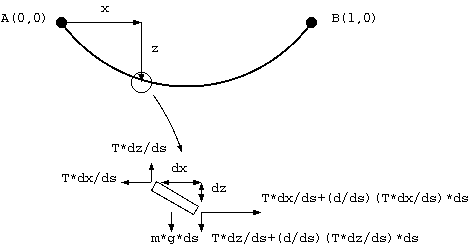
１図 カテナリー曲線

１図に於いて垂直方向の力の平衡条件は

  (d/ds)(T * dz/ds) = -m * g                                (1)
  ここに、
	T = ロープの張力
	m = ロープの単位長あたり質量
	g = 重力加速度

  (s/ds)(T * dx/ds) = 0                                     (2)

  T * dx/ds = H                                             (3)
  ここに、
	H = 水平方向張力 (定数)

(3) を (1) に代入して、

  H * (d/dx)^2(z) = -m * g * ds/dx                          (4)

  (dx/ds)^2 + (dz/ds)^2 = 1                                 (5)

  H * (d/dx)^2 = -m * g * sqrt(1 + (dz/dx)^2)               (6)

あとは、これを解けば良いのですが、指数関数の拡張である双曲線関数の性質 (注３)

  (cosh(t))^2 - (sinh*t))^2 = 1
  (d/dt)(cosh(t)) = sinh(t)
  (d/dt)(sinh(t)) = cosh(t)

  z = H/(m*g) * (cosh(m*g*(l/2)/H) - cosh(m*g/H*(l/2 - x))   (7)

x = 0 から x までのロープの長さ s は

       x
  s = ∫sqrt(1 + (dz/dx)^2)*dx
      0
    = H/(m*g)*(sinh(m*g*(l/2)/H) - sinh(m*g/H*(l/2 - x))

  sinh(m*g*(l/2)/H = m*g*(L0/2)/H                            (8)
  ここに、
	L0 = ロープの全長

ロープの張力は場所によって変化し、次のようになります。

  T = H * cosh(m*g/H*(l/2 - x)                               (9)
  ここに、
	T = ロープの張力

ロープをどんどん長くしていって、1 << m*g*/2/H になれば、張力は m*g*L0/2 になって、ロープ全体の目方と一致します。

ロープ最下端までの深さは x = l/2 に於ける z の値

  zmax = H/(m*g) * (cosh(m*g*(l/2)/H) - 1)

ロープの形状はスパン l、水平張力 H、ロープの全長 L0 のうち、 いずれか 2 つが決まれば確定しますが、 工学的には、H を小さくすると張力が減る一方、 たるみが大きくなって、 架空送電線では振動事故とか地上物体との衝突の危険が増えます。 逆に H を増やすと張力が増加して、 ロープの強度が不足します。

また、ロープ最下端の曲率半径

  r = (1 + (dz/dx)^2)^(3/2) / (d/dx)^2(z)
    = H/(m*g)
  ここに、
	r = 曲率半径

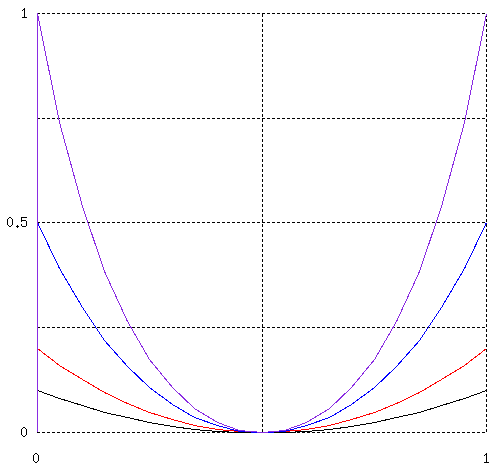
２図 カテナリー低部の曲率

なお、架空送電線の設計では cosh() を使わずに、2 次関数近似で済ませていまが、 理由は m*g*l/H << 1 の条件で施工されるためで、 cosh(x) の級数展開

  cosh(x) = 1 + x^2/2! + x^4/4! + ..

なお、ここではロープの両端が同じ高さの場合を扱いましたが、 高さが違ってもやはり双曲線関数 cosh(x) の一部になります。

注１ - Thang Tong Gyalpo

15 世紀のチベットの僧 Thang Tong Gyalpo は医術、鍛冶、建築の仕事に加えて、土木工学の創始者でもあって、 チベットとブータンに 58 もの鉄鎖吊橋を作ったと伝えられていますが、 その建設費用の捻出を目的に 7 人の女性を選抜して創作公演した フォーク・オペラ は今も引き継がれているそうです。

注２ - 変分法

  s = ∫sqrt(((d/dx)(f(x))^2 + 1)*dx

  H = ∫f(x)*sqrt((d/dx)(f(x))^2 + 1)*dx

注３ - 双曲線関数

  sinh(x) = (exp(x) - exp(-x)) / 2
  cosh(x) = (exp(x) + exp(-x)) / 2
  tanh(x) = (exp(x) - exp(-x)) / (exp(x) - exp(-x))
  asinh(x) = log(x + sqrt(x^2 + 1))
  acash(x) = log(x + sqrt(x^2 - 1))
  atanh(x) = log((1 + x) / (1 - x)) / 2