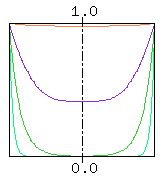
Fig. 1 Skin effect for annealed copper wire with a diameter of 1mm
Current flowing through a cylindrical conductor distributes evenly along the conductor cross-section when the current is a direct current. However, with the increase in frequency, the effect where the current concentrates at the conductor surface and the current density decreases at the center, is known well as the skin effect (footnote 1).
For example, Fig. 1 shows the current density in the conductor cross-section of an annealed copper wire with a diameter of 1mm for frequencies 10kHz, 100kHz, 1MHz and 10MHz.

Fig. 1 Skin effect for annealed copper wire with a diameter of 1mm
The x-axis in Fig. 1 is the distance from the conductor center (center of the figure represents the center of the conductor and both ends show the conductor surface), and the y-axis is (internal current density/current density at conductor surface).
The red, purple, green and light green lines correspond to the current density in the conductor cross-section for 10kHz, 100kHz, 1MHz and 10MHz respectively. The current density at the center of the conductor decreases from 98% of the surface for 10kHz, to 41% for 100kHz, to 0.4% for 1MHz, and to just 0.00000006 % for 10 MHz.
As a result of the skin effect, the effective cross-section of the conductor decreases and alternating current resistance increases. Therefore, in coil windings, conductor loss increases and the "Q" (quality factor), or quality, decreases with the increase in frequency.
As a countermeasure, from early times "Litz wire" was used for bar antenna coils in shortwave radios and mid-frequency transformer windings. Litz wire is many thin insulated conductor strands twisted together.
Many people considered applying the concept behind Litz wire to "audio cables",
and came up with the idea as shown in Fig. 2.
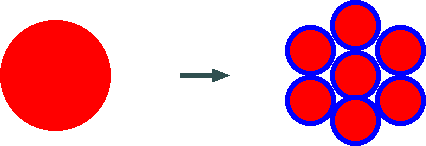
Fig. 2 Splitting a single wire conductor into many insulated conductors
(conductors in red, insulators in blue)
Here, we split a single wire conductor into many insulated conductors with the same conductor cross-section area. For example, if we split into seven wires, we get the configuration shown in Fig. 2. People who think of these products think that "if we increase the number of wires, we can make a cable with less skin effect. If company A has a product with 19 wires, we make one with 30 wires. If they beat us, we will increase the number of wires by one...".
As a consequence, many audio cables with Litz wire were born. Is this strategy effective?
This is the question.
Obtaining the current distribution of a single cylindrical conductor under high frequency is relatively simple, and the solution is shown below. The current distribution shown in Fig. 1 has been calculated using this equation. However, only the magnitude is shown. Note that the phase of the current also depends on the position. As we get deeper into the conductor from the surface, the phase of the current delays and may even become backward!
Ir / Ia = I0(sqrt(j)*k*r) / I0(sqrt(j)*k*a) Here, Ir = current density (A/m^2) at radius r (m) Ia = current density at outer surface of conductor (A/m^2) a = conductor radius (m) j = sqrt(-1) k = sqrt(w*u*g) w = angular velocity (rad/s) = 2*PI*f PI = 3.14159265.. f = frequency (Hz) u = permeability (H/m) g = dielectric constant (S/m) I0(z) = Modified Bessel Function of First kind of order 0 I1(z) = Modified Bessel Function of First kind of order 1The first mathematical discussions on the skin effect of wires were done by Maxwell, who started modern electromagnetics in 1873. This was followed by significant contributions by the creative genius Heaviside, who followed the theoretical work of Maxwell in 1884-1887, and by Poynting in 1884-1885. Experimental confirmation was first done by Hughes in 1886. Numerical engineering calculations on the applicable level was first done by Lord Rayleigh for the skin effect on infinite planes in 1886, and on cylindrical conductors by Lord Kelvin using ber-bei functions in 1899. Afterwards, there was work by Hertz and J.J. Thomson, who took over experimental work by Maxwell. The first person to use the word "skin effect" is considered to be J.Swinburne in 1891. Until recently, there were continuous challenges by many brilliant theorists and engineers, including H.B.Dwight and A.E.Kennelly.
For your information, the word "Litz wire" comes from the German word "Litzendraht" (twisted strands).
Kouichi Hirabayashi, (C) 2003