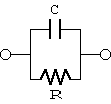
 Fig. 1. Parallel equivalent circuit of capacitors
Fig. 1. Parallel equivalent circuit of capacitors
Capacitance is the ability to store electrostatic energy and always exists between conductors. Therefore, capacitance is the second most important electric property after conductor resistance. For example, in the polyethylene-insulated coaxial cable "3C-2V" (JIS C 3501), capacitance is regulated as 67+-3 pF/m (1 kHz).
Capacitance is determined by the geometrical configuration of the conductor and dielectric nd, the dielectric constant of the dielectric. In turn, the dielectric constant is determined by the dipole moment as a result of the positive and negative charges in atoms, molecules and crystals being displaced from their average positions by an external electric field. The displacement changes with frequency and temperature, and therefore the dielectric constant usually has a frequency dependence.
 Fig. 1. Parallel equivalent circuit of capacitors
Fig. 1. Parallel equivalent circuit of capacitors
The following is an actual measurement of a frequency dependence on capacitance of the coaxial cable described above. We used our low frequency impedance measurement device for measurement. The sample length was 1m, and the parallel equivalent circuit shown in Fig. 1 was selected as the impedance measurement model. Good quality capacitors fit this model well.
| Frequency (MHz) | ?Capacitance (pF) | D | ||
|---|---|---|---|---|
| 1 | 67.2 | 0.0000 | ||
| 2 | 67.3 | 0.0000 | ||
| 3 | 67.4 | 0.0000 | ||
| 4 | 67.5 | 0.0000 | ||
| 5 | 67.7 | 0.0000 | ||
| 6 | 68.0 | 0.0000 | ||
| 7 | 68.3 | 0.0005 | ||
| 8 | 68.7 | 0.0011 | ||
| 9 | 69.1 | 0.0019 | ||
| 10 | 69.5 | 0.0024 | ||
| 11 | 70.0 | 0.0032 | ||
| 12 | 70.6 | 0.0046 | ||
| 13 | 71.2 | 0.0050 |
In the model shown in Fig. 1, "D" is defined as
D = R/(w*C) . Here, D = Dielectric loss w = Angular frequency (rad/s) = 2*PI*f PI = 3.14159265.. f = frequency (Hz) C = Capacitance (F) R = Parallel resistance (Ohm)
This is proportional to the loss divided by energy stored and is an indication of energy storage efficiency. For capacitors, this indicates the ratio of loss by the dielectric. (footnote 1)
The question is, can we deduce from the measurement data that the "capacitance of a polyethylene-insulated coaxial cable (dielectric constant of polyethylene) and conductance (dielectric loss from polyethylene) increase with frequency (above around 10 MHz")? In other words, is the above measurement data showing the frequency dependence on capacitance and dielectric loss?
When an alternating voltage V is applied to both ends of the capacitor in Fig. 1,
D = R/(w*C)
= 2 * PI * (R*V^2/f) / (C*V^2)
= 2 * PI * (energy_lost_per_1_Hz) / stored_energy.
There is a convention to write D as tan(delta). This is because when the total
current flowing through the capacitor is considered as a vector sum of current
Ic flowing through C and Ir flowing through R, the angle between these two
vectors is delta.
In electronic parts that store energy, parts with a small D is good, but for
inductors (coils), we define the inverse of D as Q and consider that parts
with high Q have high quality.
Kouichi Hirabayashi, (C) 2001