
Fig. 1 Solenoid coil

Fig. 1 Solenoid coil
Magnet wires are a type of wire that is used as electromagnets and coils. The simplest application is the solenoid coil shown in Fig. 1. The intrinsic setup of a coil is a closely wound conductor, and the conductor is covered by a thin and strong film.
The approximate high-frequency resistance and inductance of a solenoid coil, under the condition that the coil length is longer than the coil radius, is known as
Rhf = 2*PI*a/b*n^2*R1 (1) L = u0*PI*a^2*n^2/(b + 0.9*a) (2) Here, Rhf = High-frequency resistance (Ohm) L = Inductance (H) PI = 3.14159265.. a = Coil radius (m) b = Coil length (m) n = Turns in coil (turn) R1 = sqrt(PI*f*u/g) f = Frequency (Hz) u = Permeability of conductor (H/m) u0 = Permeability of air (H/m) g = Conductivity (mho/m)R1 is the effective resistance based on a voltage drop from the surface when a high frequency current passes through an infinite plane conductor, and is a conductor dependent value called surface resistivity or intrinsic resistance. Note that this value depends only on the material properties and is independent of the geometrical configurations. This is because regardless of the thickness of the plate, the skin effect limits most of the current to a certain depth below the surface determined by the conductivity, permeability and frequency.
Some people may feel that a plane with an infinite width may be unnatural; however, infinite planes are very common, basic structures. For example, tubes and surfaces of cylinders are intrinsically infinite planes (there is no edge in the tangential direction!), and sections of smooth conductor surfaces on an electromagnetic wave wavelength scale.
In this case, currents concentrate on the inner surface and outer surface of the coil because high frequency currents can only exist on the surface of the strands due to the skin effect, and proximity effects decrease the currents' density close to the adjacent strands.
Therefore, decreasing proximity effects by slightly reducing the conductor radius compared to the winding pitch, the current starts to flow not only at the inner and outer surfaces of the coil, but also at the gaps between conductors, and reduction of alternating current resistance exceeding the increase of direct current resistance can be obtained. However, decreasing the conductor radius too much will result in an extreme increase in the direct current resistance and will result in the decrease of properties. Thus, it is clear that there is an optimum value. People who have wound coils for shortwave radio receivers during childhood may remember sparsely winding to make gaps between strands.
It is common to evaluate the quality factor of coils as the ratio between reactance and resistance
Q = w*L/Rhf (3) where Q = Quality Factor w = 2*PI*f PI = 3.14159265.. f = frequency (Hz)because the purpose of coils is to store magnetic energy. The above equation also means
Q = 2*PI*stored_energy / energy_consumed_per_cycle
For coils with non-magnetic conductors such as copper and aluminum, the above results yield the following equation.
Q = a/d/(1 + 0.9*a/b) (4)
Here
d = sqrt (2/(w*u*g))
Q = Quality of coil
= power_consumed_by_coil / power_stored_by_coil.
d is the skin depth, which is a good guide to determine the effects of the
skin effect, and is useful to simplify equations related to the skin effect.
Coils are often shielded to prevent interference with other circuits, and here we use a cylindrical shield as shown in Fig. 2.
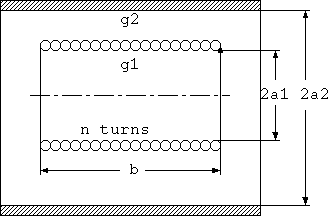
Fig.2. Solenoid coil in cylindrical shield.
The current now flows inside the shield in addition to the inside and outside layers of the conductor; therefore energy loss happens inside the shield, and not just in the conductor.
The effective resistance of the coil will be affected by the shield, and the question is whether the "Rhf" in equation (1) will increase, decrease, or not change compared to when there is no shield.
Kouichi Hirabayashi, (C) 2000