Mystery about Pulse Transmission Distance - EIA-422
In pulse transmission by cable, the longer the distant is, the more
difficult it is to transmit pulse quickly. For example, in the appendix of
"RS-422-A," it is recommended to use a figure as shown below as
conservative guide of selection;
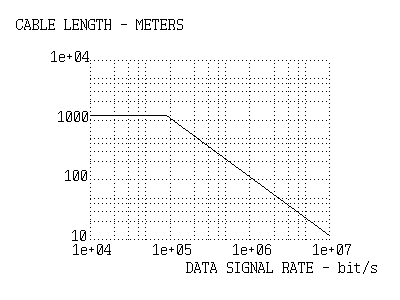
Then, it is honestly confessed that, in this standard, this figure is based
upon empirical data and has been made from the following criteria, where
telephone cable of copper conductor (24 AWG, 52.5pF/m) terminated at the
resistance of 100 Ohm is used;
a. Rise and fall times of pulse are the half of pulse width,
b. Voltage fall from signal to load is below 6dB.
The criterion of being up to the half of pulse width may be acceptable,
since "slow speed of rise and fall is good enough as long as they catch up
with speed of pulse." Meanwhile, they have left no doubt about that
"voltage fall up to the half may be acceptable" by judgment in a
traditional way of the electric engineering field. The Supreme Court of
Japan has made a precedent that two constituencies are equal even if one of
them has more than twice as many voters as the other. In the field of
engineering, however, there is a tradition that they do not regard two
things equal if their proportion is bigger than 1:2, which everybody except
lawyers may think appropriate.
Now, regarding theoretical bases of the above figure, it is easy to imagine
that the limit of the cable length, which is "constant" up to 1.2 km at the
transmission speed of less than 90 kpbs, is caused by direct current
resistance. That is because this straight line "is stretched up to direct
current."
Let's confirm this by calculation here. Direct current resistance of 24 AWG
copper conductor is 0.0842 Ohm/m, which is doubled in a round-trip.
Meanwhile, the impedance of the transmitter and the receiver is 100 Ohm
respectively. Also, the input voltage of the receiver falls to 1/2 in
direct current, when the direct current resistance of the cable reaches 200
Ohm. Since this point is set as the limit of the cable length, the formula
of;
the limit of the cable length = 200/(0.0842*2) = 1200 m (1)
corresponds to the above figure. In other words, this territory is fixed
with the criterion (b).
The matter is the straight line over 90 kbps. The line which is based on
the criterion (a) shows that it becomes difficult more and more to make
rapid transmission with long cables, because the longer the cable is, the
slower the waveform of pulse is to rise or fall. The figure shows that
experiments with cables of different length have revealed the above result.
However, as experimental data, such relation of inverse proportion as;
the limit of cable length = 1.2 e8 / s(m) (2)
where, s = transmission speed (bit/s)
looks so neat that it suggests that "there is somewhat simple and strong
theoretical basis." In other words, it does not seem to be a mere
experimental or empirical law.
Besides, a defect of experimental data is their lacking generality. For
example, this standard shows only the data about one kind of electric
cable, 24 AWG telephone cable, but does not show;
1) how they are with cables of different sizes,
2) how they are with other structures.
Therefore, it is quite dubious as an index of selection.
Is a relation like (2) really explainable only experimentally or
empirically? Do we have to give up pursuit of theoretical bases, like the
author of "EIA-422-A" and many other writers who have referred to or
requoted this guideline, and to shelter ourselves in an uncomfortable
"empirical" world?
This is the question this time. Introducing this kind of writing is a good
aspect of US standards, that does not happen with Japanese standards.
Japanese standards are somewhat useless on principles of too much favor to
influence exerted from the authority and of too much memory work, which is
most likely in a bureaucratic country.
(Note) The same kind of experimental data can be found in the standard of
"EIA-423-A" and in some books such as "Computer Data Communication
Technology" by John E. MacNamara (CQ Publishing).
return to home
