[Answer] When power source current is "i1," current in capacitor "i2," curre nt in inductance "i3," the formulae found are the following three;
In the 396th page of a book titled "Electric Theory Exercise III" that has been published many years ago by Ohm-sha, there is an exercise as follows. Please understand that differential signs are not easy to read here, since I have written the exercise with JIS Kanji Code that does not get along with science and engineering.
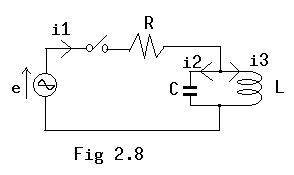
[Exercise 6] In the circuit of figure 2.8, when parallel circuits "L" and
"C" resonate to power source frequency, please find the transient current
"i" for adding alternating current voltage, "e=E*cos(omega*t),"
whereas, t=0. All the initial values are zero, here.

[Answer] When power source current is "i1," current in capacitor "i2," curre
nt in inductance "i3," the formulae found are the following three;
i1 = i2 + i3 (1) R*i1 + L*(d(i3)/dt) = E*cos(omega*t) (2) L*(d(i3)/dt) = (1/C)*Integral(i2)*dt (3)From the formula (3), L*(d^2(i3)/dt^2) = i2/C and, from the meaning of the subject, omega=1/sqrt(L*C) . Therefore,
i2 = (1/omega^2)*(d^2(i2)/dt^2) (4)From the formula (2),
d(i2)/dt = (E/L)*cos(omega*t) - (R/L)*i1 (5)By differentiating the above with t,
d^2(i3)/dt^2 = -(E/L)*omega*sin(omega*t) - (R/L)*d(i1)/dtBy substituting this for the formula (4),
i2 = -(E/(omega*L))*sin(omega*t) - (R/(omega^2*L))*d(i1)/dt (6)By integrating the formula (5) with "t,"
i3 = (E/(omega*L))*sin(omega*t) - (R/L)*Integral(i1)*dt (7)From the formulae (6) and (7),
i1 = -(E/(omega*L))*sin(omega*t) - (R/(omega^2*L))*d(i1)/dt
+ (R/(omega*L))*sin(omega*t) - (R/L)*Integral(i1)*dt
= -(R/(omega^2*L))*d(i1)/dt - (R/L)*Integral(i1)*dt
Therefore,
(R/((omega^2*L))*d(i1)/dt^2 + i1 + (R/L)*Integral(i1)*dt = 0
By differentiating this with "t,"
(R/(omega^2*L))*(d^2(i1)/dt^2) + d(i1)/dt + (R/L)*i1 = 0
The answer to this equation is in the formula of "t=A*exp(g *t)," whereas
"i1=0" can be obtained by substituting initial conditions of "i1=0" when
"t=0." Also, from the formula (6),
i2 = -(E/(omega*L))*sin(omega*t)
and from the formula (1),
i3 = (E/(omega*L))*sin(omega*t)
are obtained. In other words, transient current is not generated.
The above is the exercise and the answer. The key is that L and C are
parallel resonance to the power source of sine waves. It is theoretical
that "i1" becomes zero, since the impedance of L-C parallel circuit becomes
infinite in the alternating current theory that regards the stationary
state as important. However, when it comes to transient state, it does not
seem suitable to have the answer that "i1" becomes constantly zero and the
transient current does not occur.
Suppose the answer is correct, the following question arises;
How can the energy of the currents "i2" and "i3" that have not existed
in the initial state be transferred from the electric source?
Also, as long as "i1" is zero, there is no loss of energy from the electric
source. If so, it is possible with this theory to make an electric stove
that does not require electric power, by giving energy to L-C parallel
circuits and then extracting energy by connecting "R" to L-C parallel
circuits.
That means you can generate energy without any compensation, which is
against the principle of the conservation of energy, the basic of physical
science. But, I assume this exercise is not a groundless writing because
the book has been written by an expert in the field for education in a
specialized course of the electrical engineering department of a
university. So, how can I understand it?